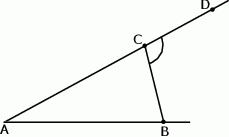
Odcinki 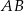 oraz
oraz 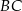 (rysunek) są równej długości. Kąt
(rysunek) są równej długości. Kąt 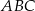 ma miarę o
ma miarę o 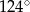 mniejszą od miary kąta do niego przyległego. Oblicz miarę kąta
mniejszą od miary kąta do niego przyległego. Oblicz miarę kąta  .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
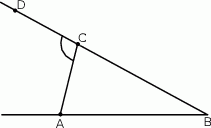
Odcinki  oraz
oraz  (rysunek) są równej długości. Kąt
(rysunek) są równej długości. Kąt 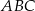 ma miarę o
ma miarę o 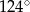 mniejszą od miary kąta do niego przyległego. Oblicz miarę kąta
mniejszą od miary kąta do niego przyległego. Oblicz miarę kąta 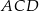 .
.

Odcinki 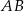 oraz
oraz 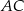 (rysunek) są równej długości. Kąt
(rysunek) są równej długości. Kąt 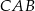 ma miarę o
ma miarę o 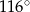 mniejszą od miary kąta do niego przyległego. Oblicz miarę kąta
mniejszą od miary kąta do niego przyległego. Oblicz miarę kąta 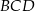 .
.
Wyznacz pole trójkąta równobocznego, którego wysokość jest o 1 cm krótsza od boku tego trójkąta.
Wyznacz pole trójkąta równobocznego, którego wysokość jest o 2 cm krótsza od boku tego trójkąta.
Dany jest trójkąt o bokach długości 7,8,9.
Dane są miary łukowe dwóch kątów trójkąta: 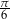 i
i 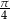 . Wyznacz miarę trzeciego kąta w stopniach i radianach.
. Wyznacz miarę trzeciego kąta w stopniach i radianach.
Dane są miary łukowe dwóch kątów trójkąta: 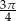 i
i 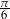 . Wyznacz miarę trzeciego kąta w stopniach i radianach.
. Wyznacz miarę trzeciego kąta w stopniach i radianach.
Dane są miary łukowe dwóch kątów trójkąta: 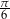 i
i 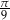 . Wyznacz miarę trzeciego kąta w stopniach i radianach.
. Wyznacz miarę trzeciego kąta w stopniach i radianach.
Dane są miary łukowe dwóch kątów trójkąta: 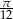 i
i 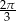 . Wyznacz miarę trzeciego kąta w stopniach i radianach.
. Wyznacz miarę trzeciego kąta w stopniach i radianach.
W trójkącie prostokątnym iloczyn sinusa jednego z kątów ostrych i tangensa drugiego kąta ostrego jest równy 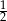 . Oblicz miary kątów ostrych tego trójkąta.
. Oblicz miary kątów ostrych tego trójkąta.
W trójkącie 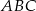 dane są:
dane są: 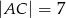 ,
, 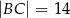 i
i 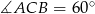 . Oblicz pole trójkąta
. Oblicz pole trójkąta 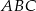 .
.
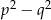 ,
, 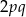 i
i 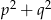 , gdzie
, gdzie 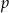 i
i 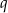 są liczbami dodatnimi takimi, że
są liczbami dodatnimi takimi, że 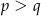 , to trójkąt ten jest prostokątny.
, to trójkąt ten jest prostokątny. 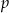 i
i 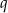 , dla których najkrótszy bok otrzymanego trójkąta ma długość 13.
, dla których najkrótszy bok otrzymanego trójkąta ma długość 13.Na przyprostokątnych 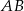 i
i 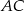 trójkąta prostokątnego równoramiennego
trójkąta prostokątnego równoramiennego 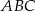 zaznaczono odpowiednio punkty
zaznaczono odpowiednio punkty 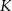 i
i 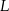 tak, że
tak, że 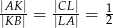 . Odcinki
. Odcinki 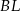 i
i 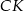 przecinają się w punkcie
przecinają się w punkcie 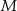 . Oblicz
. Oblicz 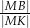 .
.
Udowodnij, że jeżeli środek okręgu opisanego na trójkącie leży na jednym z jego boków, to trójkąt ten jest prostokątny.
Wysokość poprowadzona z wierzchołka kąta prostego trójkąta prostokątnego dzieli przeciwprostokątna na odcinki o długościach 1 i 2. Oblicz długości boków tego trójkąta.
Oblicz sumę długości środkowych trójkąta o długościach boków: 2, 3 i 4.
Na okręgu o promieniu 9 opisano trójkąt równoramienny o kącie równym 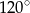 . Oblicz długości boków trójkąta.
. Oblicz długości boków trójkąta.
W trójkącie prostokątnym 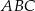 przyprostokątne mają długości:
przyprostokątne mają długości: 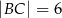 ,
, 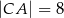 . Na boku
. Na boku 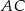 wybrano punkt
wybrano punkt 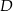 tak, że odcinki
tak, że odcinki 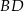 i
i 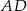 mają równe długości. Oblicz długość odcinka
mają równe długości. Oblicz długość odcinka 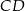 .
.
Dany jest trójkąt o przyprostokątnych 12 i 5. Wyznacz promień okręgu wpisanego w ten trójkąt.
Dany jest trójkąt o przyprostokątnych 24 i 7. Wyznacz promień okręgu wpisanego w ten trójkąt.
Trójkąt 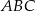 jest prostokątny. Punkt
jest prostokątny. Punkt 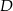 jest spodkiem wysokości opuszczonej na przeciwprostokątną
jest spodkiem wysokości opuszczonej na przeciwprostokątną 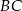 oraz
oraz 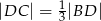 (patrz rysunek). Wykaż, że
(patrz rysunek). Wykaż, że 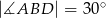 .
.
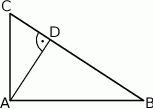
Przez środek okręgu wpisanego w trójkąt równoboczny 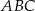 poprowadzono prostą równoległą do boku
poprowadzono prostą równoległą do boku 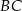 i przecinającą bok
i przecinającą bok 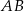 w punkcie
w punkcie 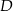 . Oblicz iloraz
. Oblicz iloraz 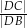 .
.
Trójkąty prostokątne 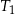 i
i 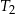 są podobne. Przyprostokątne trójkąta
są podobne. Przyprostokątne trójkąta 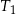 mają długości 5 i 12. Przeciwprostokątna trójkąta
mają długości 5 i 12. Przeciwprostokątna trójkąta 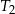 ma długość 26. Oblicz pole trójkąta
ma długość 26. Oblicz pole trójkąta 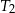 .
.
Trójkąty prostokątne 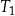 i
i 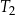 są podobne. Przyprostokątne trójkąta
są podobne. Przyprostokątne trójkąta 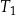 mają długości 7 i 24. Przeciwprostokątna trójkąta
mają długości 7 i 24. Przeciwprostokątna trójkąta 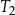 ma długość 50. Oblicz pole trójkąta
ma długość 50. Oblicz pole trójkąta 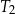 .
.
Wykaż, że jeżeli długości 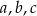 boków trójkąta spełniają równość
boków trójkąta spełniają równość
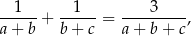
to promień okręgu opisanego na tym trójkącie jest równy 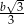 .
.
Dany jest trójkąt równoramienny 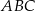 , w którym podstawa
, w którym podstawa 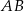 ma długość 12, a każde z ramion
ma długość 12, a każde z ramion 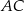 i
i 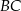 ma długość równą 10. Punkt
ma długość równą 10. Punkt 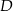 jest środkiem ramienia
jest środkiem ramienia 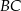 (zobacz rysunek).
(zobacz rysunek).
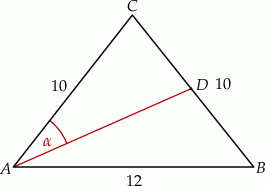
Oblicz sinus kąta  , jaki środkowa
, jaki środkowa 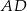 tworzy z ramieniem
tworzy z ramieniem 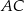 trójkąta
trójkąta 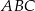 .
.
W trójkącie prostokątnym odległość punktu przecięcia się środkowych od wierzchołka kąta prostego wynosi 2 cm. Wysokość trójkąta poprowadzona na przeciwprostokątną ma długość 2,5 cm. Oblicz pole tego trójkąta.
