Odcinki 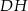 i
i 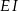 są równoległe do boku
są równoległe do boku 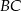 trójkąta
trójkąta 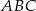 , a odcinki
, a odcinki 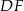 i
i 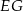 są równoległe do boku
są równoległe do boku 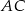 . Uzasadnij, że jeżeli
. Uzasadnij, że jeżeli 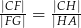 , to
, to 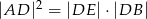 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Odcinki 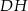 i
i 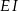 są równoległe do boku
są równoległe do boku 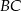 trójkąta
trójkąta 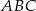 , a odcinki
, a odcinki 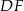 i
i 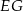 są równoległe do boku
są równoległe do boku 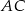 . Uzasadnij, że jeżeli
. Uzasadnij, że jeżeli 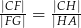 , to
, to 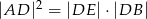 .
.

W trójkącie 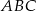 dane są
dane są 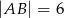 ,
, 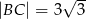 oraz
oraz 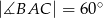 . Oblicz pole trójkąta
. Oblicz pole trójkąta 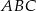 .
.
Punkt 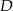 leży na boku
leży na boku 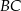 trójkąta równoramiennego
trójkąta równoramiennego 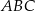 , w którym
, w którym 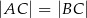 .
.
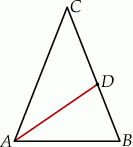
Odcinek 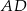 dzieli trójkąt
dzieli trójkąt 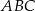 na dwa trójkąty równoramienne w taki sposób, że
na dwa trójkąty równoramienne w taki sposób, że 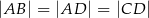 . Oblicz miary kątów trójkąta
. Oblicz miary kątów trójkąta 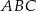 .
.
Dany jest trójkąt równoramienny 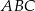 , w którym
, w którym 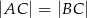 . Dwusieczna kąta
. Dwusieczna kąta 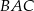 przecina bok
przecina bok 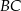 w takim punkcie
w takim punkcie 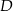 , że trójkąty
, że trójkąty 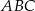 i
i 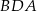 są podobne (zobacz rysunek). Oblicz miarę kąta
są podobne (zobacz rysunek). Oblicz miarę kąta 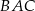 .
.
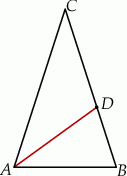
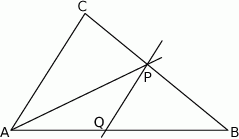
W trójkącie 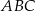 poprowadzono dwusieczne kątów przecinające boki
poprowadzono dwusieczne kątów przecinające boki 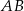 i
i 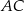 tego trójkąta w punktach – odpowiednio –
tego trójkąta w punktach – odpowiednio – 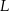 i
i 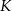 . Punkt
. Punkt 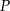 jest punktem przecięcia tych dwusiecznych. Długości boków trójkąta
jest punktem przecięcia tych dwusiecznych. Długości boków trójkąta 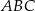 spełniają warunki:
spełniają warunki: 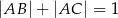 oraz
oraz
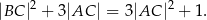
Udowodnij, że punkt 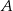 leży na okręgu opisanym na trójkącie
leży na okręgu opisanym na trójkącie 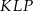 .
.
W trójkącie 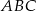 dwusieczna kąta
dwusieczna kąta 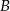 przecina bok
przecina bok 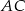 w punkcie
w punkcie 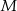 . Przez punkt
. Przez punkt 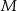 prowadzimy prostą równoległą do
prowadzimy prostą równoległą do 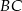 , przecinającą bok
, przecinającą bok 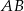 w punkcie
w punkcie 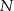 (rys.). Udowodnij, że
(rys.). Udowodnij, że 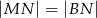 .
.
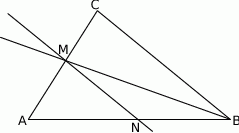
W trójkącie 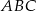 dwusieczna kąta
dwusieczna kąta 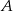 przecina bok
przecina bok 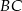 w punkcie
w punkcie 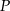 . Przez punkt
. Przez punkt 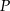 prowadzimy prostą równoległą do
prowadzimy prostą równoległą do 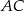 , przecinającą bok
, przecinającą bok 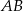 w punkcie
w punkcie 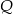 (rys.). Udowodnij, że
(rys.). Udowodnij, że 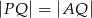 .
.
Dany jest trójkąt prostokątny 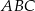 . Promień okręgu wpisanego w ten trójkąt jest pięć razy krótszy od przeciwprostokątnej tego trójkąta. Oblicz sinus tego z kątów ostrych trójkąta
. Promień okręgu wpisanego w ten trójkąt jest pięć razy krótszy od przeciwprostokątnej tego trójkąta. Oblicz sinus tego z kątów ostrych trójkąta 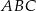 , który ma większą miarę.
, który ma większą miarę.
Dany jest trójkąt prostokątny 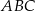 . Przeciwprostokątna tego trójkąta jest 6,5 razy dłuższa niż promień okręgu wpisanego w ten trójkąt. Oblicz sinus tego z kątów ostrych trójkąta
. Przeciwprostokątna tego trójkąta jest 6,5 razy dłuższa niż promień okręgu wpisanego w ten trójkąt. Oblicz sinus tego z kątów ostrych trójkąta 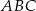 , który ma mniejszą miarę.
, który ma mniejszą miarę.
Wykaż, że jeżeli kąty 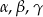 trójkąta
trójkąta 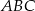 spełniają warunek
spełniają warunek 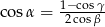 to trójkąt jest równoramienny.
to trójkąt jest równoramienny.
W trójkącie prostokątnym 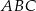 , w którym kąt przy wierzchołku
, w którym kąt przy wierzchołku 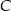 jest kątem prostym, poprowadzono środkowe
jest kątem prostym, poprowadzono środkowe 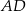 i
i 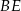 . Udowodnij, że
. Udowodnij, że 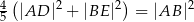 .
.
Liczby 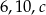 są długościami boków trójkąta prostokątnego. Oblicz
są długościami boków trójkąta prostokątnego. Oblicz  .
.
Podstawą trójkąta równoramiennego 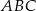 jest średnica
jest średnica 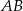 okręgu, którego środkiem jest punkt
okręgu, którego środkiem jest punkt 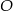 . Punkty
. Punkty 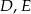 są punktami przecięcia ramion
są punktami przecięcia ramion 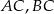 trójkąta z okręgiem. Miara kąta
trójkąta z okręgiem. Miara kąta 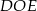 jest równa
jest równa 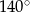 . Wykaż, że miara kąta
. Wykaż, że miara kąta 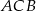 jest równa
jest równa 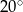 .
.
Punkty 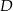 i
i 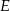 są takimi punktami przeciwprostokątnej
są takimi punktami przeciwprostokątnej 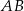 trójkąta prostokątnego
trójkąta prostokątnego 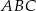 , że
, że 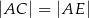 i
i 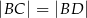 . Wykaż, że
. Wykaż, że 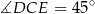 .
.
W trójkącie prostokątnym 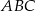 cosinus i tangens kąta przy wierzchołku
cosinus i tangens kąta przy wierzchołku 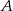 są równe. Oblicz sinus tego kąta.
są równe. Oblicz sinus tego kąta.
Punkt 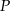 należy do boku
należy do boku 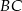 trójkąta równobocznego
trójkąta równobocznego 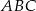 . Odcinek
. Odcinek 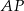 ma długość 6 i tworzy z bokiem
ma długość 6 i tworzy z bokiem 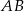 kąt
kąt 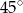 . Oblicz pole trójkąta
. Oblicz pole trójkąta 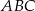 .
.
W trójkącie 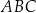 dane są długości boków
dane są długości boków 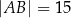 i
i 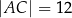 oraz
oraz 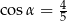 , gdzie
, gdzie 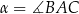 . Na bokach
. Na bokach 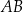 i
i 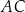 tego trójkąta obrano punkty odpowiednio
tego trójkąta obrano punkty odpowiednio 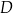 i
i 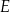 takie, że
takie, że 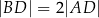 i
i 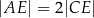 (zobacz rysunek).
(zobacz rysunek).

Oblicz pole
trójkąta 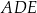 .
.
czworokąta 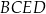 .
.
W trójkącie 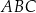 dane są długości boków
dane są długości boków 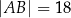 i
i 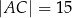 oraz
oraz 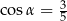 , gdzie
, gdzie 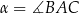 . Na bokach
. Na bokach 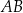 i
i 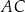 tego trójkąta obrano punkty odpowiednio
tego trójkąta obrano punkty odpowiednio 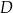 i
i 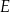 takie, że
takie, że 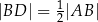 i
i 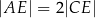 (zobacz rysunek).
(zobacz rysunek).

Oblicz pole
trójkąta 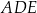 .
.
czworokąta 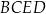 .
.
Z wierzchołków 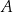 i
i 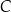 kątów ostrych równoramiennego trójkąta prostokątnego
kątów ostrych równoramiennego trójkąta prostokątnego 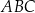 poprowadzono środkowe
poprowadzono środkowe 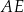 i
i 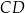 przecinające się w punkcie
przecinające się w punkcie 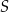 . Oblicz promień okręgu opisanego na trójkącie
. Oblicz promień okręgu opisanego na trójkącie 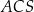 jeżeli
jeżeli 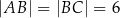 .
.
W trójkącie równoramiennym dany jest obwód 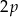 oraz miara kąta przy podstawie
oraz miara kąta przy podstawie  . Oblicz pole powierzchni tego trójkąta.
. Oblicz pole powierzchni tego trójkąta.
Liczby 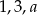 są długościami boków trójkąta. Wyznacz liczbę
są długościami boków trójkąta. Wyznacz liczbę  , wiedząc, że jest to liczba naturalna.
, wiedząc, że jest to liczba naturalna.
Na trójkącie o bokach długości 15, 20, 25 opisano okrąg. Oblicz długość środkowej tego trójkąta poprowadzonej do środka najdłuższego boku.
Boki trójkąta mają długości: 16, 10, 10. Wyznacz promień okręgu opisanego na tym trójkącie.
Dany jest trójkąt prostokątny 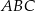 , w którym
, w którym 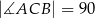 i
i 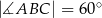 . Niech
. Niech 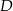 oznacza punkt wspólny wysokości poprowadzonej z wierzchołka
oznacza punkt wspólny wysokości poprowadzonej z wierzchołka 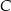 kąta prostego i przeciwprostokątnej
kąta prostego i przeciwprostokątnej 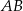 tego trójkąta. Wykaż, że
tego trójkąta. Wykaż, że 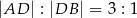 .
.
