W trójkącie równoramiennym 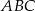 , gdzie
, gdzie 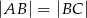 , podstawa ma długość 12. Punkt
, podstawa ma długość 12. Punkt 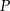 jest punktem przecięcia wysokości wychodzących z wierzchołków
jest punktem przecięcia wysokości wychodzących z wierzchołków 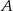 i
i 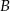 . Oblicz pole tego trójkąta, jeśli
. Oblicz pole tego trójkąta, jeśli 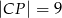 .
.
/Szkoła średnia/Geometria/Planimetria/Trójkąt
W trójkącie równoramiennym 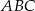 , gdzie
, gdzie 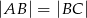 , podstawa ma długość 6. Punkt
, podstawa ma długość 6. Punkt 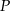 jest punktem przecięcia wysokości wychodzących z wierzchołków
jest punktem przecięcia wysokości wychodzących z wierzchołków 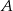 i
i 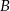 . Oblicz pole tego trójkąta, jeśli
. Oblicz pole tego trójkąta, jeśli 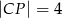 .
.
Na przeciwprostokątnej 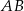 trójkąta prostokątnego
trójkąta prostokątnego 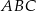 zbudowano kwadrat
zbudowano kwadrat 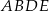 .
.
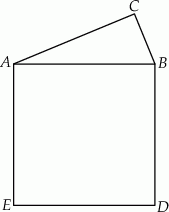
Stosunek pola trójkąta do pola kwadratu jest równy 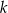 . Wykaż, że suma tangensów kątów ostrych tego trójkąta jest równa
. Wykaż, że suma tangensów kątów ostrych tego trójkąta jest równa 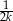 .
.
W trójkącie równobocznym 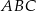 połączono środki wysokości otrzymując trójkąt
połączono środki wysokości otrzymując trójkąt 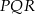 . Wykaż, że stosunek pola trójkąta
. Wykaż, że stosunek pola trójkąta 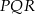 do pola trójkąta
do pola trójkąta 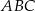 jest równy
jest równy 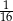 .
.
Odcinek 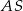 jest środkową trójkąta
jest środkową trójkąta 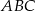 . Udowodnij, że
. Udowodnij, że 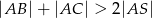 .
.
Okrąg wpisany w trójkąt 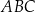 jest styczny do boków
jest styczny do boków 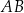 i
i 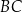 w punktach
w punktach 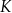 i
i 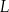 odpowiednio. Na bokach
odpowiednio. Na bokach 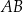 i
i 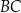 tego trójkąta wybrano punkty
tego trójkąta wybrano punkty 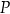 i
i 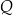 w ten sposób, że odcinek
w ten sposób, że odcinek 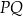 jest styczny do okręgu wpisanego w trójkąt
jest styczny do okręgu wpisanego w trójkąt 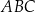 (zobacz rysunek).
(zobacz rysunek).

Wykaż, że jeżeli 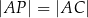 ,
, 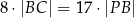 i
i 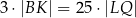 , to trójkąt
, to trójkąt 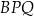 jest rozwartokątny.
jest rozwartokątny.
Sprawdź, czy trójkąt o bokach: 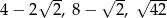 jest trójkątem prostokątnym.
jest trójkątem prostokątnym.
Sprawdź, czy trójkąt o bokach: 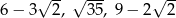 jest trójkątem prostokątnym.
jest trójkątem prostokątnym.
Ile jest trójkątów o obwodzie równym 19, w których długości boków wyrażone są liczbami całkowitymi. Wymień je.
Punkty 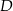 i
i 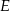 dzielą bok
dzielą bok 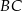 trójkąta
trójkąta 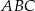 na trzy równe części (zobacz rysunek). Wykaż, że pole trójkąta
na trzy równe części (zobacz rysunek). Wykaż, że pole trójkąta 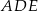 jest trzy razy mniejsze od pola trójkąta
jest trzy razy mniejsze od pola trójkąta 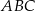 .
.
W trójkącie  dane są:
dane są: 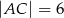 ,
, 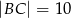 i kąt
i kąt 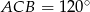 . Wyznacz długość środkowej
. Wyznacz długość środkowej 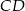 tego trójkąta.
tego trójkąta.
Wykaż, że suma odległości dowolnego punktu wewnętrznego trójkąta od jego wierzchołków jest większa od połowy obwodu trójkąta.
W rozwartokątnym trójkącie równoramiennym 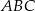 (
(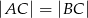 ) odległość środka koła wpisanego w trójkąt od wierzchołka
) odległość środka koła wpisanego w trójkąt od wierzchołka 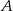 jest równa
jest równa 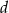 , a
, a 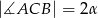 . Oblicz pole trójkąta
. Oblicz pole trójkąta 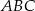 i promień koła opisanego na trójkącie
i promień koła opisanego na trójkącie 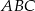 .
.
W ostrokątnym trójkącie równoramiennym ramię ma długość 61, a wysokość poprowadzona do ramienia ma długość 11. Oblicz długość podstawy tego trójkąta.
Na rysunku przedstawiono trójkąt 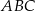 , w którym
, w którym 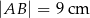 oraz odcinek
oraz odcinek 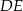 równoległy do boku
równoległy do boku 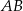 trójkąta.
trójkąta.
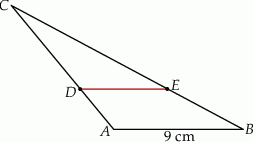
Stosunek pola trapezu 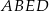 do pola trójkąta
do pola trójkąta 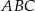 jest równy
jest równy 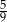 . Oblicz długość odcinka
. Oblicz długość odcinka 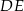 .
.
Oblicz wysokość trójkąta prostokątnego o przyprostokątnych 12 cm i 9 cm, która jest poprowadzona do przeciwprostokątnej.
Trójkąt prostokątny ma przyprostokątne długości 6 i 8. Wyznacz długość najkrótszej wysokości tego trójkąta.
Trójkąt prostokątny ma przyprostokątne długości 12 i 5. Wyznacz długość najkrótszej wysokości tego trójkąta.
Na rysunku oznaczono kąty oraz podano długości boków trójkąta prostokątnego. Oblicz, które z wyrażeń ma większą wartość: 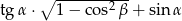 czy
czy 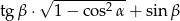 .
.
W trójkącie prostokątnym  wysokość
wysokość  dzieli przeciwprostokątną
dzieli przeciwprostokątną 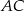 na odcinki o długościach
na odcinki o długościach 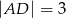 i
i 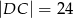 .
.
- Oblicz długości boków trójkąta
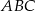 .
. - Oblicz długość odcinka
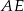 , gdzie
, gdzie 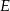 jest punktem wspólnym dwusiecznej kąta
jest punktem wspólnym dwusiecznej kąta 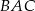 i boku
i boku 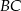 .
.
Wysokość 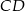 trójkąta
trójkąta 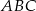 ma długość 6cm i dzieli bok
ma długość 6cm i dzieli bok 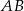 na odcinki o długościach
na odcinki o długościach 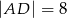 i
i 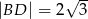 .
.
- Oblicz tangens i cosinus kąta
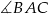 .
. - Znajdź miarę kąta
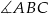 .
.
Dany jest trójkąt prostokątny o przyprostokątnych długości: 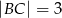 i
i 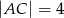 . Na boku
. Na boku 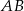 tego trójkąta wybrano taki punkt
tego trójkąta wybrano taki punkt  , że
, że 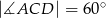 . Oblicz długość odcinka
. Oblicz długość odcinka 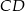 .
.
W trójkącie prostokątnym 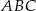 przyprostokątne mają długości
przyprostokątne mają długości 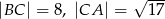 . Na boku
. Na boku 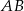 wybrano punkt
wybrano punkt  tak, że
tak, że 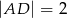 . Oblicz sinus kąta
. Oblicz sinus kąta  .
.
Wykaż, że odcinek łączący środki dwóch boków trójkąta jest równoległy do trzeciego boku i ma długość równą połowie tego boku.

