Dwusieczne kątów 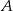 i
i 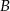 trójkąta
trójkąta 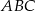 przecinają okrąg opisany na nim odpowiednio w punktach
przecinają okrąg opisany na nim odpowiednio w punktach 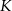 i
i 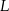 . Oblicz miary kątów czworokąta
. Oblicz miary kątów czworokąta 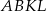 wiedząc, że
wiedząc, że 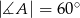 i
i 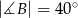 .
.
/Szkoła średnia/Geometria/Planimetria/Trójkąt
W trójkącie ostrokątnym 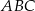 prawdziwa jest równość
prawdziwa jest równość 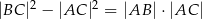 . Wykaż, że kąt
. Wykaż, że kąt 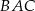 jest dwa razy większy od kąta
jest dwa razy większy od kąta 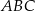 .
.
W trójkąt równoramienny wpisano kwadrat w ten sposób, że dwa jego wierzchołki leżą na podstawie trójkąta, a dwa pozostałe są środkami ramion. Jaką część pola trójkąta stanowi pole kwadratu? Odpowiedź uzasadnij.
Wykaż, że jeżeli w trójkącie dwusieczna pokrywa się ze środkową, to trójkąt ten jest równoramienny.
Wyraź pole trójkąta w zależności od długości jednego z jego boków i miar kątów doń przyległych.
W trójkącie 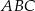 punkt
punkt 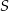 jest środkiem okręgu wpisanego, a punkty
jest środkiem okręgu wpisanego, a punkty 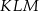 są punktami styczności okręgu wpisanego w trójkąt z bokami
są punktami styczności okręgu wpisanego w trójkąt z bokami 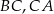 i
i 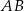 odpowiednio.
odpowiednio.
- Uzasadnij, że na czworokącie
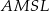 można opisać okrąg.
można opisać okrąg. - Wiedząc, że
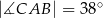 oraz
oraz 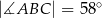 oblicz miary kątów trójkąta
oblicz miary kątów trójkąta 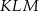 .
.
Wykaż, że jeżeli 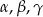 są kątami trójkąta, to
są kątami trójkąta, to
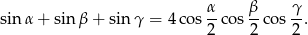
Punkty 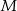 i
i 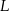 leżą odpowiednio na bokach
leżą odpowiednio na bokach 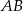 i
i 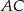 trójkąta
trójkąta 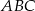 , przy czym zachodzą równości
, przy czym zachodzą równości 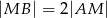 oraz
oraz 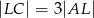 . Punkt
. Punkt 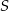 jest punktem przecięcia odcinków
jest punktem przecięcia odcinków 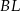 i
i 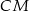 . Punkt
. Punkt 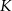 jest punktem przecięcia półprostej
jest punktem przecięcia półprostej 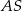 z odcinkiem
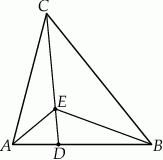
z odcinkiem 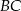 (zobacz rysunek).
(zobacz rysunek).
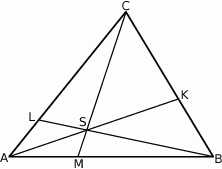
Pole trójkąta 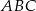 jest równe 660. Oblicz pola trójkątów:
jest równe 660. Oblicz pola trójkątów: 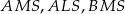 i
i 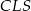 .
.
Punkty 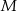 i
i 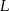 leżą odpowiednio na bokach
leżą odpowiednio na bokach 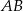 i
i 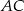 trójkąta
trójkąta 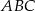 , przy czym zachodzą równości
, przy czym zachodzą równości 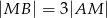 oraz
oraz 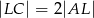 . Punkt
. Punkt 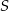 jest punktem przecięcia odcinków
jest punktem przecięcia odcinków 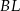 i
i 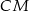 . Punkt
. Punkt 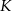 jest punktem przecięcia półprostej
jest punktem przecięcia półprostej 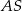 z odcinkiem
z odcinkiem 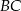 (zobacz rysunek).
(zobacz rysunek).
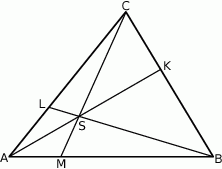
Pole trójkąta 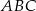 jest równe 528. Oblicz pola trójkątów:
jest równe 528. Oblicz pola trójkątów: 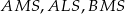 i
i 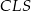 .
.
W trójkącie 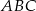 środkowa
środkowa 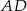 jest prostopadła do boku
jest prostopadła do boku 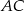 . Kąt
. Kąt 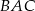 ma miarę
ma miarę 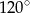 . Wykaż, że
. Wykaż, że 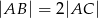 .
.
Na boku 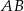 trójkąta
trójkąta 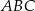 wybrano punkt
wybrano punkt 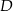 , a na odcinku
, a na odcinku 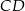 wybrano punkt
wybrano punkt 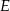 . Wykaż, że stosunek pól trójkątów
. Wykaż, że stosunek pól trójkątów 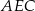 i
i 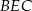 jest równy stosunkowi pól trójkątów
jest równy stosunkowi pól trójkątów 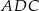 i
i 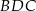 .
.
Przez środek 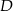 przyprostokątnej
przyprostokątnej 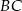 trójkąta prostokątnego
trójkąta prostokątnego 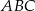 poprowadzono prostą prostopadłą do przeciwprostokątnej
poprowadzono prostą prostopadłą do przeciwprostokątnej 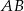 . Prosta ta przecina proste
. Prosta ta przecina proste 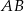 i
i 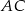 odpowiednio w punktach
odpowiednio w punktach 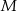 i
i 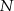 . Wykaż, że
. Wykaż, że 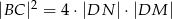 .
.
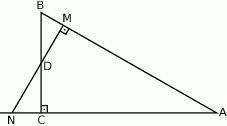
Przez środek 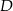 przyprostokątnej
przyprostokątnej 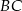 trójkąta prostokątnego
trójkąta prostokątnego 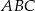 poprowadzono prostą prostopadłą do przeciwprostokątnej
poprowadzono prostą prostopadłą do przeciwprostokątnej 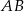 . Prosta ta przecina proste
. Prosta ta przecina proste 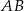 i
i 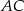 odpowiednio w punktach
odpowiednio w punktach 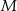 i
i 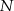 . Wykaż, że skala podobieństwa trójkątów
. Wykaż, że skala podobieństwa trójkątów 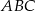 i
i 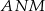 jest równa
jest równa 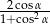 .
.
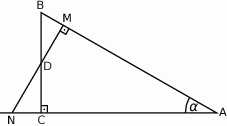
Środkowa 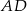 trójkąta
trójkąta 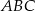 ma długość równą połowie długości boku
ma długość równą połowie długości boku 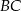 oraz
oraz 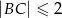 . Wykaż, że
. Wykaż, że 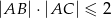 .
.
Dany jest trójkąt rozwartokątny 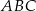 , w którym
, w którym 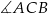 ma miarę
ma miarę 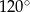 . Ponadto wiadomo, że
. Ponadto wiadomo, że 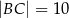 i
i 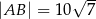 (zobacz rysunek). Oblicz długość trzeciego boku trójkąta
(zobacz rysunek). Oblicz długość trzeciego boku trójkąta 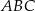 .
.
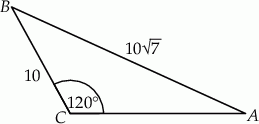
Dany jest trójkąt 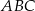 , w którym
, w którym 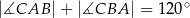 . Ponadto wiadomo, że
. Ponadto wiadomo, że 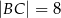 i
i 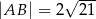 (zobacz rysunek). Oblicz długość trzeciego boku trójkąta
(zobacz rysunek). Oblicz długość trzeciego boku trójkąta 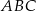 .
.
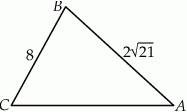
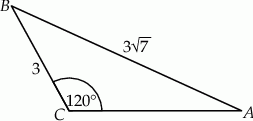
Dany jest trójkąt rozwartokątny 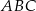 , w którym
, w którym 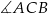 ma miarę
ma miarę 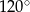 . Ponadto wiadomo, że
. Ponadto wiadomo, że 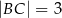 i
i 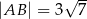 (zobacz rysunek). Oblicz długość trzeciego boku trójkąta
(zobacz rysunek). Oblicz długość trzeciego boku trójkąta 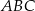 .
.
Podstawa 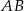 trójkąta równoramiennego
trójkąta równoramiennego 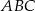 ma długość 4, a ramiona mają długość 8.
ma długość 4, a ramiona mają długość 8.
- Oblicz długość promienia okręgu wpisanego w ten trójkąt.
- Oblicz dlugość promienia okręgu opisanego na tym trójkącie.
W trójkącie 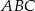 dane są długości boków
dane są długości boków 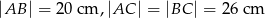 . Wyznacz długość środkowej
. Wyznacz długość środkowej 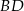 .
.
Wiedząc, że boki trójkąta prostokątnego mają długości: 20, 15, 25, wyznacz długość wysokości opuszczonej na przeciwprostokątną.
Boki trójkąta prostokątnego mają długości 10,24,26. Oblicz długość wysokości opuszczonej na przeciwprostokątną.
Na przyprostokątnych 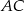 i
i 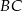 trójkąta prostokątnego
trójkąta prostokątnego 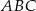 zbudowano trójkąty równoramienne
zbudowano trójkąty równoramienne 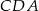 i
i 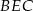 w ten sposób, że
w ten sposób, że 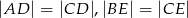 oraz punkty
oraz punkty 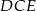 leżą na jednej prostej. Wykaż, że proste
leżą na jednej prostej. Wykaż, że proste 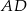 i
i 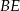 są równoległe.
są równoległe.
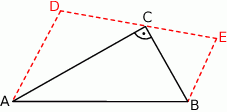
Kąty ostre trójkąta 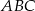 o polu
o polu 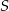 mają miary
mają miary 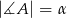 ,
, 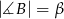 . Oblicz długości boków
. Oblicz długości boków 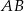 i
i 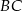 tego trójkąta.
tego trójkąta.
Promień okręgu wpisanego w trójkąt o bokach 5 i 8 jest równy równy 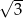 , a obwód tego trójkąta jest liczbą całkowitą. Oblicz długość trzeciego boku tego trójkąta.
, a obwód tego trójkąta jest liczbą całkowitą. Oblicz długość trzeciego boku tego trójkąta.
Dwa trójkąty równoboczne mają wspólny środek i boki równoległe. Pole jednego jest 2 razy większe od pola drugiego, a boki mniejszego trójkąta mają długość 1. Jaka jest odległość między równoległymi bokami?

