W trójkącie 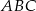 kąt przy wierzchołku
kąt przy wierzchołku 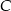 jest prosty. Trójkąt
jest prosty. Trójkąt 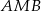 jest równoboczny. Oblicz miary kątów ostrych trójkąta
jest równoboczny. Oblicz miary kątów ostrych trójkąta 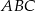 , jeśli pole trójkąta
, jeśli pole trójkąta 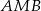 jest dwa razy większe od pola trójkąta
jest dwa razy większe od pola trójkąta 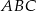 .
.
/Szkoła średnia/Geometria/Planimetria/Trójkąt
W trójkącie prostokątnym 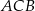 przyprostokątna
przyprostokątna 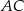 ma długość 5, a promień okręgu wpisanego w ten trójkąt jest równy 2. Oblicz pole trójkąta
ma długość 5, a promień okręgu wpisanego w ten trójkąt jest równy 2. Oblicz pole trójkąta 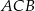 .
.
W trójkącie prostokątnym 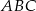 dane są
dane są 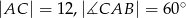 . Poprowadzono prostą równoległą do przeciwprostokątnej
. Poprowadzono prostą równoległą do przeciwprostokątnej 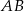 dzielącą bok
dzielącą bok 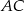 w stosunku
w stosunku 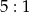 , licząc od wierzchołka
, licząc od wierzchołka 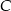 . Prosta ta przecina bok
. Prosta ta przecina bok 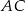 w punkcie
w punkcie 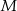 , a bok
, a bok 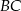 w punkcie
w punkcie 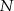 . Oblicz pole trapezu
. Oblicz pole trapezu 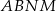 .
.
Uzasadnij, że przeciwprostokątna trójkąta prostokątnego jest średnicą okręgu na nim opisanego.
Udowodnij, że w trójkącie równoramiennym wysokości poprowadzone do równych boków są równej długości.
Oblicz tangens kąta ostrego utworzonego przez proste zawierające środkowe trójkąta prostokątnego równoramiennego poprowadzone na przyprostokątne.
W trójkącie 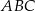 kąt przy wierzchołku
kąt przy wierzchołku 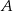 jest prosty, a kąt przy wierzchołku
jest prosty, a kąt przy wierzchołku 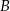 ma miarę
ma miarę 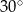 . Na boku
. Na boku 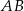 tego trójkąta obrano punkt
tego trójkąta obrano punkt 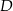 tak, że miara kąta
tak, że miara kąta 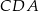 jest równa
jest równa 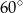 oraz
oraz 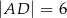 (zobacz rysunek). Oblicz
(zobacz rysunek). Oblicz 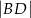 .
.
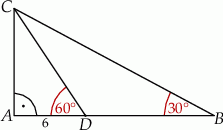
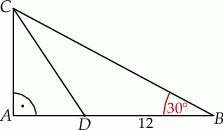
W trójkącie 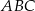 kąt przy wierzchołku
kąt przy wierzchołku 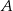 jest prosty, a kąt przy wierzchołku
jest prosty, a kąt przy wierzchołku 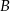 ma miarę
ma miarę 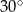 . Na boku
. Na boku 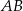 tego trójkąta obrano punkt
tego trójkąta obrano punkt 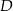 tak, że odcinek
tak, że odcinek 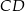 jest dwusieczną kąta przy wierzchołku
jest dwusieczną kąta przy wierzchołku 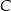 oraz
oraz 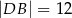 (zobacz rysunek). Oblicz
(zobacz rysunek). Oblicz 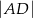 .
.
Punkt 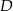 jest środkiem boku
jest środkiem boku 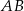 trójkąta
trójkąta 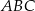 oraz
oraz 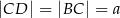 ,
, 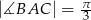 . Oblicz długości boków
. Oblicz długości boków 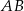 i
i 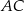 trójkąta
trójkąta 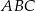 .
.
Na bokach 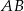 ,
, 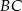 i
i 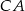 trójkąta
trójkąta 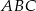 wybrano odpowiednio punkty
wybrano odpowiednio punkty 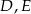 i
i 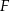 . Wykaż, że okręgi opisane na trójkątach
. Wykaż, że okręgi opisane na trójkątach 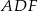 ,
, 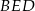 i
i 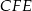 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.
Przyprostokątna trójkąta prostokątnego ma długość 10. Miara kąta ostrego leżącego naprzeciw tej przyprostokątnej wynosi 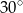 . Oblicz długość okręgu opisanego na tym trójkącie.
. Oblicz długość okręgu opisanego na tym trójkącie.
Przyprostokątna trójkąta prostokątnego ma długość 12. Miara kąta ostrego leżącego przy tej przyprostokątnej wynosi 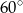 . Oblicz długość okręgu opisanego na tym trójkącie.
. Oblicz długość okręgu opisanego na tym trójkącie.
Na przedłużeniu przeciwprostokątnej 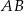 trójkąta prostokątnego
trójkąta prostokątnego 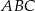 wybrano punkt
wybrano punkt 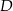 tak, że
tak, że 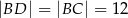 . Oblicz długość odcinka
. Oblicz długość odcinka 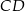 jeżeli
jeżeli 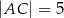 .
.
W trójkąt równoramienny 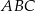 o podstawie długości
o podstawie długości 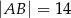 i polu 168 wpisano okrąg. Oblicz długość odcinka łączącego wierzchołek
i polu 168 wpisano okrąg. Oblicz długość odcinka łączącego wierzchołek 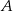 z punktem wspólnym okręgu i ramienia
z punktem wspólnym okręgu i ramienia 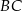 .
.
W trójkącie 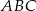 środkowe
środkowe 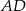 i
i 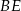 są prostopadłe. Wykaż, że
są prostopadłe. Wykaż, że 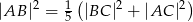 .
.
W trójkącie 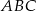 dwa kąty przy wierzchołkach
dwa kąty przy wierzchołkach 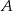 i
i 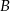 mają odpowiednio miary:
mają odpowiednio miary: 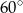 i
i 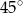 . Oblicz pole tego trójkąta, wiedząc, że długość boku
. Oblicz pole tego trójkąta, wiedząc, że długość boku 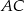 jest równa
jest równa 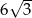 .
.
Wykaż, że jeśli 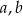 są długościami boków trójkąta ostrokątnego takimi, że
są długościami boków trójkąta ostrokątnego takimi, że 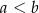 oraz
oraz 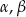 są miarami kątów tego trójkąta leżącymi odpowiednio naprzeciwko boków
są miarami kątów tego trójkąta leżącymi odpowiednio naprzeciwko boków 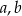 , to
, to 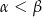 .
.
W okrąg o promieniu 13 wpisano rozwartokątny trójkąt równoramienny o podstawie 10. Oblicz pole tego trójkąta.
Dany jest trójkąt 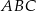 , w którym
, w którym 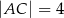 ,
, 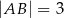 ,
, 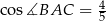 . Oblicz pole trójkąta
. Oblicz pole trójkąta 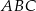 .
.
Dany jest trójkąt 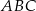 , w którym
, w którym 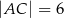 ,
, 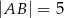 ,
, 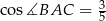 . Oblicz pole trójkąta
. Oblicz pole trójkąta 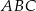 .
.
Dany jest trójkąt 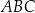 . Na boku
. Na boku 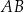 tego trójkąta wybrano punkt
tego trójkąta wybrano punkt 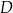 , taki, że
, taki, że 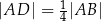 , a na boku
, a na boku 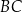 wybrano taki punkt
wybrano taki punkt 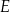 , że
, że 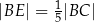 (zobacz rysunek poniżej). Pole trójkąta
(zobacz rysunek poniżej). Pole trójkąta 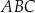 jest równe 20.
jest równe 20.

Oblicz pole trójkąta 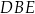 .
.
W trójkącie 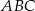 punkt
punkt 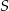 jest środkiem okręgu wpisanego, a punkty
jest środkiem okręgu wpisanego, a punkty 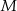 i
i 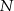 są punktami styczności tego okręgu z bokami
są punktami styczności tego okręgu z bokami 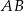 i
i 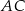 odpowiednio. Wykaż, że punkt
odpowiednio. Wykaż, że punkt 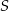 leży na okręgu opisanym na trójkącie
leży na okręgu opisanym na trójkącie 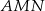 .
.
Dany jest trójkąt równoramienny 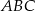 , w którym
, w którym 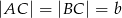 i
i 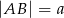 . Punkty
. Punkty 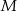 i
i 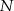 są rzutami prostopadłymi środka podstawy
są rzutami prostopadłymi środka podstawy 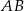 trójkąta na ramiona
trójkąta na ramiona 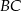 i
i 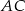 . Wyraź pole czworokąta
. Wyraź pole czworokąta 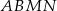 za pomocą
za pomocą  i
i 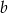 .
.

