Dany jest trójkąt równoramienny  , w którym
, w którym  i
i  . Punkty
. Punkty 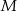 i
i 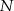 są rzutami prostopadłymi środka podstawy
są rzutami prostopadłymi środka podstawy 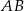 trójkąta na ramiona
trójkąta na ramiona 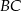 i
i 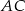 . Wyraź pole czworokąta
. Wyraź pole czworokąta 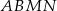 za pomocą
za pomocą  i
i 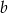 .
.
/Szkoła średnia/Geometria/Planimetria/Trójkąt
Dany jest trójkąt równoramienny 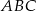 , w którym
, w którym 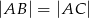 i
i 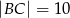 . Na boku
. Na boku 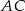 wybrano punkt
wybrano punkt 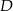 w ten sposób, że
w ten sposób, że 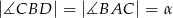 oraz
oraz 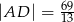 . Oblicz
. Oblicz 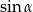 .
.
Stosunek pól dwóch trójkątów podobnych jest równy 4, a suma ich obwodów 12. Wyznacz obwód każdego z tych trójkątów.
Stosunek pól dwóch trójkątów podobnych jest równy 4, a suma ich obwodów 18. Wyznacz obwód każdego z tych trójkątów.
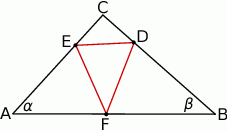
Dany jest trójkąt 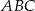 , w którym
, w którym 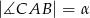 i
i 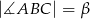 (zobacz rysunek). Na bokach
(zobacz rysunek). Na bokach 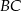 ,
, 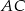 i
i 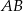 tego trójkąta wybrano odpowiednio punkty
tego trójkąta wybrano odpowiednio punkty 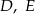 i
i 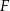 w taki sposób, że
w taki sposób, że 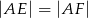 ,
, 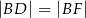 i
i 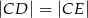 . Oblicz miary kątów trójkąta
. Oblicz miary kątów trójkąta 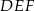 .
.
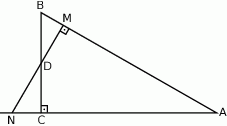
W trójkącie prostokątnym 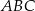 punkt
punkt 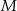 leży na przeciwprostokątnej
leży na przeciwprostokątnej 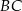 . Z punktu
. Z punktu 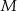 poprowadzono odcinki
poprowadzono odcinki 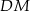 i
i 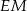 prostopadłe odpowiednio do przyprostokątnych
prostopadłe odpowiednio do przyprostokątnych 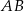 i
i 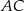 (rysunek).
(rysunek).
Udowodnij, że
Trójkąt  jest prostokątny. Z punktu
jest prostokątny. Z punktu 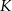 należącego do przeciwprostokątnej
należącego do przeciwprostokątnej 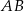 poprowadzono odcinki
poprowadzono odcinki 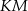 oraz
oraz 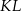 prostopadłe odpowiednio do przyprostokątnych
prostopadłe odpowiednio do przyprostokątnych 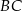 oraz
oraz  (rysunek).
(rysunek).
Wykaż, że
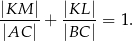
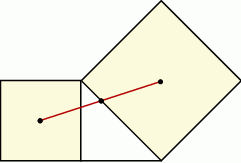
Na zewnątrz równoramiennego trójkąta prostokątnego zbudowano kwadraty – jeden na przyprostokątnej, a drugi na przeciwprostokątnej. Wykaż, że przeciwprostokątna dzieli odcinek łączący środki kwadratów na dwie równe części.
Wysokość trójkąta 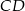 ma długość 4 i dzieli bok
ma długość 4 i dzieli bok 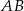 na odcinki, z których krótszy
na odcinki, z których krótszy 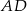 ma długość 2, a kąt
ma długość 2, a kąt 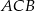 na kąty, których stosunek miar jest równy 1:2. Oblicz długość boku
na kąty, których stosunek miar jest równy 1:2. Oblicz długość boku 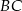 tego trójkąta.
tego trójkąta.
Wykaż, że jeżeli 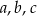 są długościami boków trójkąta leżącymi naprzeciwko odpowiednio kątów o miarach
są długościami boków trójkąta leżącymi naprzeciwko odpowiednio kątów o miarach 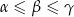 to
to 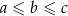 .
.
Trójkąt prostokątny ma boki długości 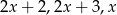 . Wyznacz
. Wyznacz  oraz promień okręgu wpisanego w ten trójkąt.
oraz promień okręgu wpisanego w ten trójkąt.
Dane są dwa boki trójkąta: 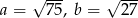 . Jaką długość może przyjmować trzeci bok trójkąta?
. Jaką długość może przyjmować trzeci bok trójkąta?
Każdy kąt trójkąta 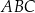 ma miarę mniejszą niż
ma miarę mniejszą niż 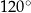 . Udowodnij, że wewnątrz trójkąta
. Udowodnij, że wewnątrz trójkąta 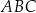 istnieje punkt
istnieje punkt 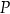 taki, że
taki, że
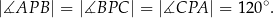
Pole trójkąta ostrokątnego o bokach 40 i 29 jest równe 420. Oblicz długość promienia okręgu wpisanego w ten trójkąt.
W trójkącie 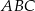 środkowa
środkowa 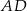 jest prostopadła do boku
jest prostopadła do boku 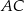 . Kąt
. Kąt 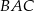 ma miarę
ma miarę 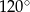 oraz
oraz 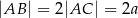 . Oblicz długość odcinka
. Oblicz długość odcinka 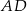 .
.
Dwa boki trójkąta ostrokątnego wpisanego w okrąg o promieniu 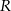 mają długości
mają długości 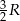 i
i 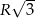 . Wykaż, że długość trzeciego boku wynosi
. Wykaż, że długość trzeciego boku wynosi 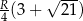 .
.
Trzy cięciwy okręgu o promieniu  tworzą trójkąt wpisany w ten okrąg. Dwie najkrótsze z tych cięciw mają długości
tworzą trójkąt wpisany w ten okrąg. Dwie najkrótsze z tych cięciw mają długości 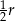 i
i 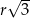 . Wykaż, że trzecia cięciwa ma długość
. Wykaż, że trzecia cięciwa ma długość 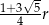 .
.
Pole trójkąta równoramiennego jest równe 25. Oblicz długość promienia okręgu wpisanego w trójkąt wiedząc, że ramię jest dwa razy dłuższe od podstawy.
Wykaż, że jeżeli 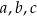 są długościami boków trójkąta to
są długościami boków trójkąta to 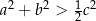 .
.
Na bokach trójkąta zbudowano kwadraty o polach 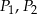 i
i 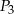 (zobacz rysunek)
(zobacz rysunek)
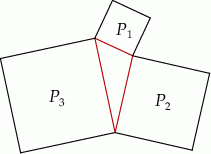
Wykaż, że 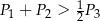 .
.
Wyznacz długość przeciwprostokątnej oraz miary kątów trójkąta prostokątnego, którego przyprostokątne mają długości 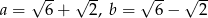 .
.
Trójkąt podzielono odcinkami 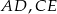 i
i 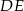 na 5 trójkątów, przy czym
na 5 trójkątów, przy czym 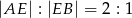 .
.
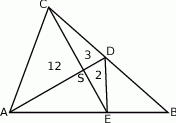
Korzystając z podanych pól trzech z tych trójkątów, wyznacz pole trójkąta 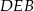 .
.
Podstawa trójkąta równoramiennego ma długość 4. Środek okręgu opisanego na tym trójkącie dzieli jedną z wysokości trójkąta na odcinki, których stosunek długości wynosi 3:5. Oblicz długość ramienia trójkąta.
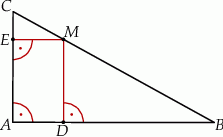
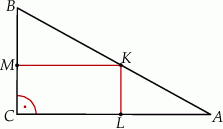
Przez środek 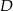 przyprostokątnej
przyprostokątnej 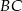 trójkąta prostokątnego
trójkąta prostokątnego 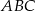 poprowadzono prostą prostopadłą do przeciwprostokątnej
poprowadzono prostą prostopadłą do przeciwprostokątnej 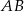 . Prosta ta przecina proste
. Prosta ta przecina proste 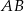 i
i 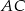 odpowiednio w punktach
odpowiednio w punktach 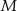 i
i 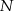 . Wykaż, że
. Wykaż, że 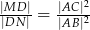 .
.