Ramię trójkąta równoramiennego jest dwa razy dłuższe od podstawy. Wyznacz obwód trójkąta, jeśli środkowa poprowadzona do ramienia ma długość 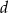 .
.
/Szkoła średnia/Geometria/Planimetria/Trójkąt
Podstawa trójkąta równoramiennego ma długość 10, a cosinus jednego z jego kątów jest równy 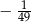 . Oblicz pole tego trójkąta.
. Oblicz pole tego trójkąta.
W trójkącie równoramiennym ramię jest 2 razy dłuższe od podstawy. Suma długości promieni okręgu wpisanego i opisanego na tym trójkącie równa się 11. Oblicz długość podstawy trójkąta.
Długości dwóch boków trójkąta są równe 1 i 4, a miara kąta zawartego między nimi wynosi 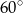 .
.
- Oblicz pole tego trójkąta.
- Oblicz promień okręgu opisanego na tym trójkącie.
- Oblicz promień okręgu wpisanego w ten trójkąt.
Wykaż, że jeżeli pole trójkąta prostokątnego jest równe 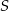 , to długość jego przeciwprostokątnej jest nie mniejsza niż
, to długość jego przeciwprostokątnej jest nie mniejsza niż 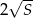 .
.
Dwusieczna kąta ostrego 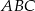 przecina przyprostokątną
przecina przyprostokątną 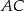 trójkąta prostokątnego
trójkąta prostokątnego 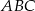 w punkcie
w punkcie 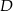 .
.
Udowodnij, że jeżeli 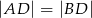 , to
, to 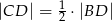 .
.
Dwusieczna kąta ostrego 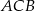 przecina przyprostokątną
przecina przyprostokątną 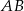 trójkąta prostokątnego
trójkąta prostokątnego 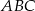 w punkcie
w punkcie 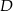 .
.
Udowodnij, że jeżeli 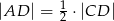 , to
, to 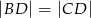 .
.
Styczna w punkcie  do okręgu opisanego na trójkącie
do okręgu opisanego na trójkącie 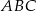 przecina prostą
przecina prostą 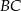 w punkcie
w punkcie 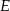 . Niech
. Niech 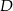 będzie punktem przecięcia dwusiecznej kąta
będzie punktem przecięcia dwusiecznej kąta 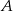 z prostą
z prostą 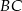 . Udowodnić, że
. Udowodnić, że 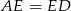 .
.
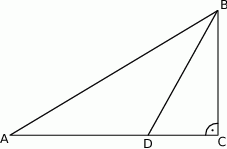
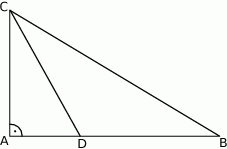
Dany jest trójkąt równoramienny 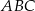 , w którym podstawa
, w którym podstawa 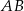 ma długość 32, a każde z ramion
ma długość 32, a każde z ramion 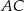 i
i 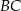 ma długość równą 34. Punkt
ma długość równą 34. Punkt 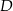 jest środkiem ramienia
jest środkiem ramienia  (zobacz rysunek).
(zobacz rysunek).
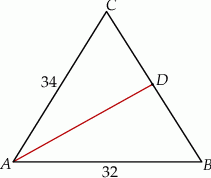
Oblicz długość odcinka 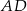 .
.
Oblicz długości boków trójkąta prostokątnego  (
(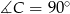 ) jeżeli
) jeżeli 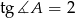 i
i 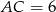 .
.
W trójkąt równoboczny wpisane są 3 koła o równych promieniach, przy czym każde koło jest styczne do dwóch boków trójkąta oraz do dwóch pozostałych kół. Oblicz stosunek sumy pól tych kół do pola trójkąta.
W trójkącie 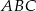 , o bokach długości
, o bokach długości 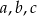 , połączono odcinkiem wierzchołek
, połączono odcinkiem wierzchołek 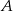 z punktem
z punktem 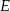 na boku
na boku 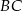 takim, że
takim, że 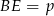 i
i 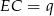 . Uzasadnij, że jeżeli
. Uzasadnij, że jeżeli 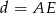 , to
, to 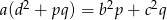 (twierdzenie Stewarta).
(twierdzenie Stewarta).
W okrąg wpisano trójkąt 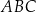 , w którym
, w którym 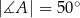 i
i 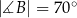 . Przez wierzchołek kąta
. Przez wierzchołek kąta 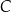 poprowadzono styczną do okręgu, przecinającą przedłużenie boku
poprowadzono styczną do okręgu, przecinającą przedłużenie boku 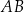 w punkcie
w punkcie 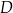 . Oblicz miary kątów trójkąta
. Oblicz miary kątów trójkąta 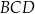 .
.
Wyznacz długości boków trójkąta prostokątnego, w którym długość przyprostokątnej wynosi 12 cm, a kąt do niej przyległy ma miarę 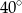 . Wynik podaj z dokładnością do 0,1 cm.
. Wynik podaj z dokładnością do 0,1 cm.
W trójkącie 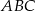 wysokość
wysokość 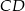 dzieli bok
dzieli bok 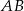 na odcinki długości
na odcinki długości 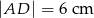 i
i 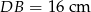 . Bok
. Bok 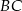 ma 20 cm długości. Poprowadzono symetralną boku
ma 20 cm długości. Poprowadzono symetralną boku 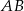 . Wyznacz długości odcinków, na jakie symetralna ta podzieliła bok
. Wyznacz długości odcinków, na jakie symetralna ta podzieliła bok 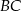 .
.
W trójkącie 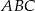 wysokość
wysokość 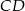 dzieli bok
dzieli bok 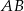 na odcinki długości
na odcinki długości 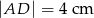 i
i 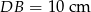 . Bok
. Bok 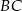 ma 16 cm długości. Poprowadzono symetralną boku
ma 16 cm długości. Poprowadzono symetralną boku 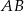 . Wyznacz długości odcinków, na jakie symetralna ta podzieliła bok
. Wyznacz długości odcinków, na jakie symetralna ta podzieliła bok 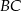 .
.
Oblicz długość promienia okręgu wpisanego w trójkąt prostokątny, którego kąt ostry ma miarę 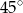 , a długość przeciwprostokątnej jest równa 4.
, a długość przeciwprostokątnej jest równa 4.
W trójkącie 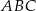 boki
boki 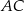 i
i 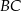 są równe. Okrąg, którego średnicą jest wysokość
są równe. Okrąg, którego średnicą jest wysokość 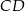 trójkąta przecina boki trójkąta w punktach dzielących te boki w stosunku 5:3 licząc od wierzchołka
trójkąta przecina boki trójkąta w punktach dzielących te boki w stosunku 5:3 licząc od wierzchołka 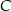 . Oblicz pole trójkąta
. Oblicz pole trójkąta 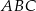 , jeżeli
, jeżeli 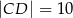 .
.
Podstawa trójkąta równoramiennego ma miarę 4 cm, a kąt przy niej 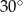 . Oblicz pole i obwód trójkąta.
. Oblicz pole i obwód trójkąta.
W trójkąt równoramienny o podstawie 12 cm i wysokości 8 cm wpisano okrąg. Oblicz promień tego okręgu.
W trójkąt równoramienny o podstawie 24 cm i wysokości 5 cm wpisano okrąg. Oblicz promień tego okręgu.
Dwusieczna kąta prostego trójkąta prostokątnego dzieli przeciwprostokątną na odcinki, o długościach  i
i 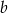 . Oblicz długości przyprostokątnych tego trójkąta.
. Oblicz długości przyprostokątnych tego trójkąta.
W trójkącie 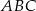 bok
bok 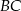 ma długość 24 cm. Oblicz obwód tego trójkąta, wiedząc, że miara kąta przy wierzchołku
ma długość 24 cm. Oblicz obwód tego trójkąta, wiedząc, że miara kąta przy wierzchołku 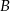 jest równa
jest równa 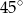 , a miara kąta przy wierzchołku
, a miara kąta przy wierzchołku 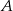 jest równa
jest równa 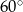 .
.
W trójkącie 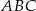 bok
bok 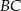 ma długość 12 cm. Oblicz obwód tego trójkąta, wiedząc, że miara kąta przy wierzchołku
ma długość 12 cm. Oblicz obwód tego trójkąta, wiedząc, że miara kąta przy wierzchołku 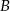 jest równa
jest równa 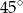 , a miara kąta przy wierzchołku
, a miara kąta przy wierzchołku 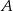 jest równa
jest równa 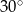 .
.

