Uzasadnij, że trójkąt równoboczny nie jest figurą środkowosymetryczną.
/Szkoła średnia/Geometria/Planimetria/Trójkąt
Trójkąt 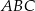 jest równoboczny. Punkt
jest równoboczny. Punkt 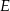 leży na wysokości
leży na wysokości 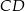 tego trójkąta oraz
tego trójkąta oraz 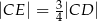 . Punkt
. Punkt 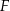 leży na boku
leży na boku 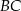 i odcinek
i odcinek 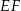 jest prostopadły do
jest prostopadły do 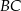 (zobacz rysunek).
(zobacz rysunek).
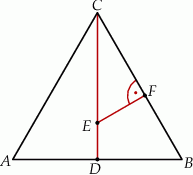
Wykaż, że 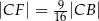 .
.
Trójkąt 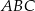 jest równoboczny. Punkt
jest równoboczny. Punkt 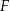 leży na wysokości
leży na wysokości 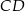 tego trójkąta oraz
tego trójkąta oraz 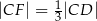 . Punkt
. Punkt 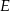 leży na boku
leży na boku 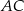 i odcinek
i odcinek 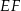 jest prostopadły do
jest prostopadły do 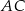 (zobacz rysunek).
(zobacz rysunek).
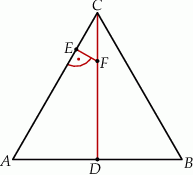
Wykaż, że 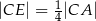 .
.
Punkt 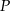 jest punktem przecięcia dwusiecznych kątów trójkąta
jest punktem przecięcia dwusiecznych kątów trójkąta 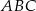 . Przez punkt
. Przez punkt 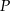 poprowadzono prostą równoległą do boku
poprowadzono prostą równoległą do boku 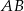 , która przecięła prostą
, która przecięła prostą 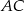 w punkcie
w punkcie 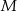 i prostą
i prostą 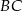 w punkcie
w punkcie 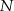 .
.
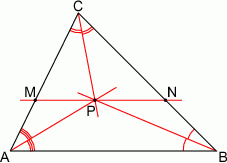
- Wykaż, że
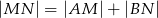 .
. - Wiedząc dodatkowo, że obwód trójkąta
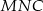 jest równy 15 cm, a długość odcinka
jest równy 15 cm, a długość odcinka 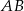 wynosi 10 cm, oblicz obwód trójkąta
wynosi 10 cm, oblicz obwód trójkąta 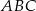 .
.
Wysokość 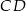 trójkąta
trójkąta 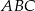 tworzy z bokami
tworzy z bokami 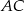 i
i 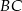 kąty o miarach równych odpowiednio
kąty o miarach równych odpowiednio 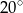 i
i 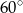 . Punkt
. Punkt 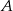 należy do odcinka
należy do odcinka 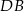 .
.
- Narysuj trójkąt
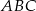 i jego wysokość
i jego wysokość 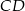 .
. - Wyznacz miary kątów trójkąta
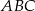 .
.
Dany jest trójkąt 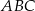 . Na boku
. Na boku 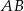 tego trójkąta obrano punkty
tego trójkąta obrano punkty 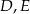 i
i 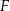 tak, że
tak, że 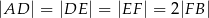 . Na bokach
. Na bokach 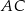 i
i 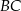 obrano – odpowiednio – punkty
obrano – odpowiednio – punkty 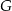 i
i 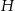 tak, że
tak, że 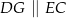 oraz
oraz 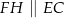 (zobacz rysunek). Wykaż, że jeżeli pole trójkąta
(zobacz rysunek). Wykaż, że jeżeli pole trójkąta 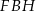 jest równe
jest równe 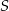 , to pole trójkąta
, to pole trójkąta 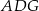 jest równe
jest równe 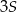 .
.
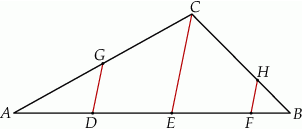
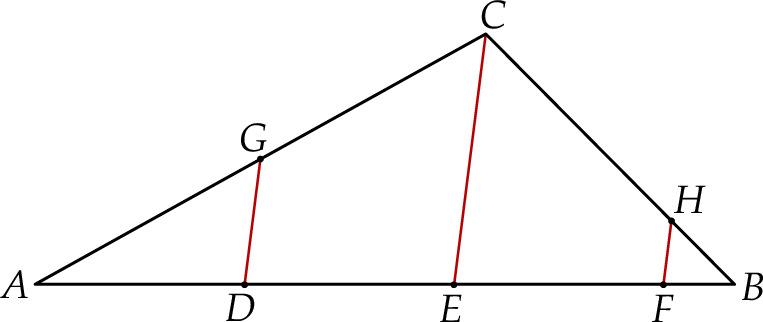
Dany jest trójkąt 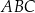 . Na boku
. Na boku 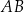 tego trójkąta obrano punkty
tego trójkąta obrano punkty 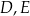 i
i 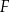 tak, że
tak, że 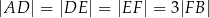 . Na bokach
. Na bokach 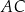 i
i 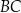 obrano – odpowiednio – punkty
obrano – odpowiednio – punkty 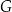 i
i 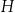 tak, że
tak, że 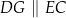 oraz
oraz 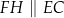 (zobacz rysunek). Wykaż, że jeżeli pole trójkąta
(zobacz rysunek). Wykaż, że jeżeli pole trójkąta 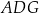 jest równe
jest równe 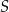 , to pole trójkąta
, to pole trójkąta 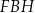 jest równe
jest równe 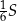 .
.
Wykaż, że jeśli  i
i 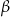 są kątami trójkąta oraz
są kątami trójkąta oraz 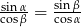 to trójkąt ten jest równoramienny lub prostokątny.
to trójkąt ten jest równoramienny lub prostokątny.
W trójkącie równoramiennym kąt przy wierzchołku ma miarę 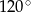 . Wyznacz stosunek długości promienia okręgu opisanego na tym trójkącie do długości promienia okręgu wpisanego w ten trójkąt.
. Wyznacz stosunek długości promienia okręgu opisanego na tym trójkącie do długości promienia okręgu wpisanego w ten trójkąt.
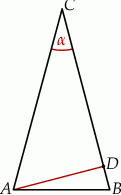
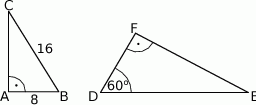
W trójkącie równoramiennym 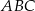 dane są
dane są 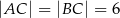 i
i 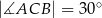 (zobacz rysunek). Oblicz wysokość
(zobacz rysunek). Oblicz wysokość 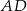 trójkąta opuszczoną z wierzchołka
trójkąta opuszczoną z wierzchołka 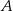 na bok
na bok 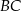 .
.
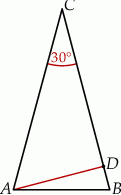
W trójkącie równoramiennym 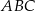 dane są
dane są 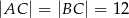 i
i 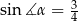 (zobacz rysunek). Oblicz wysokość
(zobacz rysunek). Oblicz wysokość 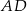 trójkąta opuszczoną z wierzchołka
trójkąta opuszczoną z wierzchołka 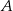 na bok
na bok 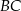 .
.
Dany jest trójkąt prostokątny, którego przyprostokątne mają długości  i
i 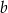 . Punkt
. Punkt 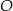 leży na przeciwprostokątnej tego trójkąta i jest środkiem okręgu stycznego do przyprostokątnych tego trójkąta (zobacz rysunek).
leży na przeciwprostokątnej tego trójkąta i jest środkiem okręgu stycznego do przyprostokątnych tego trójkąta (zobacz rysunek).
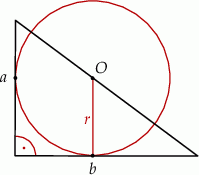
Wykaż, że promień  tego okręgu jest równy
tego okręgu jest równy 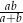 .
.
Punkt 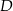 leży na boku
leży na boku 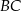 trójkąta równoramiennego
trójkąta równoramiennego 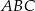 , w którym
, w którym 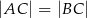 .
.
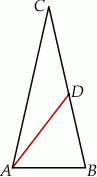
Odcinek 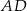 dzieli trójkąt
dzieli trójkąt 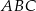 na dwa trójkąty równoramienne w taki sposób, że
na dwa trójkąty równoramienne w taki sposób, że 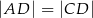 oraz
oraz 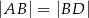 . Udowodnij, że
. Udowodnij, że 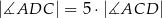 .
.
Punkt 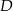 leży na boku
leży na boku 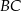 trójkąta równoramiennego, w którym
trójkąta równoramiennego, w którym 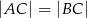 . Odcinek
. Odcinek 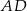 dzieli trójkąt
dzieli trójkąt 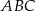 na dwa trójkąty równoramienne takie, że
na dwa trójkąty równoramienne takie, że 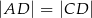 i
i 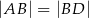 . Wykaż, że
. Wykaż, że 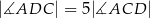 .
.
W trójkąt prostokątny 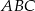 wpisano okrąg. Punkty
wpisano okrąg. Punkty 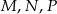 są punktami styczności okręgu odpowiednio z bokami
są punktami styczności okręgu odpowiednio z bokami 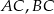 oraz
oraz 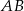 . Przeciwprostokątna
. Przeciwprostokątna 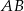 ma długość 20 cm, a długości przyprostokątnych pozostają w stosunku
ma długość 20 cm, a długości przyprostokątnych pozostają w stosunku 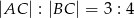 . Oblicz obwód trójkąta
. Oblicz obwód trójkąta 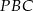 .
.
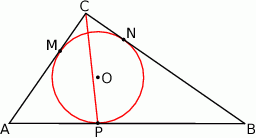
Kąty w trójkącie mają miary: 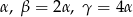 . Wykaż, że długości boków
. Wykaż, że długości boków 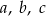 tego trójkąta spełniają równość:
tego trójkąta spełniają równość: 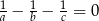 .
.
W trójkącie ostrokątnym 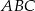 , którego pole równa się 16, boki
, którego pole równa się 16, boki 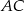 i
i 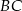 mają długości
mają długości 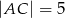 ,
, 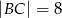 . Oblicz długość boku
. Oblicz długość boku 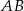 .
.
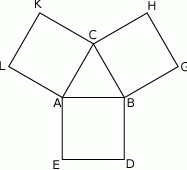
Na bokach trójkąta równobocznego 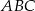 (na zewnątrz tego trójkąta) zbudowano kwadraty
(na zewnątrz tego trójkąta) zbudowano kwadraty 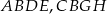 i
i 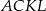 . Udowodnij, że trójkąt
. Udowodnij, że trójkąt 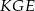 jest równoboczny.
jest równoboczny.
W trójkącie prostokątnym 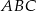 dwusieczna kąta prostego przecina przeciwprostokątną
dwusieczna kąta prostego przecina przeciwprostokątną 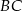 w punkcie
w punkcie 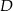 . Środek okręgu wpisanego w ten trójkąt dzieli odcinek
. Środek okręgu wpisanego w ten trójkąt dzieli odcinek 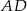 w stosunku
w stosunku 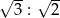 , licząc od punktu
, licząc od punktu 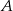 . Oblicz miary kątów ostrych trójkąta
. Oblicz miary kątów ostrych trójkąta 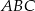 .
.
Punkty 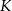 i
i 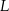 są środkami boków
są środkami boków 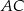 i
i 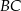 trójkąta
trójkąta 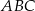 . Odcinki
. Odcinki 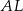 i
i 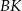 przecinają się w punkcie
przecinają się w punkcie 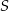 .
.
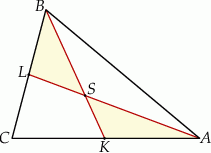
Uzasadnij, że pola trójkątów 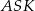 i
i 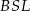 są równe.
są równe.
Punkt 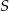 jest punktem przecięcia się wysokości trójkąta ostrokątnego
jest punktem przecięcia się wysokości trójkąta ostrokątnego 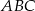 . Wykaż, że jeżeli
. Wykaż, że jeżeli 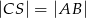 to
to 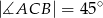 .
.
Uzasadnij, że trójkąty prostokątne 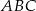 i
i 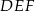 (patrz rysunek) są podobne.
(patrz rysunek) są podobne.
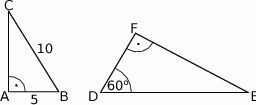
Uzasadnij, że trójkąty prostokątne 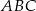 i
i 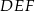 (patrz rysunek) są podobne.
(patrz rysunek) są podobne.
Środkowa trójkąta jest równa połowie boku, do którego została poprowadzona. Wykaż, że trójkąt ten jest prostokątny.
Punkt 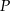 jest punktem przecięcia się wysokości trójkąta równobocznego. Jakie pole ma ten trójkąt, jeśli odcinek łączący punkt
jest punktem przecięcia się wysokości trójkąta równobocznego. Jakie pole ma ten trójkąt, jeśli odcinek łączący punkt 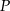 z wierzchołkiem trójkąta ma długość
z wierzchołkiem trójkąta ma długość 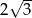 ?
?
Punkt 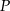 jest punktem przecięcia wysokości trójkąta równobocznego. Jaki obwód ma ten trójkąt jeśli odległość punktu
jest punktem przecięcia wysokości trójkąta równobocznego. Jaki obwód ma ten trójkąt jeśli odległość punktu 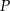 od jego boków jest równa
od jego boków jest równa 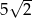 ?
?

