W trójkącie ostrokątnym 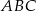 dane są
dane są 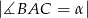 i
i 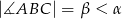 . Wykaż, że tangens kąta utworzonego przez środkową i wysokość opuszczone z wierzchołka
. Wykaż, że tangens kąta utworzonego przez środkową i wysokość opuszczone z wierzchołka 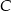 jest równy
jest równy
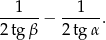
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
W trójkącie ostrokątnym 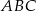 dane są
dane są 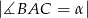 i
i 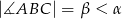 . Wykaż, że tangens kąta utworzonego przez środkową i wysokość opuszczone z wierzchołka
. Wykaż, że tangens kąta utworzonego przez środkową i wysokość opuszczone z wierzchołka 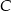 jest równy
jest równy
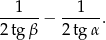
Dany jest trójkąt prostokątny 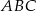 , w którym
, w którym 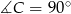 . W trójkącie tym poprowadzono wysokość
. W trójkącie tym poprowadzono wysokość 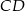 . Wykaż, że
. Wykaż, że 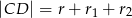 , gdzie
, gdzie 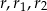 są odpowiednio długościami promieni okręgów wpisanych w trójkąty
są odpowiednio długościami promieni okręgów wpisanych w trójkąty 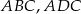 i
i 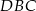 .
.
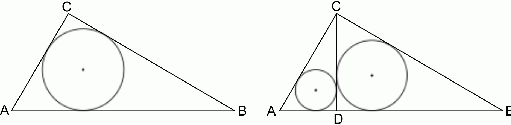
W trójkącie równoramiennym ostrokątnym 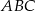 mamy dane
mamy dane 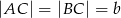 oraz
oraz 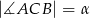 . Z wierzchołka
. Z wierzchołka 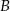 przez środek okręgu opisanego na tym trójkącie poprowadzono prostą, przecinającą bok
przez środek okręgu opisanego na tym trójkącie poprowadzono prostą, przecinającą bok 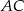 w punkcie
w punkcie 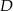 . Oblicz promień okręgu wpisanego w trójkąt
. Oblicz promień okręgu wpisanego w trójkąt 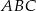 oraz długość odcinka
oraz długość odcinka 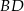 .
.
W trójkącie prostokątnym jedna z przyprostokątnych ma długość 15 cm, a przeciwprostokątna jest o 9 cm dłuższa od drugiej przyprostokątnej. Oblicz pole tego trójkąta oraz długość wysokości poprowadzonej z wierzchołka kąta prostego.
W trójkącie prostokątnym jedna z przyprostokątnych ma długość 10 cm, a przeciwprostokątna jest o 2 cm dłuższa od drugiej przyprostokątnej. Oblicz pole tego trójkąta oraz długość wysokości poprowadzonej z wierzchołka kąta prostego.
W trójkącie prostokątnym wysokość poprowadzona na przeciwprostokątną ma długość 10 cm, a promień okręgu opisanego ma długość 19 cm. Oblicz pole tego trójkąta.
Przeciwprostokątna trójkąta prostokątnego o obwodzie 40 ma długość 17. Oblicz długości przyprostokątnych tego trójkąta.
Dany jest trójkąt o bokach długości 4 (podstawa trójkąta), 5 i 6 – boki trójkąta. Przez punkt przecięcia się środkowych trójkąta prowadzimy prostą równoległą do podstawy. Oblicz obwód trójkąta którego podstawą jest ta prosta.
Oblicz sinusy kątów ostrych trójkąta prostokątnego, wiedząc, że stosunek długości promienia okręgu wpisanego do promienia okręgu opisanego na tym trójkącie jest równy 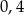 .
.
Wyznacz sinusy kątów ostrych trójkąta prostokątnego wiedząc, że stosunek promieni okręgów opisanego i wpisanego w ten trójkąt jest równy 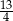 .
.
Wyznaczyć sinusy kątów ostrych trójkąta prostokątnego wiedząc, że stosunek promieni okręgów opisanego i wpisanego w ten trójkąt jest równy  .
.
Jeden z kątów ostrych trójkąta prostokątnego ma miarę  . Oblicz stosunek wysokości poprowadzonej z wierzchołka kąta prostego do promienia okręgu wpisanego w ten trójkąt.
. Oblicz stosunek wysokości poprowadzonej z wierzchołka kąta prostego do promienia okręgu wpisanego w ten trójkąt.
W trójkąt równoboczny o boku długości 6 cm wpisano kwadrat. Oblicz pole tego kwadratu.
Znaleźć pole kwadratu wpisanego w trójkąt równoboczny o boku 4 cm.
W trójkąt prostokątny 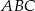 o przyprostokątnych długości
o przyprostokątnych długości 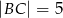 i
i 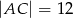 wpisano okrąg. Oblicz długość odcinka łączącego punkty wspólne okręgu wpisanego z bokami
wpisano okrąg. Oblicz długość odcinka łączącego punkty wspólne okręgu wpisanego z bokami 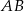 i
i 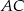 .
.
Oblicz długości boków trójkąta prostokątnego wiedząc, że długości przyprostokątnych różnią się o 9 cm, a jego pole jest równe 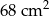 .
.
Oblicz obwód trójkąta prostokątnego o polu powierzchni równym 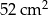 , wiedząc, że długości jego przyprostokątnych różnią się o 5 cm.
, wiedząc, że długości jego przyprostokątnych różnią się o 5 cm.
Oblicz długości boków trójkąta prostokątnego o polu powierzchni równym 5, wiedząc, że długości jego przyprostokątnych różnią się o 3.
Pole trójkąta prostokątnego jest równe 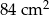 . Jedna przyprostokątna jest o 17 cm dłuższa od drugiej. Oblicz długość przeciwprostokątnej tego trójkąta.
. Jedna przyprostokątna jest o 17 cm dłuższa od drugiej. Oblicz długość przeciwprostokątnej tego trójkąta.
Oblicz długości boków trójkąta prostokątnego o polu powierzchni równym 20, wiedząc, że długości jego przyprostokątnych różnią się o 6.
Oblicz obwód trójkąta prostokątnego o polu powierzchni równym 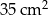 , wiedząc, że długości jego przyprostokątnych różnią się o 3 cm.
, wiedząc, że długości jego przyprostokątnych różnią się o 3 cm.
Pole trójkąta prostokątnego jest równe 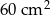 . Jedna przyprostokątna jest o 7 cm dłuższa od drugiej. Oblicz długość przeciwprostokątnej tego trójkąta.
. Jedna przyprostokątna jest o 7 cm dłuższa od drugiej. Oblicz długość przeciwprostokątnej tego trójkąta.
Na boku 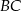 trójkąta
trójkąta 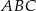 wybrano punkt
wybrano punkt 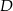 tak, by
tak, by 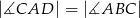 . Odcinek
. Odcinek 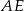 jest dwusieczną kąta
jest dwusieczną kąta 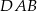 . Udowodnij, że
. Udowodnij, że 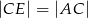 .
.
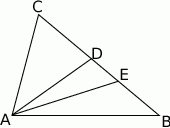
Miary kątów trójkąta są w stosunku 1:2:3. Obwód koła opisanego na tym trójkącie jest równy 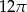 . Oblicz pole tego trójkąta.
. Oblicz pole tego trójkąta.
Na bokach 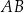 i
i 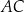 trójkąta
trójkąta 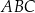 wybrano odpowiednio punkty
wybrano odpowiednio punkty 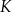 i
i 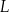 w ten sposób, że
w ten sposób, że 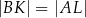 . Punkt
. Punkt 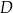 jest środkiem odcinka
jest środkiem odcinka 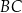 . Przez punkty
. Przez punkty 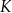 i
i 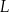 poprowadzono proste równoległe do
poprowadzono proste równoległe do 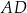 , które wyznaczyły na boku
, które wyznaczyły na boku 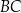 punkty
punkty 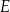 i
i 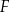 odpowiednio (zobacz rysunek). Wykaż, że jeżeli
odpowiednio (zobacz rysunek). Wykaż, że jeżeli 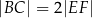 , to
, to 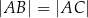 .
.

Udowodnij, że w trójkącie prostokątnym dwusieczna kąta prostego dzieli na połowy kąt zawarty między środkową, a wysokością opuszczoną z wierzchołka kąta prostego.
W trójkącie prostokątnym dany jest kąt ostry o mierze  i pole
i pole 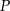 tego trójkąta. Obliczyć długość środkowej poprowadzonej z wierzchołka kąta prostego.
tego trójkąta. Obliczyć długość środkowej poprowadzonej z wierzchołka kąta prostego.
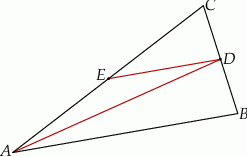
Punkty 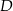 i
i 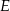 są środkami boków
są środkami boków 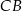 i
i 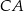 trójkąta
trójkąta 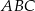 (zobacz rysunek). Wykaż, że odległość punktu
(zobacz rysunek). Wykaż, że odległość punktu 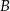 od prostej
od prostej 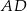 jest dwa razy większa od odległości punktu
jest dwa razy większa od odległości punktu 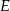 od prostej
od prostej 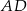 .
.
W trójkącie 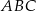 długości boków
długości boków 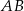 i
i 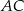 są odpowiednio równe 4 i 6, a długość środkowej
są odpowiednio równe 4 i 6, a długość środkowej 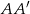 jest równa
jest równa 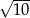 . Oblicz długość boku
. Oblicz długość boku 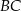 .
.
Oblicz pole trójkąta równoramiennego 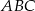 , w którym
, w którym 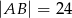 i
i 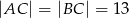 .
.
