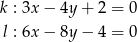Określ wzajemne położenie prostych 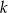 i
i 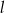 o równaniach
o równaniach
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Określ wzajemne położenie prostych 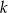 i
i 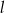 o równaniach
o równaniach
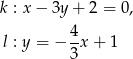
Środek okręgu przechodzącego przez punkty 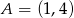 i
i 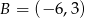 leży na osi
leży na osi 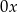 .
.
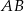 i oddalonej od początku układu współrzędnych o
i oddalonej od początku układu współrzędnych o 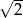 .
.Prosta 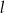 , na której leży punkt
, na której leży punkt 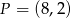 , tworzy z dodatnimi półosiami układu współrzędnych trójkąt prostokątny o polu równym 36. Wyznacz równanie prostej
, tworzy z dodatnimi półosiami układu współrzędnych trójkąt prostokątny o polu równym 36. Wyznacz równanie prostej 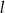 .
.
Prosta 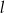 , na której leży punkt
, na której leży punkt 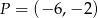 , tworzy z ujemnymi półosiami układu współrzędnych trójkąt prostokątny o polu równym 24. Wyznacz równanie prostej
, tworzy z ujemnymi półosiami układu współrzędnych trójkąt prostokątny o polu równym 24. Wyznacz równanie prostej 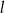 .
.
Dane są punkty 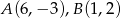 oraz
oraz 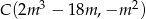 . Wyznacz wszystkie wartości
. Wyznacz wszystkie wartości 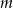 , dla których proste
, dla których proste 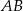 i
i 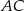 są prostopadłe.
są prostopadłe.
Dane są punkty 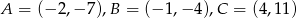 . Wykaż, że punkty te są współliniowe
. Wykaż, że punkty te są współliniowe
Znajdź równanie prostej, zawierającą dwusieczną tego kąta, utworzonego przez proste 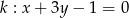 oraz
oraz 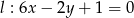 , do obszaru którego należy punkt
, do obszaru którego należy punkt 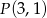 .
.
Proste o równaniach: 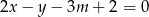 i
i 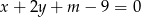 przecinają się w punkcie
przecinają się w punkcie 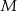 . Dla jakich wartości
. Dla jakich wartości 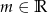 punkt
punkt 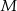 należy do prostej o równaniu
należy do prostej o równaniu 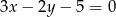 .
.
Dana jest prosta 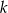 o równaniu parametrycznym
o równaniu parametrycznym 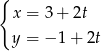 dla
dla 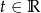 . Znajdź równanie parametryczne:
. Znajdź równanie parametryczne:
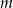 równoległej do prostej
równoległej do prostej 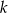 , przechodzącej przez punkt
, przechodzącej przez punkt 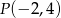 .
.  prostopadłej do prostej
prostopadłej do prostej 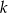 , przechodzącej przez punkt
, przechodzącej przez punkt 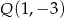 .
.Oblicz odległość punktu 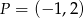 od prostej o równaniu
od prostej o równaniu 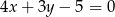 .
.
Dany jest punkt 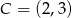 i prosta o równaniu
i prosta o równaniu 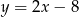 będąca symetralną odcinka
będąca symetralną odcinka 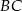 . Wyznacz współrzędne punktu
. Wyznacz współrzędne punktu 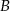 . Wykonaj obliczenia uzasadniające odpowiedź.
. Wykonaj obliczenia uzasadniające odpowiedź.
Różnica współczynników kierunkowych dwóch prostych jest równa różnicy odwrotności tych współczynników. Uzasadnij, że te proste są prostopadłe albo równoległe.
Dwie proste mają tę własności, że różnica współczynnika kierunkowego i jego odwrotności w przypadku każdej z tych prostych jest taka sama. Uzasadnij, że te proste są prostopadłe albo równoległe.
Wyznacz równanie prostej, która przecina oś 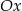 pod kątem
pod kątem 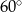 , a oś
, a oś 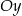 w punkcie
w punkcie 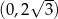 .
.
Znaleźć równania dwusiecznych kątów wyznaczonych przez proste o równaniach 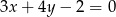 i
i 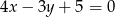 .
.
Znaleźć równania dwusiecznych kątów wyznaczonych przez proste o równaniach 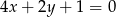 i
i 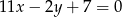 .
.
Dla jakich wartości parametru 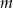 proste
proste 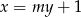 oraz
oraz 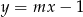 przecinają się w jednym punkcie, który leży poniżej prostej
przecinają się w jednym punkcie, który leży poniżej prostej 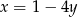 ?
?
Prosta 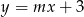 tworzy z dodatnimi półosiami układu współrzędnych trójkąt o polu 7. Wyznacz
tworzy z dodatnimi półosiami układu współrzędnych trójkąt o polu 7. Wyznacz 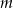 .
.
Prosta 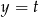 przecina proste
przecina proste 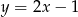 i
i 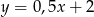 odpowiednio w punktach
odpowiednio w punktach 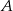 i
i 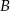 .
.
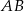 jako funkcję zmiennej
jako funkcję zmiennej 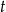 .
. 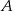 i
i 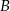 , aby długość odcinka
, aby długość odcinka 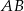 była równa 3.
była równa 3.Prosta 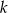 jest wykresem funkcji
jest wykresem funkcji 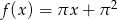 .
.
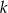 z wykresem funkcji
z wykresem funkcji 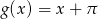 .
. 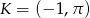 i równoległej do prostej
i równoległej do prostej 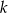 .
.Wyznacz równanie prostej równoległej do prostej 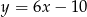 przechodzącej przez punkt
przechodzącej przez punkt 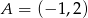 oraz równanie prostej prostopadłej do tych prostych przechodzącej przez punkt
oraz równanie prostej prostopadłej do tych prostych przechodzącej przez punkt 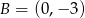 .
.
Napisz równanie prostej równoległej do prostej o równaniu 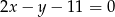 i przechodzącej przez punkt
i przechodzącej przez punkt 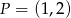 .
.
Wyznacz odległość między prostymi