Punkt 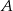 jest punktem wspólnym prostych prostopadłych
jest punktem wspólnym prostych prostopadłych 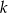 i
i 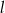 o równaniach
o równaniach 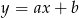 oraz
oraz 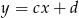 . Wykaż, że jeżeli
. Wykaż, że jeżeli 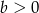 i
i 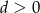 , to druga współrzędna punktu
, to druga współrzędna punktu 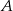 jest liczbą dodatnią.
jest liczbą dodatnią.
/Szkoła średnia/Geometria/Geometria analityczna/Równanie prostej
Wierzchołek kąta znajduje się w punkcie 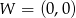 , jedno z jego ramion leży na prostej
, jedno z jego ramion leży na prostej 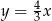 , a drugie ramię przechodzi przez punkt
, a drugie ramię przechodzi przez punkt 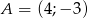 . Punkt
. Punkt 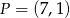 należy do wnętrza tego kąta. Sprawdź rachunkowo, czy punkt
należy do wnętrza tego kąta. Sprawdź rachunkowo, czy punkt 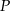 leży na dwusiecznej tego kąta.
leży na dwusiecznej tego kąta.
Wyznacz odległość między prostymi 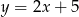 i
i 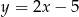 .
.
Wyznacz równanie prostej przechodzącej przez punkty 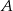 i
i 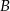 jeżeli
jeżeli 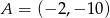 i
i 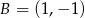 .
.
Wyznacz równanie prostej przechodzącej przez punkty 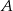 i
i 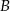 jeżeli
jeżeli 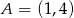 i
i 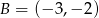 .
.
Zapisz równanie ogólne i kierunkowe prostej 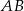 , jeśli
, jeśli 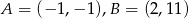 .
.
Zapisz równanie ogólne i kierunkowe prostej 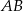 , jeśli
, jeśli 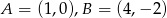 .
.
Zapisz równanie ogólne i kierunkowe prostej 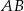 , jeśli
, jeśli 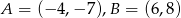 .
.
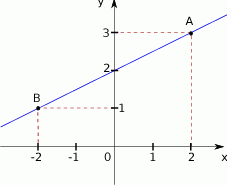
Na płaszczyźnie dane są punkty 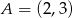 i
i 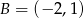 (patrz rysunek). Zbadaj, czy punkty
(patrz rysunek). Zbadaj, czy punkty 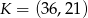 i
i 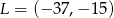 leżą po tej samej stronie prostej
leżą po tej samej stronie prostej 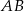 . Podaj odpowiedź i jej uzasadnienie.
. Podaj odpowiedź i jej uzasadnienie.
Początkowe ramię kąta  pokrywa się z dodatnią półosią osi odciętych, a na końcowym ramieniu tego kąta leży punkt
pokrywa się z dodatnią półosią osi odciętych, a na końcowym ramieniu tego kąta leży punkt 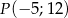 . Oblicz wartość wyrażenia:
. Oblicz wartość wyrażenia: 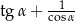 .
.
Początkowe ramię kąta  pokrywa się z dodatnią półosią osi odciętych, a na końcowym ramieniu tego kąta leży punkt
pokrywa się z dodatnią półosią osi odciętych, a na końcowym ramieniu tego kąta leży punkt 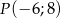 . Oblicz wartość wyrażenia:
. Oblicz wartość wyrażenia: 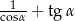 .
.
Określ wzajemne położenie prostych 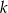 i
i 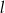 o równaniach
o równaniach
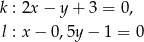
Oblicz miarę kąta ostrego, którego ramiona są zawarte w prostych o równaniach 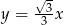 i
i 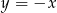 .
.
Oblicz miarę kąta ostrego, którego ramiona są zawarte w prostych o równaniach 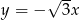 i
i 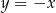 .
.
W układzie współrzędnych są dane punkty 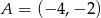 ,
, 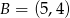 .
.
- Oblicz odległość punktu
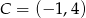 od prostej przechodzącej przez punkty
od prostej przechodzącej przez punkty 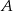 i
i 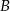 .
. - Uzasadnij, że jeśli
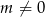 , to punkty
, to punkty 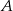 ,
, 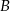 oraz punkt
oraz punkt 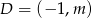 są wierzchołkami trójkąta.
są wierzchołkami trójkąta.
Jaką figurę na płaszczyźnie określa podane równanie parametryczne:
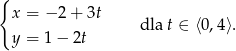
Jaką figurę na płaszczyźnie określa podane równanie parametryczne:
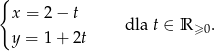
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 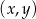 , dane są proste
, dane są proste 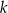 oraz
oraz 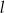 o równaniach
o równaniach
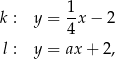
gdzie  jest pewną liczbą rzeczywistą. Proste
jest pewną liczbą rzeczywistą. Proste 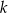 i
i 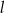 są prostopadłe. Wyznacz ich punkt przecięcia.
są prostopadłe. Wyznacz ich punkt przecięcia.
Określ wzajemne położenie prostych 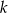 i
i 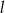 o równaniach
o równaniach
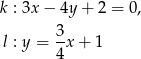
Wyznacz te wartości parametru 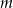 , dla których punkt przecięcia się prostych o równaniach
, dla których punkt przecięcia się prostych o równaniach 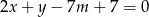 i
i 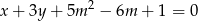 należy do 3 ćwiartki układu współrzędnych.
należy do 3 ćwiartki układu współrzędnych.
W układzie współrzędnych są dane punkty 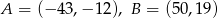 . Prosta
. Prosta 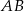 przecina oś
przecina oś 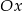 w punkcie
w punkcie 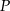 . Oblicz pierwszą współrzędną punktu
. Oblicz pierwszą współrzędną punktu 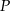 .
.
Dane są punkty 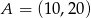 i
i 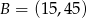 . Wyznacz współrzędne punktu przecięcia prostej
. Wyznacz współrzędne punktu przecięcia prostej 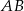 z osią
z osią 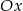 .
.
W układzie współrzędnych są dane punkty 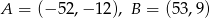 . Prosta
. Prosta 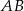 przecina oś
przecina oś 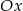 w punkcie
w punkcie 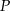 . Oblicz pierwszą współrzędną punktu
. Oblicz pierwszą współrzędną punktu 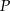 .
.
Wykaż, że cosinus kąta przecięcia się wykresów funkcji 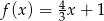 i
i 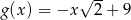 jest równy
jest równy 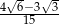 .
.
Zapisz równanie prostej przechodzącej przez punkt 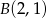 i prostopadłej do prostej danej równaniem
i prostopadłej do prostej danej równaniem 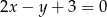 .
.
Wyznacz równanie prostej prostopadłej do prostej 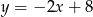 przechodzącej przez punkt
przechodzącej przez punkt 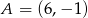 .
.
Zapisz równanie prostej przechodzącej przez punkt 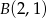 i prostopadłej do prostej danej równaniem
i prostopadłej do prostej danej równaniem 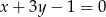 .
.
Wyznacz równanie prostej prostopadłej do prostej o równaniu 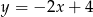 przecinającej oś
przecinającej oś 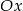 w punkcie o odciętej 4.
w punkcie o odciętej 4.
Wyznacz równanie prostej prostopadłej do prostej o równaniu 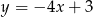 przechodzącej przez punkt
przechodzącej przez punkt 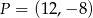 .
.
Sprawdź czy proste  i
i 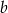 są równoległe, jeśli prosta
są równoległe, jeśli prosta  przecina oś
przecina oś  w punkcie
w punkcie 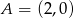 , oś
, oś 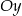 w punkcie
w punkcie 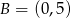 , a prosta
, a prosta 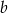 przecina oś
przecina oś 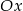 w punkcie
w punkcie 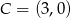 i oś
i oś 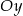 w punkcie
w punkcie 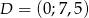 .
.
Proste o równaniach 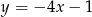 i
i 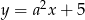 są prostopadłe. Wyznacz liczbę
są prostopadłe. Wyznacz liczbę  .
.
Proste o równaniach 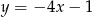 i
i 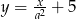 są prostopadłe. Wyznacz liczbę
są prostopadłe. Wyznacz liczbę  .
.
Proste o równaniach 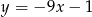 i
i 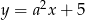 są prostopadłe. Wyznacz liczbę
są prostopadłe. Wyznacz liczbę  .
.
Dane są proste o równaniach 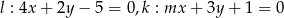 . Wyznacz parametr
. Wyznacz parametr 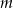 , tak aby te proste były prostopadłe.
, tak aby te proste były prostopadłe.

