Wykaż, że punkt 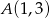 leży na dwusiecznej kąta między prostymi
leży na dwusiecznej kąta między prostymi 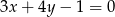 i
i 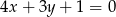 . Napisz równanie tej dwusiecznej.
. Napisz równanie tej dwusiecznej.
/Szkoła średnia/Geometria/Geometria analityczna/Równanie prostej
Dana jest funkcja 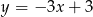 . Podaj równanie prostej prostopadłej i prostej równoległej do danej prostej, do których należy punkt
. Podaj równanie prostej prostopadłej i prostej równoległej do danej prostej, do których należy punkt 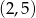 . Wykonaj rysunek do zadania.
. Wykonaj rysunek do zadania.
Dana jest funkcja 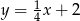 . Podaj równanie prostej prostopadłej i prostej równoległej do danej prostej, do których należy punkt
. Podaj równanie prostej prostopadłej i prostej równoległej do danej prostej, do których należy punkt 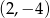 . Wykonaj rysunek do zadania.
. Wykonaj rysunek do zadania.
Prosta 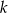 przechodzi przez punkty
przechodzi przez punkty 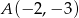 i
i 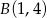 . Wyznacz równania prostej
. Wyznacz równania prostej 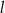 prostopadłej do
prostopadłej do 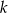 i prostej
i prostej 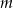 równoległej do
równoległej do 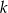 , jeżeli każda z nich przechodzi przez punkt
, jeżeli każda z nich przechodzi przez punkt 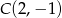 .
.
Dany jest ciąg 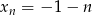 dla
dla 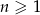 . Ciąg
. Ciąg 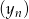 ma tę własność, że dla każdego
ma tę własność, że dla każdego 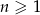 punkty o współrzędnych
punkty o współrzędnych 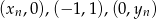 leżą na jednej prostej. Wyznacz wzór ogólny ciągu
leżą na jednej prostej. Wyznacz wzór ogólny ciągu 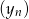 .
.
Wyznacz punkt wspólny symetralnej odcinka 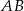 , gdzie
, gdzie 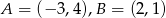 , oraz osi
, oraz osi 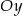 .
.
Dane są punkty 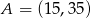 i
i 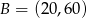 . Wyznacz współrzędne punktu przecięcia prostej
. Wyznacz współrzędne punktu przecięcia prostej 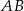 z osią
z osią 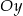 .
.
Punkt 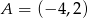 oraz
oraz 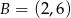 są symetryczne względem prostej
są symetryczne względem prostej  . Wyznacz równanie prostej
. Wyznacz równanie prostej  .
.
Punkt 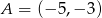 oraz
oraz 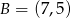 są symetryczne względem prostej
są symetryczne względem prostej  . Wyznacz równanie prostej
. Wyznacz równanie prostej  .
.
Dla jakich wartości parametru 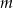 punkt przecięcia się prostych
punkt przecięcia się prostych 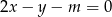 i
i 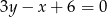 należy do prostej
należy do prostej 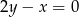 . Podaj współrzędne tego punktu i oblicz jego odległość od prostej
. Podaj współrzędne tego punktu i oblicz jego odległość od prostej 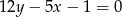 .
.
Określ wzajemne położenie prostych
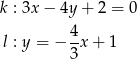
Wyznacz odległość między równoległymi prostymi:
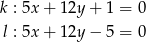
Dla jakich wartości parametru  odległość punktu
odległość punktu 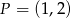 od prostej
od prostej 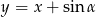 jest mniejsza lub równa
jest mniejsza lub równa 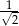 .
.
Zbadaj dla jakich wartości parametru 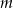 punkt przecięcia się prostych
punkt przecięcia się prostych 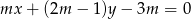 i
i 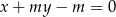 należy do prostokąta o wierzchołkach
należy do prostokąta o wierzchołkach 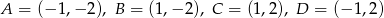 ?
?
Dany jest punkt 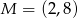 . Wyznacz równanie takiej prostej
. Wyznacz równanie takiej prostej 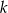 , do której należy punkt
, do której należy punkt 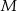 , że na ujemnej półosi
, że na ujemnej półosi 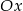 i dodatniej półosi
i dodatniej półosi 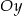 układu
układu 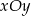 prosta ta wyznacza odcinki
prosta ta wyznacza odcinki 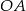 i
i 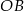 , których suma długości jest równa 6. Oblicz obwód trójkąta
, których suma długości jest równa 6. Oblicz obwód trójkąta 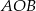 .
.
Wyznacz równanie prostej przechodzącej przez punkt 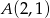 i tworzącej z prostą
i tworzącej z prostą 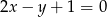 kąt o mierze
kąt o mierze 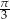 .
.
Wyznacz równanie symetralnej odcinka o końcach 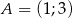 i
i 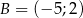 .
.
Wyznacz równanie symetralnej odcinka o końcach 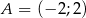 i
i 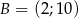 .
.
Wyznacz równanie symetralnej odcinka o końcach 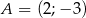 i
i 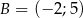 .
.
Wyznacz równanie symetralnej odcinka o końcach 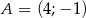 i
i 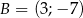 .
.
Wyznacz równanie symetralnej odcinka 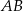 , gdzie
, gdzie 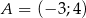 i
i 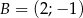 .
.
Proste 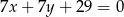 i
i 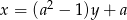 przecinają się pod kątem
przecinają się pod kątem 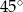 . Wyznacz liczbę
. Wyznacz liczbę  .
.
Wyznacz odległość punktu 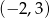 od prostej o równaniu
od prostej o równaniu 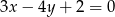 .
.
Dla jakich wartości parametru 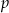 proste
proste 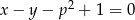 i
i 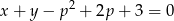 przecinają się w punkcie należącym do wnętrza prostokąta o wierzchołkach
przecinają się w punkcie należącym do wnętrza prostokąta o wierzchołkach 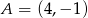 ,
, 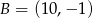 ,
, 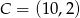 ,
, 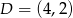 ?
?
Oblicz dla jakich wartości parametrów 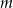 i
i  proste o równaniach:
proste o równaniach: 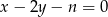 i
i 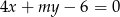 są dwiema różnymi prostymi równoległymi.
są dwiema różnymi prostymi równoległymi.
Wyznacz odległość punktu 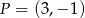 od prostej o równaniu
od prostej o równaniu 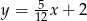 .
.

