Oblicz największą wartość wielomianu 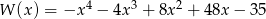 .
.
/Szkoła średnia/Funkcje/Wielomiany/Przebieg zmienności
Dana jest funkcja 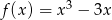 dla
dla 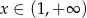 . Zbadaj na podstawie definicji monotoniczność tej funkcji w przedziale
. Zbadaj na podstawie definicji monotoniczność tej funkcji w przedziale 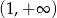 .
.
Wyznacz maksymalne przedziały monotoniczności funkcji 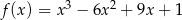 .
.
Wyznacz maksymalne przedziały monotoniczności funkcji 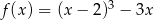 .
.
Wyznacz przedziały monotoniczności funkcji 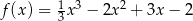 .
.
Wyznacz najmniejszą 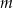 i największą
i największą 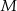 wartość funkcji
wartość funkcji 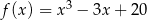 w przedziale
w przedziale 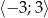 .
.
Wyznacz zbiór wartości funkcji 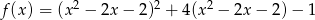 .
.
Oblicz najmniejszą wartość wielomianu 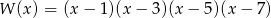 .
.
Wyznacz przedziały monotoniczności funkcji 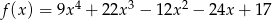 .
.
Wyznacz wszystkie argumenty  , w których funkcja
, w których funkcja 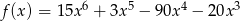 ma ekstrema lokalne.
ma ekstrema lokalne.
Wyznacz wartość największą i najmniejszą funkcji 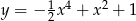 w przedziale
w przedziale 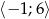 .
.
Funkcja 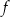 jest określona wzorem
jest określona wzorem
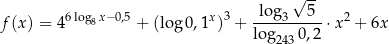
dla każdej liczby ![[ ] x ∈ 1,3 2](https://img.zadania.info/zad/5459831/HzadT2x.png) . Wyznacz zbiór wartości funkcji
. Wyznacz zbiór wartości funkcji 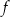 .
.
Wykaż, że funkcja 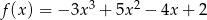 nie ma ekstremum.
nie ma ekstremum.
Wyznacz te argumenty, dla których funkcja 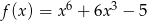 osiąga wartość najmniejszą.
osiąga wartość najmniejszą.
Wyznacz ekstrema lokalne funkcji 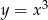 .
.
Wyznacz ekstrema lokalne funkcji 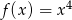 .
.
Wyznacz zbiór wartości funkcji 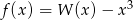 , gdzie
, gdzie 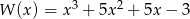 .
.
Funkcja 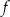 jest określona wzorem
jest określona wzorem 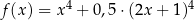 dla każdego
dla każdego 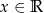 . Oblicz najmniejszą wartość tej funkcji.
. Oblicz najmniejszą wartość tej funkcji.
Wyznacz wszystkie wartości parametru 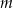 , dla których funkcja
, dla których funkcja 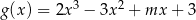 ma ekstremum lokalne równe 10.
ma ekstremum lokalne równe 10.
Dla każdej liczby rzeczywistej  obliczamy różnicę sześcianów liczb: o 1 mniejszej od
obliczamy różnicę sześcianów liczb: o 1 mniejszej od  oraz o 2 większej od
oraz o 2 większej od  . Zapisz wzór otrzymanej w ten sposób funkcji i wyznacz jej wartość największą.
. Zapisz wzór otrzymanej w ten sposób funkcji i wyznacz jej wartość największą.
Dla jakiej wartości parametru 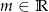 funkcja
funkcja 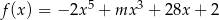 ma ekstremum w punkcie
ma ekstremum w punkcie 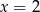 ?
?
Funkcja 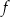 jest określona wzorem
jest określona wzorem
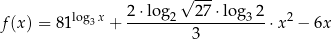
dla każdej liczby dodatniej  .
.
-
Wykaż, że dla każdej liczby dodatniej
 wzór funkcji
wzór funkcji 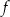 można równoważnie przekształcić do postaci
można równoważnie przekształcić do postaci 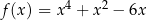 .
. -
Oblicz najmniejszą wartość funkcji
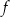 określonej dla każdej liczby dodatniej
określonej dla każdej liczby dodatniej  .
.
Funkcja 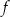 jest określona wzorem
jest określona wzorem
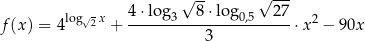
dla każdej liczby dodatniej  .
.
-
Wykaż, że dla każdej liczby dodatniej
 wzór funkcji
wzór funkcji 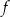 można równoważnie przekształcić do postaci
można równoważnie przekształcić do postaci 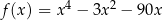 .
. -
Oblicz najmniejszą wartość funkcji
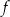 określonej dla każdej liczby dodatniej
określonej dla każdej liczby dodatniej  .
.
Wyznacz ekstrema lokalne funkcji 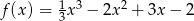 .
.

