Iloczyn  początkowych wyrazów ciągu geometrycznego wyraża się wzorem
początkowych wyrazów ciągu geometrycznego wyraża się wzorem 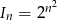 . Oblicz pierwszy wyraz tego ciągu i jego iloraz.
. Oblicz pierwszy wyraz tego ciągu i jego iloraz.
/Szkoła średnia/Ciągi
Niech 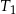 będzie trójkątem równobocznym o boku długości
będzie trójkątem równobocznym o boku długości  . Konstruujemy kolejno trójkąty równoboczne
. Konstruujemy kolejno trójkąty równoboczne 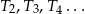 takie, że bok kolejnego trójkąta jest równy wysokości poprzedniego trójkąta. Oblicz sumę pól wszystkich tak utworzonych trójkątów
takie, że bok kolejnego trójkąta jest równy wysokości poprzedniego trójkąta. Oblicz sumę pól wszystkich tak utworzonych trójkątów 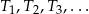 .
.
Wyznacz iloraz nieskończonego, zbieżnego ciągu geometrycznego, w którym pierwszy wyraz jest równy 6, a suma wszystkich wyrazów tego ciągu stanowi  sumy ich kwadratów.
sumy ich kwadratów.
Ciąg 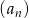 jest określony wzorem
jest określony wzorem 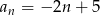 . Uzasadnij (na podstawie definicji) że ciąg
. Uzasadnij (na podstawie definicji) że ciąg 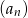 jest arytmetyczny.
jest arytmetyczny.
Wykaż, że ciąg o wzorze ogólnym 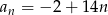 , gdzie
, gdzie 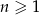 , jest ciągiem arytmetycznym.
, jest ciągiem arytmetycznym.
Dany jest ciąg 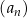 określony wzorem ogólnym
określony wzorem ogólnym 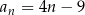 dla każdej liczby naturalnej
dla każdej liczby naturalnej 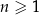 . Wykaż, że ciąg
. Wykaż, że ciąg 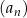 jest arytmetyczny.
jest arytmetyczny.
Wykaż, że ciąg liczbowy o wyrazie ogólnym 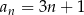 , gdzie
, gdzie 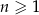 , jest ciągiem arytmetycznym.
, jest ciągiem arytmetycznym.
Wykaż, że ciąg o wzorze ogólnym 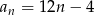 , gdzie
, gdzie 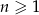 , jest ciągiem arytmetycznym.
, jest ciągiem arytmetycznym.
Wykaż, że ciąg liczbowy o wyrazie ogólnym 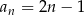 , gdzie
, gdzie 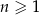 , jest ciągiem arytmetycznym.
, jest ciągiem arytmetycznym.
W ciągu geometrycznym przez 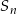 oznaczamy sumę
oznaczamy sumę  początkowych wyrazów tego ciągu, dla liczb naturalnych
początkowych wyrazów tego ciągu, dla liczb naturalnych 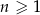 . Wiadomo, że dla pewnego ciągu geometrycznego:
. Wiadomo, że dla pewnego ciągu geometrycznego: 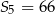 i
i 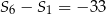 . Wyznacz iloraz i ósmy wyraz tego ciągu.
. Wyznacz iloraz i ósmy wyraz tego ciągu.
Wyznacz wszystkie wartości 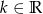 , dla których pierwiastki wielomianu
, dla których pierwiastki wielomianu 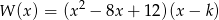 są trzema kolejnymi wyrazami rosnącego ciągu geometrycznego.
są trzema kolejnymi wyrazami rosnącego ciągu geometrycznego.
Oblicz granicę ciągu
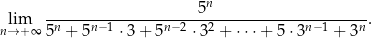
W ciągu arytmetycznym suma pierwszego i trzeciego wyrazu jest równa 2, a iloraz pierwszego i czwartego jest równy 1.
- Napisz wzór ogólny ciągu oraz wzór na sumę
 początkowych wyrazów tego ciągu.
początkowych wyrazów tego ciągu. - Wyznacz
 , dla których suma
, dla których suma  kolejnych, początkowych wyrazów ciągu jest mniejsza od 50.
kolejnych, początkowych wyrazów ciągu jest mniejsza od 50.
Iloczyn drugiego i czwartego wyrazu ciągu geometrycznego o wyrazach dodatnich jest równy 9. Oblicz iloczyn pięciu początkowych kolejnych wyrazów tego ciągu.
Ciąg 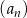 , określony dla każdej liczby naturalnej
, określony dla każdej liczby naturalnej 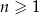 , jest geometryczny i ma wszystkie wyrazy dodatnie. Ponadto
, jest geometryczny i ma wszystkie wyrazy dodatnie. Ponadto 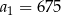 i
i 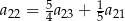 . Ciąg
. Ciąg 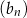 , określony dla każdej liczby naturalnej
, określony dla każdej liczby naturalnej 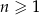 , jest arytmetyczny. Suma wszystkich wyrazów ciągu
, jest arytmetyczny. Suma wszystkich wyrazów ciągu 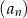 jest równa sumie dwudziestu pięciu początkowych kolejnych wyrazów ciągu
jest równa sumie dwudziestu pięciu początkowych kolejnych wyrazów ciągu 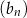 . Ponadto
. Ponadto 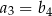 . Oblicz
. Oblicz 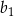 .
.
W skończonym ciągu geometrycznym 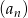 wyraz pierwszy jest równy 3, a wyraz ostatni 768. Wiedząc, że suma wszystkich wyrazów wynosi 1533, oblicz iloraz tego ciągu.
wyraz pierwszy jest równy 3, a wyraz ostatni 768. Wiedząc, że suma wszystkich wyrazów wynosi 1533, oblicz iloraz tego ciągu.
W skończonym ciągu geometrycznym 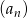 wyraz pierwszy jest równy 2, a wyraz ostatni 39 366. Wiedząc, że suma wszystkich wyrazów wynosi 59 048, oblicz iloraz tego ciągu.
wyraz pierwszy jest równy 2, a wyraz ostatni 39 366. Wiedząc, że suma wszystkich wyrazów wynosi 59 048, oblicz iloraz tego ciągu.
W trójkącie prostokątnym jedna z przyprostokątnych jest średnią arytmetyczną drugiej przyprostokątnej i przeciwprostokątnej. Oblicz sinusy kątów ostrych tego trójkąta.
W trójkącie prostokątnym stosunek różnicy długości przyprostokątnych do długości przeciwprostokątnej jest równy 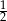 . Oblicz cosinusy kątów ostrych tego trójkąta.
. Oblicz cosinusy kątów ostrych tego trójkąta.
W trójkącie prostokątnym stosunek sumy długości przyprostokątnych do długości przeciwprostokątnej jest równy  . Oblicz cosinusy kątów ostrych tego trójkąta.
. Oblicz cosinusy kątów ostrych tego trójkąta.
Cztery liczby tworzą ciąg geometryczny, przy czym suma pierwszej i czwartej jest równa 27, a iloczyn drugiej i trzeciej jest równy 72. Wyznacz te liczby.
Cztery liczby tworzą ciąg geometryczny, przy czym suma pierwszej i czwartej jest równa 52, a iloczyn drugiej i trzeciej jest równy 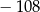 . Wyznacz te liczby.
. Wyznacz te liczby.
Trzy początkowe wyrazy malejącego ciągu arytmetycznego są pierwiastkami wielomianu 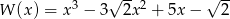 , a jednym z nich jest
, a jednym z nich jest 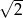 .
.
- Znajdź pierwszy wyraz tego ciągu.
- Oblicz sumę
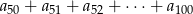 .
.
Wyznacz wszystkie wartości  , dla których trzy liczby:
, dla których trzy liczby: 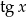 ,
, 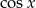 ,
, 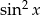 , tworzą ciąg geometryczny (w podanej kolejności).
, tworzą ciąg geometryczny (w podanej kolejności).
W ciągu geometrycznym przez 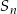 oznaczamy sumę
oznaczamy sumę  początkowych wyrazów tego ciągu, dla liczb naturalnych
początkowych wyrazów tego ciągu, dla liczb naturalnych 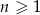 . Wiadomo, że dla pewnego ciągu geometrycznego:
. Wiadomo, że dla pewnego ciągu geometrycznego: 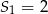 i
i 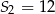 . Wyznacz iloraz i piąty wyraz tego ciągu.
. Wyznacz iloraz i piąty wyraz tego ciągu.
W ciągu geometrycznym przez 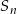 oznaczamy sumę
oznaczamy sumę  początkowych wyrazów tego ciągu, dla liczb naturalnych
początkowych wyrazów tego ciągu, dla liczb naturalnych 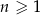 . Wiadomo, że dla pewnego ciągu geometrycznego:
. Wiadomo, że dla pewnego ciągu geometrycznego: 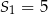 i
i 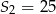 . Wyznacz iloraz i szósty wyraz tego ciągu.
. Wyznacz iloraz i szósty wyraz tego ciągu.
Wyznacz  tak, aby ciąg
tak, aby ciąg 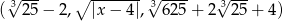 był ciągiem geometrycznym.
był ciągiem geometrycznym.
Funkcja 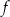 jest określona wzorem
jest określona wzorem 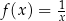 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 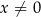 . Oblicz wartość
. Oblicz wartość 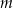 , dla której liczby
, dla której liczby 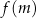 ,
, 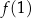 ,
, 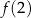 są – odpowiednio – pierwszym, drugim i trzecim wyrazem ciągu geometrycznego.
są – odpowiednio – pierwszym, drugim i trzecim wyrazem ciągu geometrycznego.
Trzy liczby tworzą ciąg arytmetyczny. Jeśli do pierwszej z nich dodamy 5, do drugiej 3, a do trzeciej 4, to otrzymamy rosnący ciąg geometryczny, w którym trzeci wyraz jest cztery razy większy od pierwszego. Znajdź te liczby.
Dla jakich wartości parametru 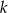 równanie
równanie 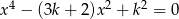 ma co najmniej trzy różne pierwiastki, które są kolejnymi wyrazami ciągu arytmetycznego?
ma co najmniej trzy różne pierwiastki, które są kolejnymi wyrazami ciągu arytmetycznego?

