Wykaż, że liczby 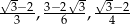 są kolejnymi wyrazami ciągu geometrycznego.
są kolejnymi wyrazami ciągu geometrycznego.
/Szkoła średnia/Ciągi
Dane są dwa ciągi rosnące: arytmetyczny 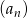 i geometryczny
i geometryczny 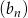 . Pierwsze wyrazy obu ciągów są równe 2, trzecie ich wyrazy są takie same, a jedenasty wyraz ciągu arytmetycznego jest równy piątemu wyrazowi ciągu geometrycznego. Wyznacz te ciągi zapisując wzory na wyrazy ogólne.
. Pierwsze wyrazy obu ciągów są równe 2, trzecie ich wyrazy są takie same, a jedenasty wyraz ciągu arytmetycznego jest równy piątemu wyrazowi ciągu geometrycznego. Wyznacz te ciągi zapisując wzory na wyrazy ogólne.
Dany jest ciąg 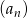 określony dla każdej liczby całkowitej
określony dla każdej liczby całkowitej 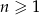 , w którym dla każdej liczby
, w którym dla każdej liczby 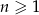 prawdziwe są równości
prawdziwe są równości
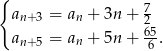
Wykaż, że ciąg 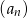 jest ciągiem rosnącym.
jest ciągiem rosnącym.
Pierwszy wyraz ciągu arytmetycznego 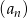 jest równy
jest równy 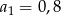 , a jego różnica jest równa
, a jego różnica jest równa 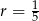 . Oblicz
. Oblicz 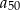 oraz sumę 50 początkowych wyrazów ciągu
oraz sumę 50 początkowych wyrazów ciągu 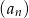 .
.
Oblicz granicę 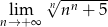 .
.
Oblicz 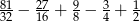 . Wynik podaj w postaci ułamka nieskracalnego.
. Wynik podaj w postaci ułamka nieskracalnego.
W trójkącie dwa boki mają długość 3 cm i 4 cm. Długość trzeciego boku jest większa od długości dwóch pozostałych boków. Długości wysokości w tym trójkącie są trzema kolejnymi wyrazami ciągu arytmetycznego. Oblicz pole tego trójkąta oraz długości promieni okręgów: wpisanego w ten trójkąt i opisanego na tym trójkącie.
Ciąg 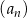 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 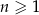 wzorem
wzorem
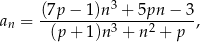
gdzie 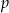 jest liczbą rzeczywistą dodatnią. Oblicz wartość
jest liczbą rzeczywistą dodatnią. Oblicz wartość 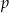 , dla której granica ciągu
, dla której granica ciągu 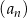 jest równa
jest równa 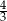 .
.
Ciąg 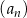 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 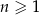 wzorem
wzorem
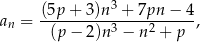
gdzie 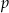 jest liczbą rzeczywistą. Oblicz wartość
jest liczbą rzeczywistą. Oblicz wartość 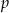 , dla której granica ciągu
, dla której granica ciągu 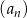 jest równa
jest równa  .
.
W ciągu geometrycznym 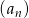 , określonym dla
, określonym dla 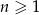 , dane są: wyraz
, dane są: wyraz 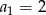 i suma trzech początkowych wyrazów tego ciągu
i suma trzech początkowych wyrazów tego ciągu 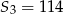 . Wiadomo ponadto, że
. Wiadomo ponadto, że 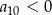 . Oblicz iloraz
. Oblicz iloraz
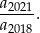
Ciąg 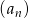 określony jest rekurencyjnie:
określony jest rekurencyjnie: 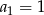 ,
, 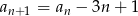 dla
dla 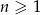 .
.
- Oblicz 4 wyraz ciągu
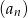 .
. - Zbadaj monotoniczność ciągu
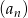 .
.
Dany jest ciąg 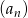 określony dla każdej liczby całkowitej
określony dla każdej liczby całkowitej 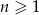 , w którym
, w którym 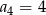 oraz dla każdej liczby
oraz dla każdej liczby 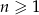 prawdziwa jest równość
prawdziwa jest równość 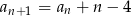 . Oblicz pierwszy wyraz ciągu
. Oblicz pierwszy wyraz ciągu 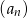 i ustal, czy ciąg ten jest malejący.
i ustal, czy ciąg ten jest malejący.
Ciąg 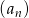 określony jest rekurencyjnie:
określony jest rekurencyjnie: 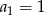 ,
, 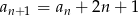 dla
dla 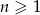 .
.
- Oblicz 4 wyraz ciągu
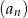 .
. - Zbadaj monotoniczność ciągu
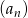 .
.
Dany jest ciąg 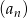 określony dla każdej liczby całkowitej
określony dla każdej liczby całkowitej 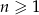 , w którym
, w którym 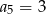 oraz dla każdej liczby
oraz dla każdej liczby 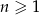 prawdziwa jest równość
prawdziwa jest równość 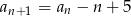 . Oblicz pierwszy wyraz ciągu
. Oblicz pierwszy wyraz ciągu 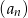 i ustal, czy ciąg ten jest rosnący.
i ustal, czy ciąg ten jest rosnący.
O trapezie 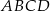 wiadomo, że można w niego wpisać okrąg, a ponadto długości jego boków
wiadomo, że można w niego wpisać okrąg, a ponadto długości jego boków 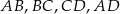 – w podanej kolejności – tworzą ciąg geometryczny. Uzasadnij, że trapez
– w podanej kolejności – tworzą ciąg geometryczny. Uzasadnij, że trapez 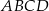 jest rombem.
jest rombem.
Sześcian największej z czterech różnych liczb całkowitych, tworzących rosnący ciąg arytmetyczny o wyrazach dodatnich, jest równy sumie sześcianów pozostałych liczb. Wykaż, że iloczyn dwóch z tych liczb jest o 60% większy od iloczynu dwóch pozostałych.
Wyrazy 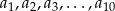 pewnego nieskończonego ciągu
pewnego nieskończonego ciągu 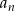 spełniają warunki
spełniają warunki 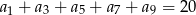 ,
, 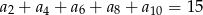 . Wiedząc, że nieskończony ciąg
. Wiedząc, że nieskończony ciąg 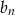 określony wzorem
określony wzorem 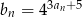 jest ciągiem geometrycznym, oblicz sumę wszystkich wyrazów ciągu
jest ciągiem geometrycznym, oblicz sumę wszystkich wyrazów ciągu 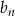 .
.
Wymiary prostopadłościanu o objętości 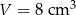 i polu powierzchni całkowitej
i polu powierzchni całkowitej 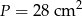 tworzą ciąg geometryczny. Wyznacz długości krawędzi bryły.
tworzą ciąg geometryczny. Wyznacz długości krawędzi bryły.
Długości trzech krawędzi prostopadłościanu tworzą ciąg geometryczny. Objętość bryły jest równa 27, a suma długości jej krawędzi jest równa 52. Znajdź długość najkrótszej krawędzi prostopadłościanu.
Dany jest ciąg 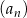 określony wzorem
określony wzorem 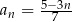 dla każdej liczby naturalnej
dla każdej liczby naturalnej 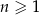 . Trójwyrazowy ciąg
. Trójwyrazowy ciąg 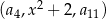 , gdzie
, gdzie  jest liczbą rzeczywistą, jest geometryczny. Oblicz
jest liczbą rzeczywistą, jest geometryczny. Oblicz  oraz iloraz tego ciągu geometrycznego.
oraz iloraz tego ciągu geometrycznego.
Dany jest ciąg 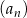 określony wzorem
określony wzorem 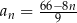 dla każdej liczby naturalnej
dla każdej liczby naturalnej 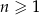 . Trójwyrazowy ciąg
. Trójwyrazowy ciąg 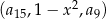 , gdzie
, gdzie  jest dodatnią liczbą rzeczywistą, jest geometryczny. Oblicz
jest dodatnią liczbą rzeczywistą, jest geometryczny. Oblicz  oraz iloraz tego ciągu geometrycznego.
oraz iloraz tego ciągu geometrycznego.
Ile liczb trzeba wstawić między liczby 62 i 440, aby otrzymać ciąg arytmetyczny, którego suma jest równa 2008? Wyznacz różnicę tego ciągu.
Ile liczb trzeba wstawić między liczby 16 i 250, aby otrzymać ciąg arytmetyczny, którego suma jest równa 1995? Wyznacz różnicę tego ciągu.
Długości boków trapezu prostokątnego tworzą ciąg geometryczny. Ramię, które jest najkrótszym bokiem trapezu ma długość 1. Krótsza podstawa trapezu jest krótsza od drugiego z ramion. Oblicz długość dłuższej podstawy.
Podaj wzór na  -ty wyraz ciągu
-ty wyraz ciągu 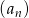 , jeżeli
, jeżeli 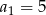 i
i 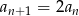 dla
dla 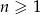 .
.
Niech 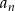 , dla
, dla 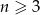 będzie liczbą krawędzi graniastosłupa prostego o podstawie będącej
będzie liczbą krawędzi graniastosłupa prostego o podstawie będącej  -kątem foremnym.
-kątem foremnym.
- Wyznacz wzór ciągu
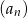 .
. - Sprawdź czy ciąg
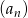 jest ciągiem arytmetycznym.
jest ciągiem arytmetycznym. - Uzasadnij, że żaden wyraz tego ciągu nie jest równy 2009.
Długości boków trójkąta prostokątnego tworzą ciąg arytmetyczny. Jedna z przyprostokątnych ma długość 6. Jaką długość ma druga przyprostokątna oraz przeciwprostokątna?

