Pierwszy wyraz niemonotonicznego ciągu geometrycznego 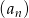 jest równy 48 i jest o 36 większy od wyrazu trzeciego.
jest równy 48 i jest o 36 większy od wyrazu trzeciego.
- Oblicz iloraz ciągu
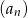 .
. - Oblicz ósmy wyraz ciągu
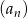 .
. - Suma kilku początkowych wyrazów ciągu
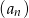 jest równa
jest równa 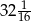 . Oblicz, ile wyrazów zsumowano.
. Oblicz, ile wyrazów zsumowano.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Pierwszy wyraz niemonotonicznego ciągu geometrycznego 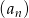 jest równy 48 i jest o 36 większy od wyrazu trzeciego.
jest równy 48 i jest o 36 większy od wyrazu trzeciego.
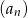 .
. 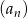 .
. 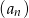 jest równa
jest równa 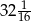 . Oblicz, ile wyrazów zsumowano.
. Oblicz, ile wyrazów zsumowano.Obliczyć granicę 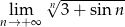 .
.
Dana jest liczba 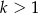 . Wyrazy ciągu
. Wyrazy ciągu 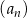 , określonego dla
, określonego dla 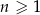 , spełniają warunki
, spełniają warunki
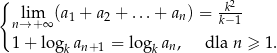
Udowodnij, że
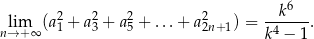
Pierwszy wyraz ciągu arytmetycznego jest równy 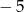 , a suma dwudziestu początkowych wyrazów tego ciągu jest równa 1230. Wyznacz różnicę tego ciągu.
, a suma dwudziestu początkowych wyrazów tego ciągu jest równa 1230. Wyznacz różnicę tego ciągu.
Sprawdź, czy ciąg o wyrazach 2, 6, 18, 36 jest geometryczny.
Długości boków trójkąta 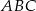 są kolejnymi wyrazami ciągu geometrycznego o ilorazie
są kolejnymi wyrazami ciągu geometrycznego o ilorazie 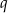 . Wykaż, że miary kątów trójkąta zbudowanego z odcinków o długościach równych długościom wysokości trójkąta
. Wykaż, że miary kątów trójkąta zbudowanego z odcinków o długościach równych długościom wysokości trójkąta 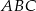 są równe miarom kątów trójkąta
są równe miarom kątów trójkąta 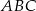 .
.
Długości boków prostokąta i długość jego przekątnej tworzą ciąg arytmetyczny. Oblicz długości jego boków, jeśli obwód prostokąta jest równy 14.
Długości boków prostokąta i długość jego przekątnej tworzą ciąg arytmetyczny. Oblicz długości jego boków, jeśli pole prostokąta jest równe 48.
Oblicz wyrazy 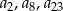 ciągu arytmetycznego jeśli
ciągu arytmetycznego jeśli 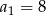 i
i 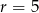 .
.
Dany jest ciąg 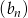 o wyrazie ogólnym
o wyrazie ogólnym 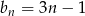 . Ile wyrazów ciągu
. Ile wyrazów ciągu 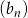 należy do przedziału
należy do przedziału 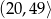 ?
?
Dany jest ciąg określony wzorem 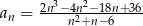 .
.
Wykaż, że jeżeli ciąg 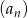 jest ciągiem geometrycznym o wyrazach dodatnich, to ciąg o wyrazie ogólnym
jest ciągiem geometrycznym o wyrazach dodatnich, to ciąg o wyrazie ogólnym 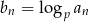 , dla
, dla 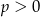 i
i 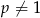 jest ciągiem arytmetycznym.
jest ciągiem arytmetycznym.
Dany jest ciąg geometryczny 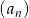 , określony dla
, określony dla 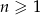 , w którym spełniona jest równość
, w którym spełniona jest równość 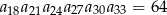 . Oblicz iloczyn
. Oblicz iloczyn 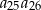 .
.
Pierwszy wyraz malejącego ciągu arytmetycznego 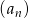 jest równy 3, a iloczyn wyrazów czwartego i piątego równy jest 15. Oblicz różnicę ciągu
jest równy 3, a iloczyn wyrazów czwartego i piątego równy jest 15. Oblicz różnicę ciągu 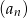 oraz sumę 14 jego początkowych wyrazów.
oraz sumę 14 jego początkowych wyrazów.
Ciąg 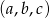 jest geometryczny, a ciągi
jest geometryczny, a ciągi 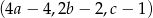 i
i 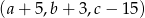 są arytmetyczne. Oblicz
są arytmetyczne. Oblicz 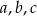 .
.
Trzy liczby o sumie 7 tworzą ciąg geometryczny. Jeżeli do drugiej liczby dodamy pierwszą to ciąg zmieni się w arytmetyczny. Wyznacz pierwszą z tych liczb. Uwzględnij wszystkie możliwości.
Ciąg  jest geometryczny, a ciągi
jest geometryczny, a ciągi 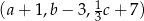 i
i 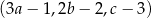 są arytmetyczne. Oblicz
są arytmetyczne. Oblicz 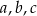 .
.
W ciągu arytmetycznym 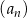 , określonym dla
, określonym dla 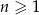 , suma 221 początkowych wyrazów jest równa 1547. Oblicz sumę
, suma 221 początkowych wyrazów jest równa 1547. Oblicz sumę 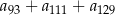 .
.
Dany jest nieskończony ciąg geometryczny 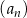 określony dla
określony dla 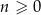 , którego iloraz jest równy
, którego iloraz jest równy 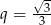 . Suma wszystkich wyrazów tego ciągu jest równa
. Suma wszystkich wyrazów tego ciągu jest równa 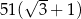 . Oblicz
. Oblicz 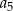 .
.
Ciąg 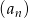 dany jest wzorem
dany jest wzorem 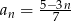 , dla
, dla 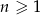 .
.
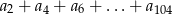 .
. 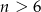 . Dla jakich
. Dla jakich  liczby
liczby 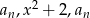 są kolejnymi wyrazami ciągu geometrycznego?
są kolejnymi wyrazami ciągu geometrycznego?Suma  początkowych wyrazów ciągu
początkowych wyrazów ciągu 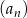 dla każdego
dla każdego 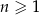 określona jest wzorem
określona jest wzorem 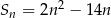 .
.
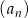 jest ciągiem arytmetycznym.
jest ciągiem arytmetycznym.  początkowych wyrazów ciągu dla każdego
początkowych wyrazów ciągu dla każdego 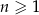 określona jest wzorem
określona jest wzorem 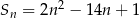 , to ciąg ten nie jest arytmetyczny.
, to ciąg ten nie jest arytmetyczny. 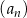 , aby kwadrat środkowego wyrazu był o 48 mniejszy od różnicy kwadratów wyrazów z nim sąsiadujących.
, aby kwadrat środkowego wyrazu był o 48 mniejszy od różnicy kwadratów wyrazów z nim sąsiadujących.Suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 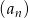 wyraża się wzorem
wyraża się wzorem 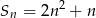 dla
dla 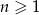 . Oblicz pierwszy wyraz ciągu i jego różnice.
. Oblicz pierwszy wyraz ciągu i jego różnice.
Suma 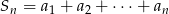 początkowych
początkowych  wyrazów pewnego ciągu arytmetycznego
wyrazów pewnego ciągu arytmetycznego 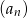 jest określona wzorem
jest określona wzorem 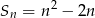 dla
dla 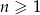 . Wyznacz wzór na
. Wyznacz wzór na  -ty wyraz tego ciągu.
-ty wyraz tego ciągu.
Suma 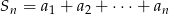 początkowych
początkowych  wyrazów pewnego ciągu arytmetycznego
wyrazów pewnego ciągu arytmetycznego 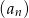 jest określona wzorem
jest określona wzorem 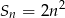 dla
dla 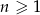 . Wyznacz wzór na
. Wyznacz wzór na  -ty wyraz tego ciągu.
-ty wyraz tego ciągu.
Wykaż, że jeżeli ciąg 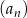 jest ciągiem geometrycznym, to
jest ciągiem geometrycznym, to