Dany jest ciąg geometryczny 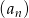 o pierwszym wyrazie równym
o pierwszym wyrazie równym 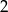 , i ilorazie równym 10. Wykaż, że wszystkie punkty o współrzędnych
, i ilorazie równym 10. Wykaż, że wszystkie punkty o współrzędnych 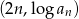 leżą na jednej prostej.
leżą na jednej prostej.
/Szkoła średnia/Ciągi
W nieskończonym ciągu geometrycznym 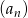 o wyrazach dodatnich każdy wyraz począwszy od trzeciego, jest sumą dwóch poprzednich wyrazów. Oblicz iloraz tego ciągu.
o wyrazach dodatnich każdy wyraz począwszy od trzeciego, jest sumą dwóch poprzednich wyrazów. Oblicz iloraz tego ciągu.
Różnica między pierwszym a siódmym wyrazem ciągu geometrycznego jest równa 63, a różnica między wyrazem pierwszym a czwartym jest równa 72. Oblicz sumę pierwszych 7 wyrazów tego ciągu.
Sinusy kątów ostrych trójkąta prostokątnego oraz liczba 1 tworzą ze sobą ciąg geometryczny. Oblicz sinus najmniejszego kąta tego trójkąta.
Cztery liczby tworzą ciąg geometryczny. Jeżeli od pierwszej z nich odejmiemy 2, od drugiej 3, od trzeciej 9, a od czwartej 25, to otrzymane różnice utworzą ciąg arytmetyczny. Znajdź te liczby.
Ciąg 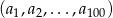 jest ciągiem geometrycznym o ilorazie
jest ciągiem geometrycznym o ilorazie 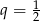 i pierwszym wyrazie równym
i pierwszym wyrazie równym 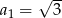 . Oblicz sumę
. Oblicz sumę
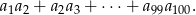
W ciągu geometrycznym 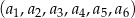 suma wyrazów o numerach nieparzystych jest równa 182, a stosunek sumy wyrazów o numerach nieparzystych do sumy wyrazów o numerach parzystych jest równy
suma wyrazów o numerach nieparzystych jest równa 182, a stosunek sumy wyrazów o numerach nieparzystych do sumy wyrazów o numerach parzystych jest równy 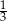 . Wyznacz wszystkie wyrazy tego ciągu.
. Wyznacz wszystkie wyrazy tego ciągu.
Dla jakich wartości  liczby
liczby 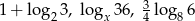 są kolejnymi wyrazami ciągu geometrycznego.
są kolejnymi wyrazami ciągu geometrycznego.
Dany jest nieskończony ciąg geometryczny 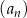 określony dla
określony dla 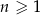 , którego wyrazy są niezerowe i iloraz
, którego wyrazy są niezerowe i iloraz 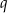 spełnia warunek:
spełnia warunek: 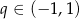 . Suma
. Suma 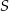 wszystkich wyrazów ciągu
wszystkich wyrazów ciągu 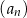 , suma
, suma 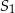 wszystkich wyrazów ciągu
wszystkich wyrazów ciągu 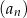 o numerach nieparzystych oraz suma
o numerach nieparzystych oraz suma 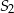 wszystkich wyrazów ciągu
wszystkich wyrazów ciągu 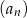 o numerach parzystych są kolejnymi wyrazami ciągu geometrycznego. Oblicz
o numerach parzystych są kolejnymi wyrazami ciągu geometrycznego. Oblicz 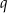 .
.
Dany jest nieskończony ciąg geometryczny 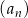 , określony dla każdej liczby naturalnej
, określony dla każdej liczby naturalnej 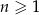 , którego iloraz
, którego iloraz 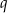 jest równy pierwszemu wyrazowi i spełnia warunek
jest równy pierwszemu wyrazowi i spełnia warunek 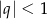 . Stosunek sumy
. Stosunek sumy 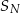 wszystkich wyrazów tego ciągu o numerach nieparzystych do sumy
wszystkich wyrazów tego ciągu o numerach nieparzystych do sumy 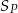 wszystkich wyrazów tego ciągu o numerach parzystych jest równy różnicy tych sum, tj.
wszystkich wyrazów tego ciągu o numerach parzystych jest równy różnicy tych sum, tj. 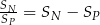 . Oblicz
. Oblicz 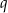 .
.
Suma 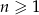 początkowych wyrazów ciągu
początkowych wyrazów ciągu 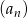 wyraża się wzorem
wyraża się wzorem 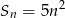 . Oblicz, ile wyrazów tego ciągu jest liczbami trzycyfrowymi.
. Oblicz, ile wyrazów tego ciągu jest liczbami trzycyfrowymi.
Wykaż, że zbiór 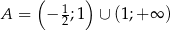 jest zbiorem wartości funkcji
jest zbiorem wartości funkcji
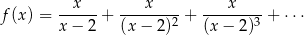
Na płaszczyźnie z prostokątnym układem współrzędnych zilustruj zbiór wszystkich punktów płaszczyzny o współrzędnych 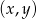 , dla których ciąg:
, dla których ciąg: 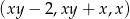 jest rosnącym ciągiem arytmetycznym.
jest rosnącym ciągiem arytmetycznym.
Wykazać, że 1 nie jest wyrazem ciągu 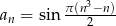 .
.
Liczby  i
i 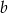 są pierwiastkami równania
są pierwiastkami równania 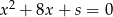 , a liczby
, a liczby  i
i 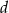 są pierwiastkami równania
są pierwiastkami równania 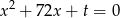 . Ciąg
. Ciąg 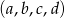 jest malejącym ciągiem geometrycznym. Oblicz
jest malejącym ciągiem geometrycznym. Oblicz  i
i 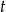 .
.
Dany jest czterowyrazowy ciąg 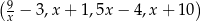 . Oblicz wszystkie wartości
. Oblicz wszystkie wartości  , dla których ten ciąg jest geometryczny.
, dla których ten ciąg jest geometryczny.
Oblicz granicę
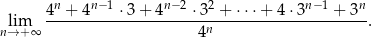
Ciąg 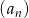 określony jest wzorem
określony jest wzorem 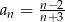 .
.
- Oblicz dziesiąty wyraz ciągu.
- Oblicz, który wyraz ciągu jest równy
 .
.
Trzy liczby są kolejnymi wyrazami ciągu arytmetycznego. Ich suma wynosi 18. Jeśli największą z tych liczb zwiększymy o 8, a pozostałych nie zmienimy, to uzyskamy trzy kolejne wyrazy ciągu geometrycznego. Wyznacz te liczby.
Trzy liczby są kolejnymi wyrazami ciągu arytmetycznego. Ich suma wynosi 27. Jeśli największą z tych liczb zwiększymy o 12, a pozostałych nie zmienimy, to uzyskamy trzy kolejne wyrazy ciągu geometrycznego. Wyznacz te liczby.
Trzy liczby tworzą ciąg geometryczny. Jeżeli drugą z nich zwiększymy o 8, to otrzymamy ciąg arytmetyczny. Jeżeli trzeci wyraz otrzymanego ciągu arytmetycznego zwiększymy o 64 to znów otrzymamy ciąg geometryczny. Wyznacz te liczby.
Trzy liczby są kolejnymi wyrazami ciągu geometrycznego, którego iloraz jest różny od 1. Jeżeli weźmiemy kolejno drugą z nich, pierwszą i trzecią, to otrzymamy trzy kolejne wyrazy ciągu arytmetycznego. Jeżeli pierwszy wyraz tego ciągu arytmetycznego zmniejszymy o 7, drugi pozostawimy bez zmian, a trzeci zwiększymy o 3, to otrzymamy trzy kolejne wyrazy ciągu geometrycznego. Oblicz te liczby.
Dany jest nieskończony ciąg geometryczny 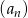 określony dla
określony dla 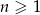 , w którym pierwszy wyraz jest liczbą naturalną, a iloczyn pierwszego i trzeciego wyrazu jest równy 1. Suma wszystkich wyrazów tego ciągu jest liczbą z przedziału
, w którym pierwszy wyraz jest liczbą naturalną, a iloczyn pierwszego i trzeciego wyrazu jest równy 1. Suma wszystkich wyrazów tego ciągu jest liczbą z przedziału 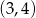 . Oblicz iloraz tego ciągu.
. Oblicz iloraz tego ciągu.

