Ile wyrazów ciągu o wyrazie ogólnym 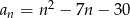 , dla
, dla 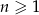 , jest liczbami ujemnymi?
, jest liczbami ujemnymi?
/Szkoła średnia/Ciągi
Ile wyrazów ujemnych ma ciąg 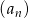 określony wzorem
określony wzorem 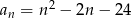 dla
dla 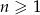 ?
?
Ile wyrazów ujemnych ma ciąg 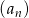 określony wzorem
określony wzorem 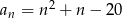 dla
dla 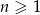 ?
?
Ile wyrazów ciągu o wyrazie ogólnym 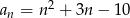 , dla
, dla 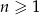 , jest liczbami ujemnymi?
, jest liczbami ujemnymi?
Ciąg 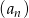 określony jest wzorem
określony jest wzorem 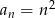 . Wyraź w zależności od
. Wyraź w zależności od  , rożnicę
, rożnicę 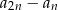 .
.
Iloraz ciągu geometrycznego 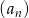 równy jest 3, a suma odwrotności wyrazu pierwszego i drugiego wynosi 18.
równy jest 3, a suma odwrotności wyrazu pierwszego i drugiego wynosi 18.
- Oblicz pierwszy wyraz ciągu
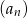 .
. - Podaj wzór na wyraz ogólny ciągu
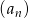 .
.
Suma 2018 początkowych wyrazów ciągu geometrycznego 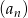 jest równa 1417, a suma odwrotności tych wyrazów jest równa 109. Oblicz iloczyn 2018 początkowych wyrazów ciągu
jest równa 1417, a suma odwrotności tych wyrazów jest równa 109. Oblicz iloczyn 2018 początkowych wyrazów ciągu 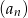 .
.
Liczby 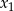 i
i 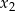 są różnymi miejscami zerowymi funkcji kwadratowej
są różnymi miejscami zerowymi funkcji kwadratowej 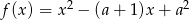 . Dla jakich
. Dla jakich 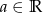 ciąg
ciąg 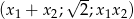 jest geometryczny?
jest geometryczny?
Dany jest ciąg geometryczny 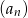 określony wzorem
określony wzorem 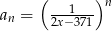 dla
dla 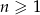 . Wszystkie wyrazy tego ciągu są dodatnie. Wyznacz najmniejszą liczbę całkowitą
. Wszystkie wyrazy tego ciągu są dodatnie. Wyznacz najmniejszą liczbę całkowitą  , dla której nieskończony szereg
, dla której nieskończony szereg 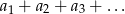 jest zbieżny.
jest zbieżny.
Dany jest ciąg geometryczny 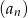 określony wzorem
określony wzorem 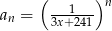 dla
dla 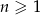 , którego niektóre wyrazy są ujemne. Wyznacz największą liczbę całkowitą
, którego niektóre wyrazy są ujemne. Wyznacz największą liczbę całkowitą  , dla której nieskończony szereg
, dla której nieskończony szereg 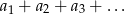 jest zbieżny.
jest zbieżny.
Suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 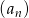 wyraża się wzorem
wyraża się wzorem 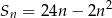 , gdzie
, gdzie 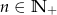 . Oblicz
. Oblicz  wiedząc, że liczby:
wiedząc, że liczby: 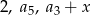 w podanej kolejności tworzą ciąg geometryczny.
w podanej kolejności tworzą ciąg geometryczny.
Suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 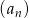 wyraża się wzorem
wyraża się wzorem 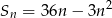 , gdzie
, gdzie 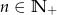 . Oblicz
. Oblicz  wiedząc, że liczby:
wiedząc, że liczby: 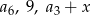 w podanej kolejności tworzą ciąg geometryczny.
w podanej kolejności tworzą ciąg geometryczny.
Rozważamy nieskończone ciągi geometryczne o ilorazie 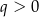 , w których kwadrat drugiego wyrazu jest dodatni i równy sumie wyrazów: drugiego, trzeciego i czwartego. Wyznacz pierwszy wyraz i iloraz tego spośród rozpatrywanych ciągów, którego suma wszystkich wyrazów jest najmniejsza. Oblicz tę sumę.
, w których kwadrat drugiego wyrazu jest dodatni i równy sumie wyrazów: drugiego, trzeciego i czwartego. Wyznacz pierwszy wyraz i iloraz tego spośród rozpatrywanych ciągów, którego suma wszystkich wyrazów jest najmniejsza. Oblicz tę sumę.
Na jednym z ramion kąta ostrego o wierzchołku 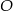 i mierze
i mierze  wybrano punkty
wybrano punkty 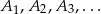 , a na drugim ramieniu punkty
, a na drugim ramieniu punkty 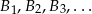 w ten sposób, że
w ten sposób, że 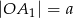 ,
, 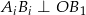 oraz
oraz 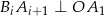 dla wszystkich
dla wszystkich 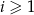 .
.
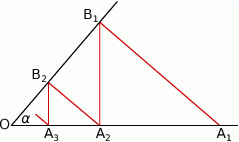
Wykaż, że długość nieskończonej łamanej 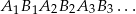 jest równa
jest równa 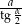 .
.
Między liczby 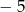 i 49 wstaw dwie liczby tak, aby trzy pierwsze tworzyły ciąg arytmetyczny, a trzy ostatnie ciąg geometryczny.
i 49 wstaw dwie liczby tak, aby trzy pierwsze tworzyły ciąg arytmetyczny, a trzy ostatnie ciąg geometryczny.
Między liczby 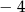 i 36 wstaw dwie liczby tak, aby trzy pierwsze tworzyły ciąg arytmetyczny, a trzy ostatnie ciąg geometryczny.
i 36 wstaw dwie liczby tak, aby trzy pierwsze tworzyły ciąg arytmetyczny, a trzy ostatnie ciąg geometryczny.
Czterowyrazowy ciąg 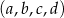 jest rosnący i arytmetyczny. Suma kwadratów trzech najmniejszych wyrazów tego ciągu jest pięciokrotnie większa od kwadratu czwartego wyrazu. Ponadto ciąg
jest rosnący i arytmetyczny. Suma kwadratów trzech najmniejszych wyrazów tego ciągu jest pięciokrotnie większa od kwadratu czwartego wyrazu. Ponadto ciąg 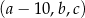 jest geometryczny. Oblicz wyrazy ciągu
jest geometryczny. Oblicz wyrazy ciągu 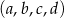 .
.
Czterowyrazowy ciąg 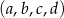 jest rosnący i arytmetyczny. Kwadrat największego wyrazu tego ciągu jest równy podwojonej sumie kwadratów pozostałych wyrazów tego ciągu. Ponadto ciąg
jest rosnący i arytmetyczny. Kwadrat największego wyrazu tego ciągu jest równy podwojonej sumie kwadratów pozostałych wyrazów tego ciągu. Ponadto ciąg 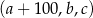 jest geometryczny. Oblicz wyrazy ciągu
jest geometryczny. Oblicz wyrazy ciągu 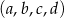 .
.
Czterowyrazowy ciąg 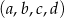 jest rosnący i arytmetyczny. Kwadrat największego wyrazu tego ciągu jest równy podwojonej sumie kwadratów pozostałych wyrazów tego ciągu. Ponadto ciąg
jest rosnący i arytmetyczny. Kwadrat największego wyrazu tego ciągu jest równy podwojonej sumie kwadratów pozostałych wyrazów tego ciągu. Ponadto ciąg 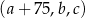 jest geometryczny. Oblicz wyrazy ciągu
jest geometryczny. Oblicz wyrazy ciągu 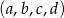 .
.
W trójkąt równoboczny 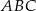 o boku długości 1 wpisano koło. Prowadzimy proste równoległe do boków trójkąta
o boku długości 1 wpisano koło. Prowadzimy proste równoległe do boków trójkąta 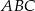 i styczne do koła wpisanego. Proste te odcinają od trójkąta
i styczne do koła wpisanego. Proste te odcinają od trójkąta 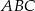 trzy trójkąty równoboczne. W każdy z nich wpisujemy koło i postępujemy analogicznie jak z kołem wpisanym w trójkąt
trzy trójkąty równoboczne. W każdy z nich wpisujemy koło i postępujemy analogicznie jak z kołem wpisanym w trójkąt 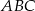 . Czynność tę powtórzono nieskończenie wiele razy. Oblicz sumę pól wszystkich otrzymanych w ten sposób kół.
. Czynność tę powtórzono nieskończenie wiele razy. Oblicz sumę pól wszystkich otrzymanych w ten sposób kół.
Nieskończony ciąg liczbowy 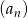 dla
dla 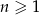 jest określony wzorem
jest określony wzorem
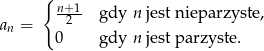
- Uzupełnij tabelkę:

1 2 3 4 5 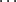
2005 2006 2007 2008 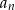
1 0 … - Oblicz
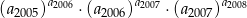 .
. - Oblicz sumę 2008 początkowych wyrazów ciągu
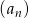 .
.
Trzy liczby tworzą ciąg arytmetyczny o 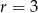 . Jeżeli pierwszą powiększymy o 8 drugą o 6 a trzecią pozostawimy bez zmian to otrzymamy trzy kolejne wyrazy ciągu geometrycznego. Znajdź te liczby.
. Jeżeli pierwszą powiększymy o 8 drugą o 6 a trzecią pozostawimy bez zmian to otrzymamy trzy kolejne wyrazy ciągu geometrycznego. Znajdź te liczby.
Trzy liczby tworzą ciąg arytmetyczny o 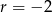 . Jeżeli pierwszą powiększymy o 3 drugą o 1 a trzecią pozostawimy bez zmian to otrzymamy trzy kolejne wyrazy ciągu geometrycznego. Znajdź te liczby.
. Jeżeli pierwszą powiększymy o 3 drugą o 1 a trzecią pozostawimy bez zmian to otrzymamy trzy kolejne wyrazy ciągu geometrycznego. Znajdź te liczby.
Wyrazy ciągu geometrycznego 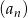 , określonego dla
, określonego dla 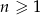 , spełniają układ równań
, spełniają układ równań
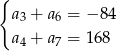
Wyznacz liczbę  początkowych wyrazów tego ciągu, których suma
początkowych wyrazów tego ciągu, których suma 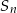 jest równa 32769.
jest równa 32769.
Wyrazy ciągu geometrycznego 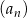 , określonego dla
, określonego dla 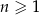 , spełniają układ równań
, spełniają układ równań
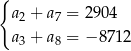
Wyznacz liczbę  początkowych wyrazów tego ciągu, których suma
początkowych wyrazów tego ciągu, których suma 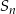 jest równa 177148.
jest równa 177148.
Różnica między drugim wyrazem ciągu geometrycznego a pierwszym wyrazem tego ciągu wynosi -6, a różnica między czwartym a pierwszym wyrazem tego ciągu jest równa -18. Oblicz trzeci wyraz tego ciągu.
Dane jest koło 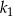 o promieniu
o promieniu  . W tym kole narysowano koło
. W tym kole narysowano koło 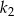 styczne wewnętrznie, którego pole jest równe połowie pola koła
styczne wewnętrznie, którego pole jest równe połowie pola koła 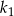 . W kole
. W kole 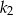 narysowano koło
narysowano koło 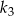 styczne wewnętrznie, którego pole jest równe połowie pola koła
styczne wewnętrznie, którego pole jest równe połowie pola koła 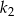 . Czynność tę powtórzono nieskończenie wiele razy. Oblicz sumę obwodów wszystkich narysowanych kół.
. Czynność tę powtórzono nieskończenie wiele razy. Oblicz sumę obwodów wszystkich narysowanych kół.
Liczby 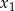 i
i 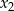 są różnymi od zera rozwiązaniami równania
są różnymi od zera rozwiązaniami równania 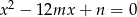 . Liczby
. Liczby 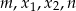 są kolejnymi wyrazami pewnego ciągu geometrycznego. Wyznacz
są kolejnymi wyrazami pewnego ciągu geometrycznego. Wyznacz 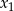 i
i 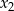 .
.
Trzy liczby, których suma jest równa 93, tworzą ciąg geometryczny. Te same liczby stanowią pierwszy, drugi oraz siódmy wyraz ciągu arytmetycznego. Wyznacz te liczby.
Trzy liczby tworzą rosnący ciąg geometryczny. Suma tych liczb jest równa 28. Liczby te są jednocześnie 1, 2 i 4 wyrazem ciągu arytmetycznego. Jakie to liczby?
Liczby 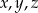 w podanej kolejności, tworzą ciąg geometryczny. Suma tych liczb wynosi 13. Te same liczby, w podanej kolejności, są odpowiednio pierwszym, drugim i piątym wyrazem ciągu arytmetycznego. Wyznacz,
w podanej kolejności, tworzą ciąg geometryczny. Suma tych liczb wynosi 13. Te same liczby, w podanej kolejności, są odpowiednio pierwszym, drugim i piątym wyrazem ciągu arytmetycznego. Wyznacz, 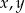 oraz
oraz  .
.
Trzywyrazowy ciąg 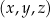 jest geometryczny i rosnący. Suma wyrazów tego ciągu jest równa 105. Liczby
jest geometryczny i rosnący. Suma wyrazów tego ciągu jest równa 105. Liczby 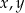 oraz
oraz  są – odpowiednio – pierwszym, drugim oraz szóstym wyrazem ciągu arytmetycznego
są – odpowiednio – pierwszym, drugim oraz szóstym wyrazem ciągu arytmetycznego 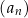 , określonego dla każdej liczby naturalnej
, określonego dla każdej liczby naturalnej 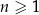 . Oblicz
. Oblicz 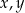 oraz
oraz  .
.
W trzywyrazowym ciągu geometrycznym 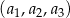 spełniona jest równość
spełniona jest równość 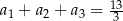 . Wyrazy
. Wyrazy 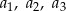 są – odpowiednio – dziewiątym, trzecim i pierwszym wyrazem rosnącego ciągu arytmetycznego. Oblicz
są – odpowiednio – dziewiątym, trzecim i pierwszym wyrazem rosnącego ciągu arytmetycznego. Oblicz 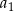 .
.
W trzywyrazowym ciągu geometrycznym 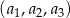 spełniona jest równość
spełniona jest równość 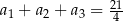 . Wyrazy
. Wyrazy 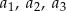 są – odpowiednio – czwartym, drugim i pierwszym wyrazem rosnącego ciągu arytmetycznego. Oblicz
są – odpowiednio – czwartym, drugim i pierwszym wyrazem rosnącego ciągu arytmetycznego. Oblicz  .
.
Trzy liczby, których suma jest równa 105, są kolejnymi wyrazami rosnącego ciągu geometrycznego. Pierwsza z tych liczb jest jednocześnie pierwszym, druga szóstym, a trzecia dwudziestym szóstym wyrazem pewnego ciągu arytmetycznego. Oblicz te liczby.
W ciągu arytmetycznym o nieparzystej liczbie wyrazów suma wyrazów stojących na miejscach nieparzystych równa się 44, a suma pozostałych wynosi 33. Znajdź wyraz środkowy i liczbę wyrazów tego ciągu.

