Ciąg 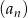 jest arytmetyczny oraz
jest arytmetyczny oraz 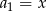 i
i 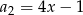 . Wiedząc, że
. Wiedząc, że 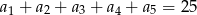 oblicz
oblicz  oraz sumę
oraz sumę 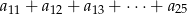 .
.
/Szkoła średnia/Ciągi
Oblicz granicę 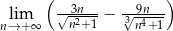 .
.
Suma trzech początkowych wyrazów nieskończonego ciągu geometrycznego 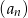 wynosi 6, a suma
wynosi 6, a suma 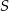 wszystkich wyrazów tego ciągu jest równa
wszystkich wyrazów tego ciągu jest równa 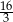 . Oblicz iloraz ciągu
. Oblicz iloraz ciągu 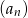 .
.
Suma trzech początkowych wyrazów nieskończonego ciągu geometrycznego 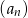 wynosi 18, a suma
wynosi 18, a suma 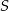 wszystkich wyrazów tego ciągu jest równa 16. Oblicz pierwszy wyraz
wszystkich wyrazów tego ciągu jest równa 16. Oblicz pierwszy wyraz 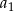 tego ciągu.
tego ciągu.
Suma trzech początkowych wyrazów nieskończonego ciągu geometrycznego 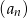 wynosi 14, a suma
wynosi 14, a suma 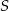 wszystkich wyrazów tego ciągu jest równa
wszystkich wyrazów tego ciągu jest równa 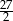 . Oblicz iloraz ciągu
. Oblicz iloraz ciągu 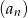 .
.
Suma trzech początkowych wyrazów nieskończonego ciągu geometrycznego 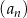 wynosi 18, a suma
wynosi 18, a suma 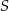 wszystkich wyrazów tego ciągu jest równa 16. Oblicz iloraz tego ciągu.
wszystkich wyrazów tego ciągu jest równa 16. Oblicz iloraz tego ciągu.
Suma trzech początkowych wyrazów nieskończonego ciągu geometrycznego 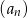 wynosi
wynosi 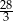 , a suma
, a suma 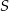 wszystkich wyrazów tego ciągu jest równa 9. Oblicz pierwszy wyraz
wszystkich wyrazów tego ciągu jest równa 9. Oblicz pierwszy wyraz 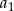 tego ciągu.
tego ciągu.
Suma trzech początkowych wyrazów nieskończonego ciągu geometrycznego 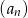 wynosi 14, a suma
wynosi 14, a suma 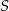 wszystkich wyrazów tego ciągu jest równa
wszystkich wyrazów tego ciągu jest równa 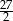 . Oblicz pierwszy wyraz
. Oblicz pierwszy wyraz 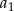 tego ciągu.
tego ciągu.
Suma trzech początkowych wyrazów nieskończonego ciągu geometrycznego 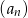 wynosi 6, a suma
wynosi 6, a suma 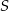 wszystkich wyrazów tego ciągu jest równa
wszystkich wyrazów tego ciągu jest równa 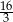 . Oblicz pierwszy wyraz
. Oblicz pierwszy wyraz 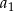 tego ciągu.
tego ciągu.
Suma trzech początkowych wyrazów nieskończonego ciągu geometrycznego 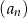 wynosi
wynosi 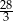 , a suma
, a suma 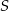 wszystkich wyrazów tego ciągu jest równa 9. Oblicz iloraz ciągu
wszystkich wyrazów tego ciągu jest równa 9. Oblicz iloraz ciągu 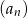 .
.
Uzasadnij, że ciąg określony wzorem 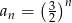 jest ciągiem geometrycznym. Wyznacz iloraz tego ciągu.
jest ciągiem geometrycznym. Wyznacz iloraz tego ciągu.
Liczby 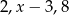 są w podanej kolejności pierwszym, drugim i czwartym wyrazem ciągu arytmetycznego. Oblicz
są w podanej kolejności pierwszym, drugim i czwartym wyrazem ciągu arytmetycznego. Oblicz  .
.
Liczby 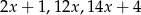 są w podanej kolejności pierwszym, drugim i czwartym wyrazem ciągu arytmetycznego. Oblicz
są w podanej kolejności pierwszym, drugim i czwartym wyrazem ciągu arytmetycznego. Oblicz  .
.
Obwód trapezu równoramiennego wynosi 116. Oblicz pole tego trapezu, jeśli długości ramienia i podstaw trapezu są (w podanej kolejności) trzema kolejnymi wyrazami ciągu arytmetycznego oraz długość odcinka łączącego środki ramion trapezu wynosi 41.
Ciąg 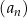 jest określony wzorem
jest określony wzorem
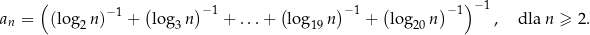
Oblicz sumę 19 początkowych wyrazów ciągu 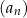 .
.
Monotoniczny ciąg geometryczny 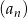 jest zdefiniowany przez warunki
jest zdefiniowany przez warunki
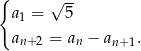
Oblicz sumę wszystkich wyrazów ciągu 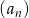 .
.
Liczby 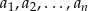 są dodatnie i w podanej kolejności tworzą ciąg geometryczny. Uzasadnij, że prawdziwa jest równość
są dodatnie i w podanej kolejności tworzą ciąg geometryczny. Uzasadnij, że prawdziwa jest równość 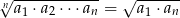 .
.
Oblicz iloczyn pierwszych 99 wyrazów ciągu geometrycznego 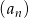 , w którym
, w którym 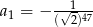 oraz
oraz 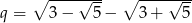 . Czy iloczyn ten jest liczbą wymierną?
. Czy iloczyn ten jest liczbą wymierną?
Ciąg arytmetyczny 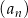 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 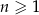 . Różnicą tego ciągu jest liczba
. Różnicą tego ciągu jest liczba 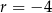 , a średnia arytmetyczna początkowych sześciu wyrazów tego ciągu:
, a średnia arytmetyczna początkowych sześciu wyrazów tego ciągu: 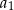 ,
, 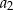 ,
, 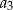 ,
, 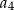 ,
, 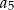 ,
, 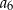 , jest równa 16.
, jest równa 16.
- Oblicz pierwszy wyraz tego ciągu.
- Oblicz liczbę
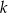 , dla której
, dla której 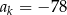 .
.
Ciąg arytmetyczny 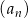 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 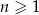 . Różnicą tego ciągu jest liczba
. Różnicą tego ciągu jest liczba 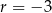 , a średnia arytmetyczna początkowych siedmiu wyrazów tego ciągu:
, a średnia arytmetyczna początkowych siedmiu wyrazów tego ciągu: 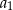 ,
, 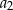 ,
, 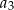 ,
, 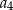 ,
, 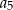 ,
, 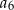 ,
, 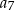 , jest równa
, jest równa 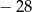 .
.
- Oblicz pierwszy wyraz tego ciągu.
- Wyznacz najmniejszą liczbę
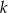 , dla której
, dla której 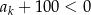 .
.
Wyznacz pierwsze trzy wyrazy ciągu geometrycznego wiedząc, że ich suma jest równa 10,5 oraz suma ich kwadratów jest równa 47,25.
Niech 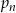 , dla liczby całkowitej
, dla liczby całkowitej 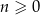 , oznacza sumę odwrotności pierwiastków równania
, oznacza sumę odwrotności pierwiastków równania
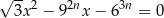
z niewiadomą  . Oblicz sumę wszystkich wyrazów ciągu
. Oblicz sumę wszystkich wyrazów ciągu 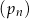 .
.
Ciąg 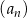 jest określony dla
jest określony dla 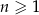 i spełnia warunki
i spełnia warunki
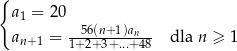
Oblicz granicę
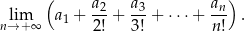
Oblicz granicę 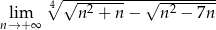 .
.
Udowodnij, że liczba 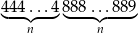 jest kwadratem liczby naturalnej.
jest kwadratem liczby naturalnej.
Ciąg geometryczny 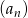 jest określony wzorem
jest określony wzorem 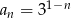 dla
dla 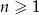 .
.
- Oblicz iloraz tego ciągu.
- Oblicz
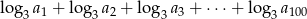 czyli sumę logarytmów, o podstawie 3, stu początkowych, kolejnych wyrazów tego ciągu.
czyli sumę logarytmów, o podstawie 3, stu początkowych, kolejnych wyrazów tego ciągu.
W trójkącie prostokątnym długości wysokości i środkowej poprowadzonej z wierzchołka kąta prostego oraz długość przeciwprostokątnej tworzą ciąg geometryczny, w którym iloczyn wyrazów jest równy 8. Oblicz promień okręgu wpisanego w ten trójkąt.
Znajdź wartość parametru 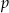 , dla której granica ciągu
, dla której granica ciągu 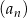 określonego wzorem
określonego wzorem
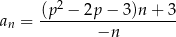
jest równa 4. Zbadaj monotoniczność ciągu 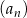 dla znalezionej wartości
dla znalezionej wartości 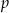 .
.
Naszkicuj wykres ciągu o podanych wyrazach początkowych: 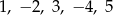 . Odgadnij wzór ogólny tego ciągu.
. Odgadnij wzór ogólny tego ciągu.
Naszkicuj wykres ciągu o podanych wyrazach początkowych: 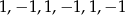 . Odgadnij wzór ogólny tego ciągu.
. Odgadnij wzór ogólny tego ciągu.
Naszkicuj wykres ciągu o podanych wyrazach początkowych: 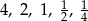 . Odgadnij wzór ogólny tego ciągu.
. Odgadnij wzór ogólny tego ciągu.
Naszkicuj wykres ciągu o podanych wyrazach początkowych: 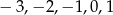 . Odgadnij wzór ogólny tego ciągu.
. Odgadnij wzór ogólny tego ciągu.

