Ciąg 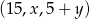 jest arytmetyczny, natomiast ciąg
jest arytmetyczny, natomiast ciąg 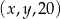 jest geometryczny. Oblicz
jest geometryczny. Oblicz  oraz
oraz 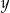 i podaj ten ciąg geometryczny.
i podaj ten ciąg geometryczny.
/Szkoła średnia/Ciągi
Ciąg 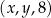 jest malejącym ciągiem geometrycznym. Jeżeli pierwszy wyraz tego ciągu zmniejszymy o 2, to otrzymamy trzywyrazowy ciąg arytmetyczny. Wyznacz
jest malejącym ciągiem geometrycznym. Jeżeli pierwszy wyraz tego ciągu zmniejszymy o 2, to otrzymamy trzywyrazowy ciąg arytmetyczny. Wyznacz  i
i 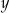 .
.
Liczby dodatnie 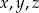 są wyrazami ciągu geometrycznego o numerach równych odpowiednio
są wyrazami ciągu geometrycznego o numerach równych odpowiednio 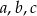 , a liczby
, a liczby 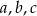 są kolejnymi wyrazami ciągu geometrycznego. Wykaż, że
są kolejnymi wyrazami ciągu geometrycznego. Wykaż, że
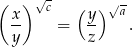
Dany jest ciąg arytmetyczny 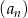 określony dla każdej liczby naturalnej
określony dla każdej liczby naturalnej 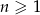 , w którym suma pierwszych 50 wyrazów jest równa 9 900, a suma wyrazów o numerach od 41 do 70 (włącznie) jest równa 540. Oblicz sumę wszystkich dodatnich wyrazów tego ciągu.
, w którym suma pierwszych 50 wyrazów jest równa 9 900, a suma wyrazów o numerach od 41 do 70 (włącznie) jest równa 540. Oblicz sumę wszystkich dodatnich wyrazów tego ciągu.
Dany jest ciąg arytmetyczny 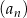 określony dla każdej liczby naturalnej
określony dla każdej liczby naturalnej 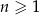 , w którym suma pierwszych 60 wyrazów jest równa 108 750, a suma wyrazów o numerach od 31 do 50 (włącznie) jest równa 34 850. Wyznacz największy wyraz tego ciągu.
, w którym suma pierwszych 60 wyrazów jest równa 108 750, a suma wyrazów o numerach od 31 do 50 (włącznie) jest równa 34 850. Wyznacz największy wyraz tego ciągu.
W siedmiowyrazowym ciągu arytmetycznym środkowy wyraz jest równy 0. Udowodnij, że suma wyrazów tego ciągu jest równa 0.
Iloczyn wszystkich wyrazów ciągu danego wzorem
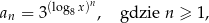
jest równy 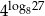 . Oblicz
. Oblicz  .
.
Ciąg 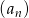 , dla
, dla 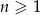 jest ciągiem geometrycznym o ilorazie
jest ciągiem geometrycznym o ilorazie 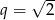 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia
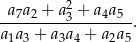
Dany jest ciąg 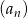 , w którym suma
, w którym suma  początkowych wyrazów wyraża się wzorem
początkowych wyrazów wyraża się wzorem 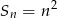 ,
, 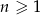 . Wyznacz wzór ogólny ciągu. Czy jest to ciąg arytmetyczny?
. Wyznacz wzór ogólny ciągu. Czy jest to ciąg arytmetyczny?
Dany jest ciąg 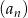 , w którym suma
, w którym suma  początkowych wyrazów wyraża się wzorem
początkowych wyrazów wyraża się wzorem 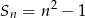 ,
, 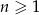 . Wyznacz wzór ogólny ciągu. Czy jest to ciąg arytmetyczny?
. Wyznacz wzór ogólny ciągu. Czy jest to ciąg arytmetyczny?
Dany jest skończony ciąg, w którym pierwszy wyraz jest równy 444, a ostatni jest równy 653. Każdy wyraz tego ciągu, począwszy od drugiego, jest o 11 większy od wyrazu bezpośrednio go poprzedzającego. Oblicz sumę wszystkich wyrazów tego ciągu.
Długości boków trójkąta prostokątnego o obwodzie 30 cm są pierwszym, piętnastym i siedemnastym wyrazem rosnącego ciągu arytmetycznego. Oblicz pole tego trójkąta.
Trójwyrazowy ciąg 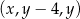 jest arytmetyczny. Suma wszystkich wyrazów tego ciągu jest równa 6. Oblicz wszystkie wyrazy tego ciągu.
jest arytmetyczny. Suma wszystkich wyrazów tego ciągu jest równa 6. Oblicz wszystkie wyrazy tego ciągu.
Wykaż, że suma szeregu geometrycznego zbieżnego jest ujemna wtedy i tylko wtedy, gdy jego pierwszy wyraz jest ujemny.
W skończonym ciągu arytmetycznym 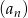 pierwszy wyraz
pierwszy wyraz 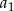 jest równy 7 oraz ostatni wyraz
jest równy 7 oraz ostatni wyraz 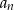 jest równy 89. Suma wszystkich wyrazów tego ciągu jest równa 2016. Oblicz, ile wyrazów ma ten ciąg.
jest równy 89. Suma wszystkich wyrazów tego ciągu jest równa 2016. Oblicz, ile wyrazów ma ten ciąg.
W skończonym ciągu arytmetycznym 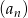 pierwszy wyraz
pierwszy wyraz 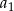 jest równy 9 oraz ostatni wyraz
jest równy 9 oraz ostatni wyraz 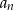 jest równy 93. Suma wszystkich wyrazów tego ciągu jest równa 2295. Oblicz, ile wyrazów ma ten ciąg.
jest równy 93. Suma wszystkich wyrazów tego ciągu jest równa 2295. Oblicz, ile wyrazów ma ten ciąg.
Liczby 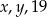 w podanej kolejności tworzą ciąg arytmetyczny, przy czym
w podanej kolejności tworzą ciąg arytmetyczny, przy czym 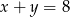 . Oblicz
. Oblicz  i
i 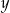 .
.
Liczby 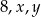 w podanej kolejności tworzą ciąg arytmetyczny, przy czym
w podanej kolejności tworzą ciąg arytmetyczny, przy czym 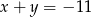 . Oblicz
. Oblicz  i
i 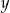 .
.
Ciąg geometryczny 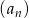 ma 100 wyrazów i są one liczbami dodatnimi. Suma wszystkich wyrazów o numerach nieparzystych jest sto razy większa od sumy wszystkich wyrazów o numerach parzystych oraz
ma 100 wyrazów i są one liczbami dodatnimi. Suma wszystkich wyrazów o numerach nieparzystych jest sto razy większa od sumy wszystkich wyrazów o numerach parzystych oraz
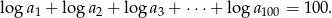
Oblicz 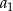 .
.
Ciąg 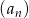 określony jest wzorem
określony jest wzorem 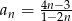 , dla
, dla 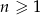 . Oblicz ile wyrazów ciągu
. Oblicz ile wyrazów ciągu 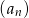 różni się od liczby -2 o więcej niż 0,1.
różni się od liczby -2 o więcej niż 0,1.
Znajdź ogólny wyraz ciągu arytmetycznego 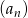 wiedząc, że
wiedząc, że 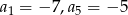 .
.
W kąt o mierze  wpisano ciąg kół w taki sposób, że pierwsze koło ma promień
wpisano ciąg kół w taki sposób, że pierwsze koło ma promień  i jest styczne do ramion kąta a każde następne koło ma mniejszy promień i jest styczne do poprzedniego koła oraz do ramion kąta. Oblicz sumę pól kół tego ciągu.
i jest styczne do ramion kąta a każde następne koło ma mniejszy promień i jest styczne do poprzedniego koła oraz do ramion kąta. Oblicz sumę pól kół tego ciągu.
W rosnącym ciągu arytmetycznym stosunek wyrazu szóstego do trzeciego równa się 7, a suma kwadratów wyrazów drugiego i czwartego równa się 40. Wyznacz pierwszy wyraz tego ciągu.
W ciągu geometrycznym 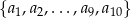 iloczyn wyrazów o numerach parzystych jest równy
iloczyn wyrazów o numerach parzystych jest równy 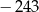 , a iloczyn wyrazów o numerach nieparzystych jest równy 7776. Wyznacz ostatni wyraz tego ciągu geometrycznego.
, a iloczyn wyrazów o numerach nieparzystych jest równy 7776. Wyznacz ostatni wyraz tego ciągu geometrycznego.
Dany jest rosnący ciąg geometryczny 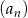 dla
dla 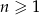 , w którym
, w którym 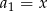 ,
, 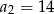 ,
, 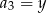 . Oblicz
. Oblicz  oraz
oraz 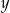 , jeżeli wiadomo, że
, jeżeli wiadomo, że 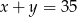 .
.

