Piąty wyraz ciągu arytmetycznego jest równy 26, a suma pięciu początkowych wyrazów tego ciągu jest równa 70. Oblicz pierwszy wyraz tego ciągu.
/Szkoła średnia/Ciągi
Siódmy wyraz ciągu arytmetycznego jest równy 34, a suma siedmiu początkowych wyrazów tego ciągu jest równa 56. Oblicz pierwszy wyraz tego ciągu.
Dwunasty wyraz ciągu arytmetycznego 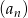 , określonego dla
, określonego dla 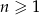 , jest równy 30, a suma jego dwunastu początkowych wyrazów jest równa 162. Oblicz pierwszy wyraz tego ciągu.
, jest równy 30, a suma jego dwunastu początkowych wyrazów jest równa 162. Oblicz pierwszy wyraz tego ciągu.
Dwudziesty wyraz ciągu arytmetycznego 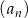 , określonego dla
, określonego dla 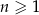 , jest równy 395, a suma jego dwudziestu początkowych wyrazów jest równa 8930. Oblicz pierwszy wyraz tego ciągu.
, jest równy 395, a suma jego dwudziestu początkowych wyrazów jest równa 8930. Oblicz pierwszy wyraz tego ciągu.
Dany jest nieskończony ciąg geometryczny 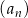 , określony dla każdej liczby naturalnej
, określony dla każdej liczby naturalnej 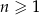 . Czwarty wyraz tego ciągu jest o
. Czwarty wyraz tego ciągu jest o  większy od drugiego wyrazu i jest mniejszy niż trzeci wyraz. Suma wszystkich wyrazów tego ciągu o numerach parzystych jest równa
większy od drugiego wyrazu i jest mniejszy niż trzeci wyraz. Suma wszystkich wyrazów tego ciągu o numerach parzystych jest równa 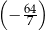 . Wyznacz wszystkie wartości
. Wyznacz wszystkie wartości  , dla których spełniona jest nierówność
, dla których spełniona jest nierówność
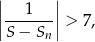
gdzie 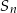 oznacza sumę
oznacza sumę  początkowych wyrazów ciągu
początkowych wyrazów ciągu 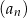 , a
, a 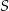 jest sumą wszystkich wszystkich wyrazów ciągu
jest sumą wszystkich wszystkich wyrazów ciągu 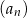 .
.
Dane są 4 liczby, z których 3 pierwsze tworzą ciąg geometryczny, a 3 ostatnie tworzą ciąg arytmetyczny. Suma pierwszej i czwartej wynosi 14, a suma drugiej i trzeciej wynosi 12. Wyznacz te 4 liczby.
Dane są 4 liczby, z których 3 pierwsze tworzą ciąg geometryczny, a 3 ostatnie tworzą ciąg arytmetyczny. Suma pierwszej i czwartej wynosi 22, a suma drugiej i trzeciej wynosi 4. Wyznacz te 4 liczby.
Liczby 3 i 7 są dwoma początkowymi wyrazami pewnego rosnącego ciągu arytmetycznego. Oblicz dwudziesty wyraz tego ciągu i sumę jego dwudziestu początkowych wyrazów.
Ciąg geometryczny 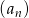 , gdzie
, gdzie 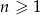 spełnia warunek
spełnia warunek 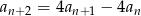 dla
dla 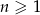 . Uzasadnij, że ciąg ten spełnia też warunek
. Uzasadnij, że ciąg ten spełnia też warunek 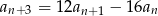 dla
dla 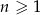 .
.
Długości trzech krawędzi prostopadłościanu wychodzących z jednego wierzchołka tworzą ciąg geometryczny, w którym największy wyraz jest o 5 większy od wyrazu najmniejszego. Objętość prostopadłościanu jest równa 216. Oblicz długości krawędzi tego prostopadłościanu.
Jaką liczbą musi być  , aby liczby:
, aby liczby: 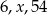 tworzyły ciąg geometryczny.
tworzyły ciąg geometryczny.
Liczby 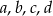 są czterema kolejnymi wyrazami ciągu geometrycznego. Trzecia liczba jest o 9 większa od pierwszej, a druga liczba jest o 18 większa od czwartej. Wyznacz te liczby.
są czterema kolejnymi wyrazami ciągu geometrycznego. Trzecia liczba jest o 9 większa od pierwszej, a druga liczba jest o 18 większa od czwartej. Wyznacz te liczby.
Wyrazami ciągu arytmetycznego 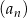 są kolejne liczby naturalne, które przy dzieleniu przez 5 dają resztę 2. Ponadto
są kolejne liczby naturalne, które przy dzieleniu przez 5 dają resztę 2. Ponadto 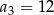 . Oblicz
. Oblicz 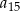 .
.
Wyrazami ciągu arytmetycznego 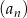 są kolejne liczby naturalne, które przy dzieleniu przez 8 dają resztę 5. Wyraz pierwszy jest mniejszy od 8. Oblicz
są kolejne liczby naturalne, które przy dzieleniu przez 8 dają resztę 5. Wyraz pierwszy jest mniejszy od 8. Oblicz 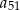 .
.
Wyrazami ciągu arytmetycznego 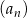 są kolejne liczby naturalne, które przy dzieleniu przez 5 dają resztę 3. Ponadto
są kolejne liczby naturalne, które przy dzieleniu przez 5 dają resztę 3. Ponadto 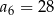 . Oblicz
. Oblicz 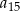 .
.
Wyrazami ciągu arytmetycznego 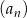 są kolejne liczby naturalne, które przy dzieleniu przez 7 dają resztę 3. Ponadto
są kolejne liczby naturalne, które przy dzieleniu przez 7 dają resztę 3. Ponadto 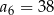 . Oblicz
. Oblicz 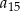 .
.
Oblicz sumę 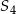 pierwszych 4 wyrazów ciągu geometrycznego
pierwszych 4 wyrazów ciągu geometrycznego 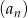 , o pierwszym wyrazie
, o pierwszym wyrazie 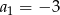 i ilorazie
i ilorazie 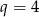 .
.
Dany jest ciąg arytmetyczny 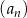 , określony dla wszystkich liczb naturalnych
, określony dla wszystkich liczb naturalnych 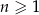 . Suma dwudziestu początkowych wyrazów tego ciągu jest równa
. Suma dwudziestu początkowych wyrazów tego ciągu jest równa 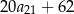 . Oblicz różnicę ciągu
. Oblicz różnicę ciągu 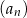 .
.
Dany jest ciąg arytmetyczny 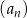 , określony dla wszystkich liczb naturalnych
, określony dla wszystkich liczb naturalnych 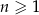 . Suma piętnastu początkowych wyrazów tego ciągu jest równa
. Suma piętnastu początkowych wyrazów tego ciągu jest równa 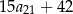 . Oblicz różnicę ciągu
. Oblicz różnicę ciągu 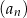 .
.
Długości boków trójkąta 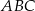 są kolejnymi wyrazami ciągu arytmetycznego, a jeden z jego kątów ma miarę
są kolejnymi wyrazami ciągu arytmetycznego, a jeden z jego kątów ma miarę 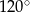 . Objętość prostopadłościanu, którego trzy krawędzie mają taką samą długość jak boki trójkąta
. Objętość prostopadłościanu, którego trzy krawędzie mają taką samą długość jak boki trójkąta 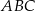 jest równa 840. Oblicz objętość największej kuli jaka może być umieszczona wewnątrz tego prostopadłościanu.
jest równa 840. Oblicz objętość największej kuli jaka może być umieszczona wewnątrz tego prostopadłościanu.
Oblicz wartości pozostałych wyrazów ciągu arytmetycznego: 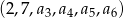 .
.
Oblicz wartości pozostałych wyrazów ciągu arytmetycznego: 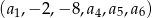 .
.
Oblicz wartości pozostałych wyrazów ciągu arytmetycznego: 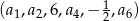 .
.
Oblicz sumę  początkowych wyrazów ciągu
początkowych wyrazów ciągu 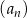 określonego dla
określonego dla 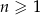 , w którym
, w którym
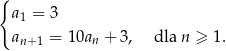
Dwudziestowyrazowy ciąg geometryczny 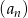 określony jest wzorem
określony jest wzorem 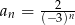 dla
dla 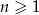 . Oblicz sumę wszystkich dodatnich wyrazów tego ciągu.
. Oblicz sumę wszystkich dodatnich wyrazów tego ciągu.
- Wyznacz liczbę naturalną
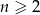 , dla której liczby
, dla której liczby 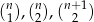 są kolejnymi wyrazami ciągu arytmetycznego;
są kolejnymi wyrazami ciągu arytmetycznego; - Dla wyznaczonej wartości
 , wyznacz liczbę naturalną
, wyznacz liczbę naturalną 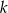 tak, aby liczby
tak, aby liczby 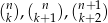 były kolejnymi wyrazami ciągu geometrycznego.
były kolejnymi wyrazami ciągu geometrycznego.
Oblicz sumę ośmiu początkowych wyrazów rosnącego ciągu geometrycznego, w którym 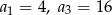 .
.
Oblicz sumę siedmiu początkowych wyrazów ciągu geometrycznego 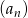 , w którym
, w którym 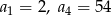 .
.
Oblicz sumę dziewięciu początkowych wyrazów rosnącego ciągu geometrycznego 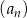 , określonego dla
, określonego dla 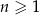 , w którym
, w którym 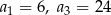 .
.
Dana jest funkcja określona wzorem 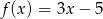 .
.
- Wyznacz ogólny wyraz ciągu
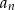 wiedząc, że:
wiedząc, że: 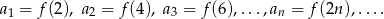
- Uzasadnij, że ciąg
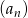 jest ciągiem arytmetycznym.
jest ciągiem arytmetycznym. - Oblicz sumę
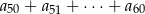 .
.
Trzeci i piąty wyraz malejącego ciągu arytmetycznego 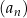 , określonego dla każdej liczby naturalnej
, określonego dla każdej liczby naturalnej 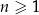 , spełniają warunek
, spełniają warunek 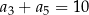 . Trzywyrazowy ciąg
. Trzywyrazowy ciąg 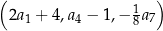 jest geometryczny. Oblicz wyrazy tego ciągu geometrycznego.
jest geometryczny. Oblicz wyrazy tego ciągu geometrycznego.
Wykaż, że liczby 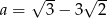 ,
, 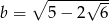 i
i 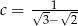 są w podanej kolejności kolejnymi wyrazami ciągu arytmetycznego.
są w podanej kolejności kolejnymi wyrazami ciągu arytmetycznego.

