Prostokąt 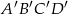 jest podobny do prostokąta
jest podobny do prostokąta 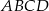 w skali
w skali 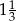 . Pole prostokąta
. Pole prostokąta 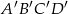 jest równe
jest równe 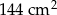 . Krótszy bok prostokąta
. Krótszy bok prostokąta 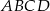 ma długość 6 cm. Oblicz długości pozostałych boków tych prostokątów.
ma długość 6 cm. Oblicz długości pozostałych boków tych prostokątów.
/Szkoła średnia/Geometria/Planimetria
Prostokąt 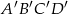 jest podobny do prostokąta
jest podobny do prostokąta 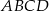 w skali
w skali 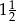 . Pole prostokąta
. Pole prostokąta 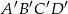 jest równe
jest równe 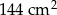 . Krótszy bok prostokąta
. Krótszy bok prostokąta 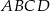 ma długość 9 cm. Oblicz długości pozostałych boków tych prostokątów.
ma długość 9 cm. Oblicz długości pozostałych boków tych prostokątów.
W trójkącie prostokątnym na rysunku 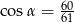 . Wiedząc, że dłuższa przyprostokątna jest o 2 cm krótsza od przeciwprostokątnej, wyznacz długości boków
. Wiedząc, że dłuższa przyprostokątna jest o 2 cm krótsza od przeciwprostokątnej, wyznacz długości boków 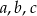 .
.
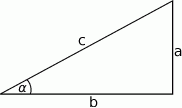
W trójkącie 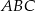 wysokość
wysokość 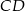 dzieli bok
dzieli bok 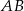 na odcinki
na odcinki 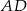 i
i 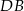 (rysunek), przy czym
(rysunek), przy czym 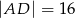 i
i 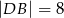 . Wykaż, że symetralna boku
. Wykaż, że symetralna boku 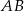 dzieli bok
dzieli bok 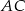 w stosunku 3:1.
w stosunku 3:1.
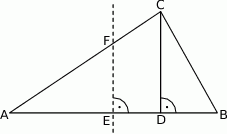
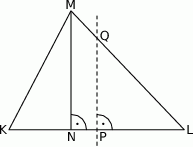
W trójkącie 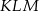 wysokość
wysokość 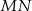 dzieli bok
dzieli bok 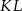 na odcinki
na odcinki 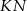 i
i 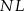 (rysunek), przy czym
(rysunek), przy czym 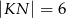 i
i 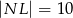 . Wykaż, że symetralna boku
. Wykaż, że symetralna boku 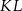 dzieli bok
dzieli bok 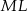 w stosunku 1:4.
w stosunku 1:4.
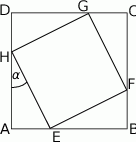
W kwadrat 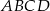 o boku długości 17 wpisano kwadrat
o boku długości 17 wpisano kwadrat 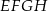 , jak pokazano na rysunku. Wiedząc, że przekątna kwadratu
, jak pokazano na rysunku. Wiedząc, że przekątna kwadratu 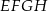 ma długość
ma długość 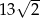 oblicz tangens kąta
oblicz tangens kąta  zaznaczonego na rysunku.
zaznaczonego na rysunku.
Na boku 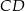 prostokąta
prostokąta 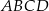 wybrano punkt
wybrano punkt 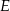 taki, że
taki, że 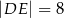 . Przekątna
. Przekątna 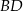 i odcinek
i odcinek 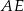 przecinają się w punkcie
przecinają się w punkcie 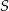 oraz
oraz 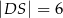 . Bok
. Bok 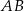 prostokąta
prostokąta 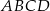 ma długość 12 (zobacz rysunek).
ma długość 12 (zobacz rysunek).
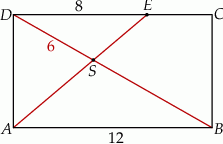
Oblicz długość odcinka 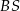 .
.
Ostrokątny trójkąt równoramienny 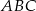 o podstawie
o podstawie 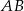 jest wpisany w okrąg o środku
jest wpisany w okrąg o środku 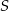 , przy czym kąt
, przy czym kąt 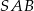 ma miarę
ma miarę 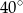 . Oblicz miarę kąta
. Oblicz miarę kąta 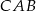 .
.
Boki prostokąta 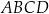 mają długości 5 i 12. Oblicz odległość wierzchołka
mają długości 5 i 12. Oblicz odległość wierzchołka 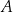 od przekątnej
od przekątnej 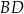 .
.
W trójkącie 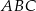 dane są:
dane są: 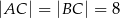 oraz
oraz 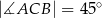 . Oblicz długość wysokości tego trójkąta poprowadzonej z wierzchołka
. Oblicz długość wysokości tego trójkąta poprowadzonej z wierzchołka 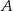 .
.
W trójkącie 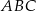 dane są:
dane są: 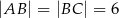 oraz
oraz 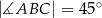 . Oblicz długość wysokości tego trójkąta poprowadzonej z wierzchołka
. Oblicz długość wysokości tego trójkąta poprowadzonej z wierzchołka 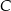 .
.
Dany jest trójkąt 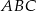 , w którym
, w którym 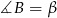 , a kąt zewnętrzny przy wierzchołku
, a kąt zewnętrzny przy wierzchołku 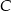 ma miarę
ma miarę  .
.
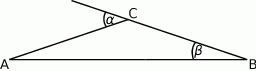
Wykaż, że jeśli 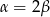 , to trójkąt
, to trójkąt 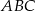 jest równoramienny.
jest równoramienny.
Uzasadnij, że jeżeli 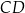 jest wysokością trójkąta prostokątnego
jest wysokością trójkąta prostokątnego 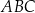 , w którym
, w którym 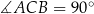 to
to 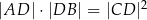 .
.

Przyprostokątne trójkąta prostokątnego 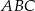 mają długości 10 i 24. Przeciwprostokątna trójkąta
mają długości 10 i 24. Przeciwprostokątna trójkąta 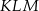 podobnego do niego ma długość 39. Oblicz pole trójkąta
podobnego do niego ma długość 39. Oblicz pole trójkąta 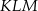 .
.
Trójkąty prostokątne 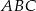 i
i 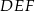 są podobne. Przyprostokątne trójkąta
są podobne. Przyprostokątne trójkąta 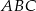 mają długości 5 i 12, a przeciwprostokątna trójkąta
mają długości 5 i 12, a przeciwprostokątna trójkąta 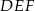 ma długość 26. Wyznacz pole trójkąta
ma długość 26. Wyznacz pole trójkąta 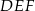 .
.
Przyprostokątne trójkąta prostokątnego 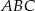 mają długości 9 i 40. Najdłuższy bok tego trójkąta jest równy najkrótszemu bokowi trójkąta
mają długości 9 i 40. Najdłuższy bok tego trójkąta jest równy najkrótszemu bokowi trójkąta 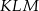 podobnego do trójkąta
podobnego do trójkąta 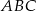 . Oblicz pole trójkąta
. Oblicz pole trójkąta 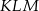 .
.
Z punktu 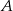 leżącego na okręgu poprowadź cięciwę
leżącego na okręgu poprowadź cięciwę 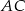 o długości równej promieniowi okręgu oraz średnicę
o długości równej promieniowi okręgu oraz średnicę 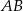 . Wyznacz miary kątów wewnętrznych trójkąta
. Wyznacz miary kątów wewnętrznych trójkąta 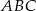 .
.
Odcinek 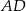 jest wysokością przedstawionego na rysunku trójkąta równoramiennego
jest wysokością przedstawionego na rysunku trójkąta równoramiennego 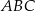 , w którym
, w którym 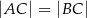 . Udowodnij, że
. Udowodnij, że 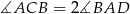 .
.
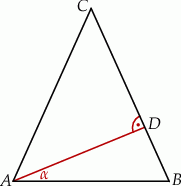
Wykaż, że miara kąta między wysokością trójkąta równoramiennego poprowadzoną do ramienia a podstawą tego trójkąta jest dwa razy mniejsza od miary kąta zawartego między ramionami tego trójkąta.
Dany jest trójkąt prostokątny o kącie ostrym 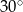 . Oblicz obwód tego trójkąta, jeżeli przeciwprostokątna ma długość 12 dm.
. Oblicz obwód tego trójkąta, jeżeli przeciwprostokątna ma długość 12 dm.
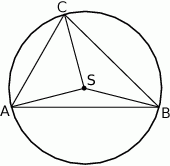
Punkt 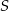 jest środkiem okręgu opisanego na trójkącie ostrokątnym
jest środkiem okręgu opisanego na trójkącie ostrokątnym 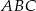 . Kąt
. Kąt 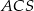 jest trzy razy większy od kąta
jest trzy razy większy od kąta 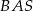 , a kąt
, a kąt 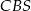 jest dwa razy większy od kąta
jest dwa razy większy od kąta 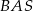 . Oblicz kąty trójkąta
. Oblicz kąty trójkąta 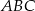 .
.
Punkt 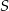 jest środkiem okręgu opisanego na trójkącie rozwartokątnym
jest środkiem okręgu opisanego na trójkącie rozwartokątnym 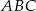 . Kąt
. Kąt 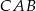 jest dwa razy większy od kąta
jest dwa razy większy od kąta 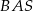 , a kąt
, a kąt 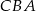 jest o
jest o 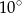 większy od kąta
większy od kąta 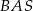 . Oblicz kąty trójkąta
. Oblicz kąty trójkąta 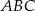 .
.
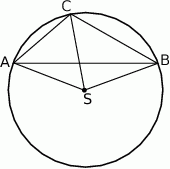
Bok 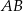 czworokąta
czworokąta 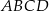 wpisanego w okrąg jest średnicą tego okręgu (zobacz rysunek). Udowodnij, że
wpisanego w okrąg jest średnicą tego okręgu (zobacz rysunek). Udowodnij, że 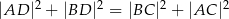 .
.
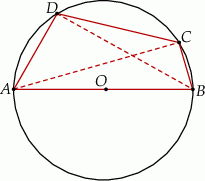
Przekątna 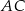 czworokąta
czworokąta 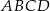 wpisanego w okrąg jest średnicą tego okręgu (zobacz rysunek). Udowodnij, że
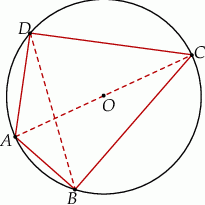
wpisanego w okrąg jest średnicą tego okręgu (zobacz rysunek). Udowodnij, że 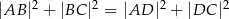 .
.
Przez punkty 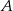 i
i 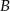 okręgu poprowadzono styczne, które przecięły się w punkcie
okręgu poprowadzono styczne, które przecięły się w punkcie 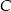 .
.
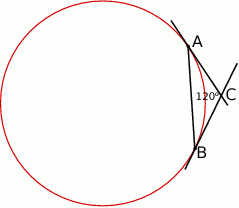
Wykaż, że jeżeli 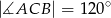 , to cięciwa
, to cięciwa 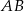 ma długość równą długości promienia okręgu.
ma długość równą długości promienia okręgu.
W trapezie 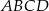 podstawy
podstawy 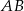 i
i 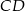 oraz ramię
oraz ramię 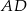 mają długości odpowiednio 15 cm, 12 cm i 6 cm. O ile centymetrów należy przedłużyć ramię
mają długości odpowiednio 15 cm, 12 cm i 6 cm. O ile centymetrów należy przedłużyć ramię 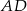 , by przecięło się z przedłużeniem ramienia
, by przecięło się z przedłużeniem ramienia 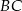 ?
?
Oblicz wysokość trapezu o podstawach długości 18 i 14 oraz ramionach długości 3.
Niech 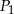 będzie prostokątem o bokach długości 3 i 8. Obok tego prostokąta rysujemy kolejne prostokąty
będzie prostokątem o bokach długości 3 i 8. Obok tego prostokąta rysujemy kolejne prostokąty 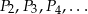 w ten sposób, że każdy z boków kolejnego prostokąta jest o 2 dłuższy od odpowiadających boków poprzedniego prostokąta.
w ten sposób, że każdy z boków kolejnego prostokąta jest o 2 dłuższy od odpowiadających boków poprzedniego prostokąta.
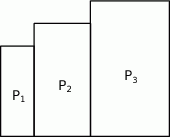
Wyznacz liczbę  , dla której obwód prostokąta
, dla której obwód prostokąta 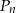 jest równy 246.
jest równy 246.

