Dane są dwa podzbiory zbioru liczb całkowitych:
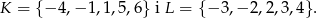
Z każdego z nich losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczb, których iloczyn jest dodatni.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dane są dwa podzbiory zbioru liczb całkowitych:
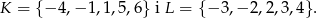
Z każdego z nich losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczb, których iloczyn jest dodatni.
Dane są dwa podzbiory zbioru liczb całkowitych:
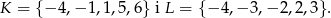
Z każdego z nich losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczb, których iloczyn jest dodatni.
Dane są dwa podzbiory zbioru liczb całkowitych:
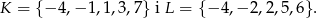
Z każdego z nich losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczb, których iloczyn jest ujemny.
Ze zbioru pięciu liczb 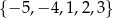 losujemy kolejno ze zwracaniem dwa razy po jednej liczbie. Zdarzenie
losujemy kolejno ze zwracaniem dwa razy po jednej liczbie. Zdarzenie  polega na wylosowaniu dwóch liczb, których iloczyn jest ujemny. Oblicz prawdopodobieństwo zdarzenia
polega na wylosowaniu dwóch liczb, których iloczyn jest ujemny. Oblicz prawdopodobieństwo zdarzenia  .
.
Do windy na parterze budynku wsiadło 8 osób, po czym każda z nich w sposób losowy wysiadła na jednym z pięciu pięter budynku. Jakie jest prawdopodobieństwo, że na jednym z pięter wysiadło co najmniej 6 osób?
Do windy na parterze budynku wsiadło 8 osób, po czym każda z nich w sposób losowy wysiadła na jednym z pięciu pięter budynku. Jakie jest prawdopodobieństwo, że na dwóch różnych piętrach wysiadły po trzy osoby?
Z liczb ośmioelementowego zbioru 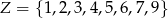 tworzymy ośmiowyrazowy ciąg, którego wyrazy się nie powtarzają. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że żadne dwie liczby parzyste nie są sąsiednimi wyrazami utworzonego ciągu. Wynik przedstaw w postaci ułamka zwykłego nieskracalnego.
tworzymy ośmiowyrazowy ciąg, którego wyrazy się nie powtarzają. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że żadne dwie liczby parzyste nie są sąsiednimi wyrazami utworzonego ciągu. Wynik przedstaw w postaci ułamka zwykłego nieskracalnego.
Ze zbioru 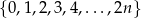 gdzie
gdzie 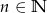 wylosowano jednocześnie 3 liczby. Prawdopodobieństwo, że suma wylosowanych liczb jest nieparzysta wynosi
wylosowano jednocześnie 3 liczby. Prawdopodobieństwo, że suma wylosowanych liczb jest nieparzysta wynosi 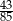 . Wyznacz ile liczb było w zbiorze.
. Wyznacz ile liczb było w zbiorze.
W urnie znajduje się 16 kul, które mogą się różnić wyłącznie kolorem. Wśród nich jest 10 kul białych i 6 kul czarnych. Z tej urny losujemy dwukrotnie jedną kulę bez zwracania. Oblicz prawdopodobieństwo wylosowania dwóch kul białych.
W urnie znajduje się 18 kul, które mogą się różnić wyłącznie kolorem. Wśród nich jest 6 kul białych i 12 kul czarnych. Z tej urny losujemy dwukrotnie jedną kulę bez zwracania. Oblicz prawdopodobieństwo wylosowania dwóch kul czarnych.
Rzucamy trzy razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo otrzymania iloczynu oczek równego 12.
Ze zbioru 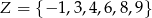 losujemy bez zwracania liczby
losujemy bez zwracania liczby  i
i 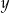 . Oblicz prawdopodobieństwa zdarzeń:
. Oblicz prawdopodobieństwa zdarzeń: 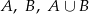 jeśli:
jeśli:
A – suma wylosowanych liczb jest nieparzysta;
B – wylosowane liczby spełniają warunek: 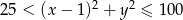 .
.
W urnie znajduje się dwa razy więcej kul białych niż czarnych. Losujemy z urny jednocześnie dwie kule. Prawdopodobieństwo wylosowania obu kul białych jest równe 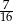 . Oblicz prawdopodobieństwo wylosowania kul różnych kolorów.
. Oblicz prawdopodobieństwo wylosowania kul różnych kolorów.
Łukasz w sposób losowy ustawia na jednej półce regału pewną liczbę książek. Wśród tych książek są trzy książki w języku angielskim, a wszystkie pozostałe są w języku polskim. Prawdopodobieństwo zdarzenia polegającego na tym, że trzy książki w języku angielskim znajdą się obok siebie jest równe 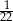 . Oblicz, ile książek w języku polskim zostało ustawionych na tej półce.
. Oblicz, ile książek w języku polskim zostało ustawionych na tej półce.
Ze zbioru wszystkich liczb naturalnych czterocyfrowych, których cyfra tysięcy i cyfra setek należą do zbioru 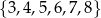 , a cyfra dziesiątek i cyfra jedności należą do zbioru
, a cyfra dziesiątek i cyfra jedności należą do zbioru 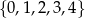 , losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy liczbę czterocyfrową, która jest podzielna przez 4.
, losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy liczbę czterocyfrową, która jest podzielna przez 4.
Jedenastu panów, wśród których są  ,
, 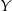 i
i 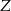 , ustawiamy losowo w szeregu. Oblicz prawdopodobieństwo, że pan
, ustawiamy losowo w szeregu. Oblicz prawdopodobieństwo, że pan 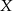 będzie stał obok pana
będzie stał obok pana 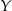 i pan
i pan 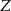 nie będzie stał obok pana
nie będzie stał obok pana 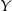 .
.
Ze zbioru liczb dwucyfrowych losujemy jedną liczbę. Jakie jest prawdopodobieństwo, że iloczyn cyfr wylosowanej liczby jest dodatnią liczbą złożoną?
Na stole leżało 14 banknotów: 2 banknoty o nominale 100 zł, 2 banknoty o nominale 50 zł i 10 banknotów o nominale 20 zł. Wiatr zdmuchnął na podłogę 5 banknotów. Oblicz prawdopodobieństwo tego, że na podłodze leży dokładnie 130 zł. Odpowiedź podaj w postaci ułamka nieskracalnego.
Ze zbioru liczb 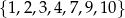 losujemy dwie liczby (mogą się powtarzać). Oblicz prawdopodobieństwo, że suma wylosowanych liczb jest parzysta.
losujemy dwie liczby (mogą się powtarzać). Oblicz prawdopodobieństwo, że suma wylosowanych liczb jest parzysta.
Dany jest pięcioelementowy zbiór 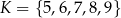 . Wylosowanie każdej liczby z tego zbioru jest jednakowo prawdopodobne. Ze zbioru
. Wylosowanie każdej liczby z tego zbioru jest jednakowo prawdopodobne. Ze zbioru 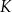 losujemy ze zwracaniem kolejno dwa razy po jednej liczbie i zapisujemy je w kolejności losowania. Oblicz prawdopodobieństwo zdarzenia
losujemy ze zwracaniem kolejno dwa razy po jednej liczbie i zapisujemy je w kolejności losowania. Oblicz prawdopodobieństwo zdarzenia 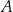 polegającego na tym, że suma wylosowanych liczb jest liczbą parzystą.
polegającego na tym, że suma wylosowanych liczb jest liczbą parzystą.
Na loterii jest  losów, w tym 4 wygrywające. Kupujemy 2 losy. Dla jakiej liczby
losów, w tym 4 wygrywające. Kupujemy 2 losy. Dla jakiej liczby  prawdopodobieństwo otrzymania co najmniej jednego losu wygrywającego jest równe
prawdopodobieństwo otrzymania co najmniej jednego losu wygrywającego jest równe 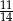 ?
?
W urnie znajduje się 5 kul białych i 3 czarne. Wyjmujemy losowo 4 kule. Oblicz prawdopodobieństwo, że wśród wyjętych są przynajmniej 2 kule czarne.
Ze zbioru 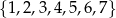 losujemy liczbę
losujemy liczbę  , a ze zbioru
, a ze zbioru 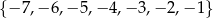 liczbę
liczbę 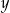 . Oblicz prawdopodobieństwo tego, że
. Oblicz prawdopodobieństwo tego, że 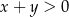 .
.
Ze zbioru 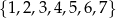 losujemy liczbę
losujemy liczbę  , a ze zbioru
, a ze zbioru 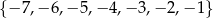 liczbę
liczbę 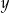 . Oblicz prawdopodobieństwo tego, że
. Oblicz prawdopodobieństwo tego, że 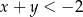 .
.
Ze zbioru 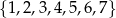 losujemy liczbę
losujemy liczbę  , a ze zbioru
, a ze zbioru 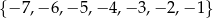 liczbę
liczbę 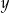 . Oblicz prawdopodobieństwo tego, że
. Oblicz prawdopodobieństwo tego, że 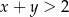 .
.
Ze zbioru liczb 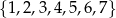 losujemy kolejno dwa razy po jednej liczbie bez zwracania. Oblicz prawdopodobieństwo zdarzenia
losujemy kolejno dwa razy po jednej liczbie bez zwracania. Oblicz prawdopodobieństwo zdarzenia 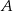 polegającego na tym, że pierwsza z wylosowanych liczb jest nieparzysta, a ich iloczyn jest większy od 10.
polegającego na tym, że pierwsza z wylosowanych liczb jest nieparzysta, a ich iloczyn jest większy od 10.
Ze zbioru liczb 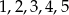 losujemy kolejno trzy razy po jednej liczbie bez zwracania tworząc liczbę trzycyfrową. Oblicz prawdopodobieństwo zdarzenia
losujemy kolejno trzy razy po jednej liczbie bez zwracania tworząc liczbę trzycyfrową. Oblicz prawdopodobieństwo zdarzenia  – otrzymana liczba jest mniejsza od 432.
– otrzymana liczba jest mniejsza od 432.
Ze zbioru liczb 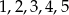 losujemy kolejno trzy razy po jednej liczbie bez zwracania tworząc liczbę trzycyfrową. Oblicz prawdopodobieństwo zdarzenia
losujemy kolejno trzy razy po jednej liczbie bez zwracania tworząc liczbę trzycyfrową. Oblicz prawdopodobieństwo zdarzenia 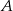 – otrzymana liczba jest większa od 324.
– otrzymana liczba jest większa od 324.
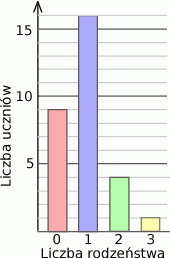
W pewnym liceum, wśród uczniów 30 osobowej klasy (każdy uczeń pochodzi z innej rodziny), zebrano dane na temat posiadanego rodzeństwa. Wyniki badań przedstawiono na diagramie.
Dane są trzy sześcienne kostki do gry: czerwona, niebieska i zielona. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że przy jednokrotnym rzucie trzema kostkami liczba otrzymana na niebieskiej kostce jest większa niż suma liczb otrzymanych na dwóch pozostałych kostkach.
