Dany jest sześcian 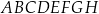 o krawędzi długości 1. Punkty
o krawędzi długości 1. Punkty 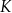 i
i 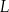 są środkami odpowiednio krawędzi
są środkami odpowiednio krawędzi 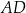 i
i 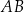 , a punkt
, a punkt 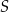 jest środkiem odcinka
jest środkiem odcinka 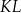 . Punkt
. Punkt 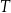 jest takim punktem krawędzi
jest takim punktem krawędzi 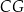 , że
, że 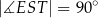 (zobacz rysunek).
(zobacz rysunek).
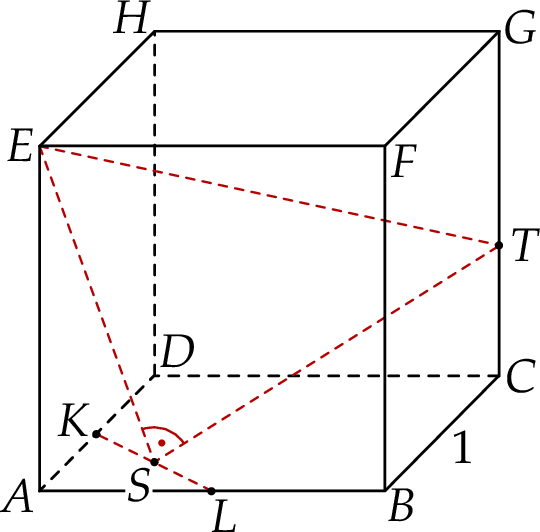
Oblicz odległość punktu  od środka odcinka
od środka odcinka 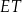 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dany jest sześcian 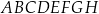 o krawędzi długości 1. Punkty
o krawędzi długości 1. Punkty 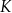 i
i 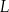 są środkami odpowiednio krawędzi
są środkami odpowiednio krawędzi 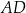 i
i 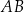 , a punkt
, a punkt 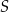 jest środkiem odcinka
jest środkiem odcinka 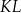 . Punkt
. Punkt 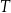 jest takim punktem krawędzi
jest takim punktem krawędzi 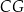 , że
, że 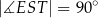 (zobacz rysunek).
(zobacz rysunek).

Oblicz odległość punktu 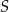 od środka odcinka
od środka odcinka 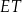 .
.
W trójkąt prostokątny o przyprostokątnych o długościach 2 i 4 wpisano prostokąt w ten sposób, że dwa jego boki leżą na przyprostokątnych trójkąta, a jeden z wierzchołków prostokąta leży na przeciwprostokątnej trójkąta. Prostokąt ten obraca się dookoła prostej, zawierającej dłuższą przyprostokątną trójkąta, tworząc walec. Oblicz, który z walców, otrzymanych w powyższy sposób, posiada największe pole powierzchni bocznej i oblicz jego objętość.
Dany jest prostokątny arkusz kartonu o długości 80 cm i szerokości 50 cm. W czterech rogach tego arkusza wycięto kwadratowe naroża (zobacz rysunek).

Następnie zagięto karton wzdłuż linii przerywanych, tworząc w ten sposób prostopadłościenne pudełko (bez przykrywki). Oblicz długość boku wyciętych kwadratowych naroży, dla której objętość otrzymanego pudełka jest największa. Oblicz tę objętość.
Dany jest prostokątny arkusz kartonu o długości 64 cm i szerokości 40 cm. Po dwóch stronach tego arkusza wycięto prostokąty, w których stosunek boków jest równy 1:2 (zacieniowane prostokąty na rysunku).

Następnie zagięto karton wzdłuż linii przerywanych, tworząc w ten sposób prostopadłościenne pudełko (bez przykrywki). Oblicz długości boków wyciętych prostokątów, dla których objętość otrzymanego pudełka jest największa. Oblicz tę objętość.
Krawędź boczna ostrosłupa prawidłowego trójkątnego jest nachylona do płaszczyzny podstawy pod kątem  . Przez krawędź podstawy tego ostrosłupa poprowadzono płaszczyznę, która jest nachylona do płaszczyzny podstawy pod katem
. Przez krawędź podstawy tego ostrosłupa poprowadzono płaszczyznę, która jest nachylona do płaszczyzny podstawy pod katem 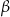 , i która przecina przeciwległą krawędź ostrosłupa (zobacz rysunek).
, i która przecina przeciwległą krawędź ostrosłupa (zobacz rysunek).
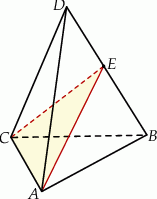
Oblicz stosunek pola powierzchni otrzymanego przekroju do pola powierzchni podstawy ostrosłupa jeżeli wiadomo, że 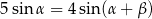 .
.
Metalową kulę o promieniu 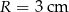 przetopiono na stożek. Tworząca stożka jest nachylona do płaszczyzny podstawy pod kątem
przetopiono na stożek. Tworząca stożka jest nachylona do płaszczyzny podstawy pod kątem  , takim, że
, takim, że 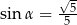 . Wyznacz promień podstawy tego stożka.
. Wyznacz promień podstawy tego stożka.
Stożek ma wysokość 10 cm. Pole przekroju osiowego tego stożka jest równe 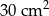 . Jaką długość ma tworząca tego stożka?
. Jaką długość ma tworząca tego stożka?
Krawędź sześcianu ma długość  . Oblicz pole przekroju tego sześcianu płaszczyzną przechodzącą przez przekątną podstawy i środki dwóch kolejnych krawędzi górnej podstawy.
. Oblicz pole przekroju tego sześcianu płaszczyzną przechodzącą przez przekątną podstawy i środki dwóch kolejnych krawędzi górnej podstawy.
W sześcian o krawędzi 4 wpisano kulę styczną do trzech ścian sześcianu oraz przechodzącą przez środek sześcianu. Oblicz promień tej kuli.
Każda krawędź graniastosłupa prawidłowego sześciokątnego ma długość równą 6. Oblicz cosinus kąta nachylenia dłuższej przekątnej tego graniastosłupa do płaszczyzny podstawy graniastosłupa.
Podstawą graniastosłupa prostego 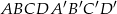 jest równoległobok
jest równoległobok 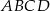 o bokach długości
o bokach długości 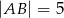 i
i 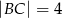 . Oblicz długość wysokości
. Oblicz długość wysokości 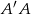 graniastosłupa jeżeli
graniastosłupa jeżeli 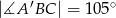 oraz
oraz 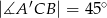 .
.
Wśród wszystkich graniastosłupów prawidłowych sześciokątnych, w których suma długości wszystkich krawędzi jest równa 24, jest taki, który ma największe pole powierzchni bocznej. Oblicz długość krawędzi podstawy tego graniastosłupa.
W ostrosłup prawidłowy czworokątny wpisujemy graniastosłupy prawidłowe czworokątne w ten sposób, że dolna podstawa graniastosłupa zawiera się podstawie ostrosłupa, a każdy z wierzchołków górnej podstawy należy do jednej z krawędzi bocznych ostrosłupa. Wiedząc, że każda z krawędzi ostrosłupa ma długość 6, oblicz jaka jest maksymalna możliwa powierzchnia boczna graniastosłupa.
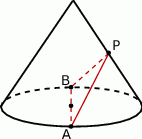
Środek 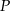 tworzącej stożka połączono z końcami
tworzącej stożka połączono z końcami  i
i 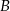 średnicy koła w podstawie stożka tak, że
średnicy koła w podstawie stożka tak, że 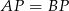 . Wiedząc, że kąt rozwarcia stożka jest równy
. Wiedząc, że kąt rozwarcia stożka jest równy 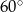 , oblicz kąty trójkąta
, oblicz kąty trójkąta 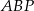 .
.
Tangens kąta nachylenia ściany bocznej do płaszczyzny podstawy ostrosłupa prawidłowego czworokątnego jest równy  . Oblicz tangens nachylenia krawędzi bocznej do płaszczyzny podstawy tego ostrosłupa.
. Oblicz tangens nachylenia krawędzi bocznej do płaszczyzny podstawy tego ostrosłupa.
W ostrosłupie prawidłowym trójkątnym  cosinus kąta nachylenia krawędzi bocznej do płaszczyzny podstawy jest równy
cosinus kąta nachylenia krawędzi bocznej do płaszczyzny podstawy jest równy  . Wykaż, że pole powierzchni bocznej tego ostrosłupa stanowi
. Wykaż, że pole powierzchni bocznej tego ostrosłupa stanowi  jego pola powierzchni całkowitej.
jego pola powierzchni całkowitej.
Graniastosłup prawidłowy trójkątny o krawędzi podstawy 4 cm i wysokości 10 cm przecięto płaszczyzną zawierającą wysokość podstawy i jedną z krawędzi bocznych. Jakie pole ma ten przekrój?
Wysokość ostrosłupa prawidłowego sześciokątnego jest równa 6 cm i stanowi  długości krawędzi podstawy.
długości krawędzi podstawy.
Wysokość ostrosłupa prawidłowego sześciokątnego jest równa 9 cm i stanowi  długości krawędzi podstawy.
długości krawędzi podstawy.
Każda ściana graniastosłupa jest rombem o boku długości  i kącie ostrym o mierze
i kącie ostrym o mierze 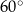 . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa.
Oblicz wysokość graniastosłupa sześciokątnego prawidłowego, wiedząc, że krawędź podstawy ma długość 5 cm, zaś najdłuższa przekątna graniastosłupa jest 4 razy dłuższa od najkrótszej przekątnej podstawy.
Oblicz wysokość graniastosłupa sześciokątnego prawidłowego, wiedząc, że krawędź podstawy ma długość 4 cm, zaś najdłuższa przekątna graniastosłupa jest 5 razy dłuższa od najkrótszej przekątnej podstawy.
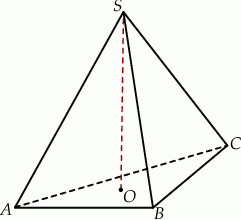
W graniastosłupie prawidłowym sześciokątnym 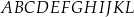 płaszczyzna
płaszczyzna 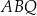 przechodzi przez krawędź
przechodzi przez krawędź 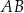 i przez środek
i przez środek 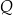 krawędzi
krawędzi 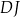 (zobacz rysunek).
(zobacz rysunek).
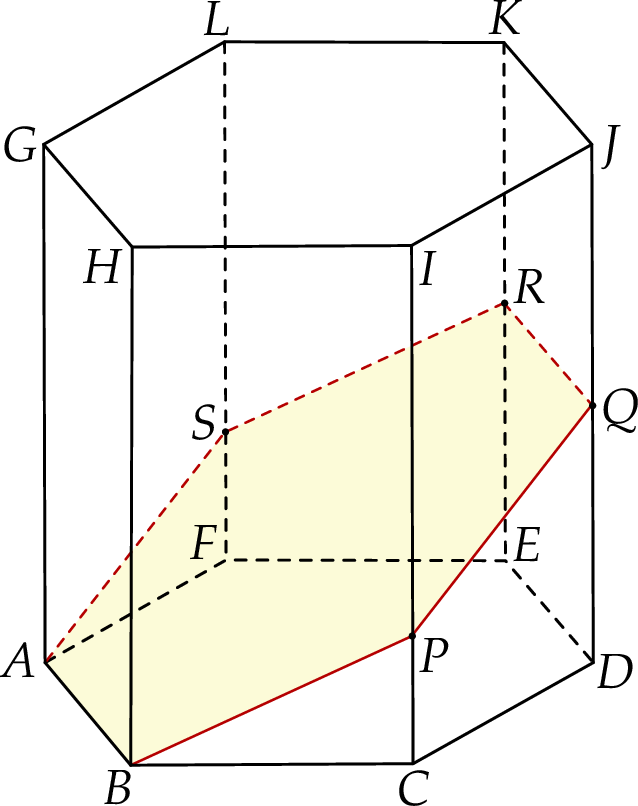
Stosunek pola przekroju graniastosłupa płaszczyzną  do pola jego podstawy jest równy
do pola jego podstawy jest równy 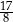 . Oblicz objętość graniastosłupa
. Oblicz objętość graniastosłupa 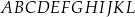 , jeżeli jego krawędź boczna ma długość
, jeżeli jego krawędź boczna ma długość 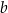 .
.
