W graniastosłupie prawidłowym trójkątnym poprowadzono płaszczyznę 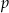 wyznaczoną przez wysokość dolnej podstawy i ten z wierzchołków górnej podstawy, że płaszczyzna
wyznaczoną przez wysokość dolnej podstawy i ten z wierzchołków górnej podstawy, że płaszczyzna 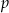 z płaszczyzną podstawy graniastosłupa tworzy kąt ostry
z płaszczyzną podstawy graniastosłupa tworzy kąt ostry  taki, że
taki, że 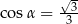 . Pole przekroju graniastosłupa wyznaczonego przez płaszczyznę
. Pole przekroju graniastosłupa wyznaczonego przez płaszczyznę 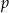 jest równe
jest równe 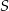 . Oblicz objętość graniastosłupa.
. Oblicz objętość graniastosłupa.
/Szkoła średnia/Geometria/Stereometria
Objętość graniastosłupa prawidłowego czworokątnego jest równa 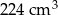 , a promień okręgu opisanego na podstawie ma długość 4 cm. Wyznacz miarę kąta między przekątnymi sąsiednich ścian bocznych wychodzącymi z tego samego wierzchołka graniastosłupa. Wynik podaj z dokładnością do
, a promień okręgu opisanego na podstawie ma długość 4 cm. Wyznacz miarę kąta między przekątnymi sąsiednich ścian bocznych wychodzącymi z tego samego wierzchołka graniastosłupa. Wynik podaj z dokładnością do 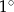 .
.
Dane są dwie bryły: stożek, w którym długość promienia podstawy jest równa 2 dm i wysokość ma długość 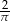 dm oraz ostrosłup prawidłowy trójkątny, w którym krawędź podstawy ma długość 4 dm. Wiedząc, że objętości tych brył są równe, wyznacz kąt nachylenia ściany bocznej ostrosłupa do jego podstawy.
dm oraz ostrosłup prawidłowy trójkątny, w którym krawędź podstawy ma długość 4 dm. Wiedząc, że objętości tych brył są równe, wyznacz kąt nachylenia ściany bocznej ostrosłupa do jego podstawy.
Podstawą ostrosłupa 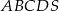 jest kwadrat
jest kwadrat 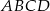 . Trójkąt równoramienny
. Trójkąt równoramienny 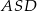 ma ramię długości 15 i jest prostopadły do podstawy ostrosłupa. Krawędź
ma ramię długości 15 i jest prostopadły do podstawy ostrosłupa. Krawędź 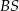 ma długość 17. Oblicz pole przekroju ostrosłupa płaszczyzną
ma długość 17. Oblicz pole przekroju ostrosłupa płaszczyzną 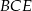 , gdzie
, gdzie 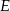 jest środkiem krawędzi
jest środkiem krawędzi 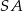 .
.
W pojemniku o kształcie walca o promieniu podstawy 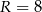 umieszczono dwie kule o promieniu
umieszczono dwie kule o promieniu 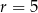 , w ten sposób, że są do siebie styczne i każda z nich dotyka powierzchni bocznej walca, jak na rysunku. Jaka co najmniej musi być wysokość pojemnika, aby kule całkowicie się w nim mieściły. Oblicz objętość tego walca.
, w ten sposób, że są do siebie styczne i każda z nich dotyka powierzchni bocznej walca, jak na rysunku. Jaka co najmniej musi być wysokość pojemnika, aby kule całkowicie się w nim mieściły. Oblicz objętość tego walca.
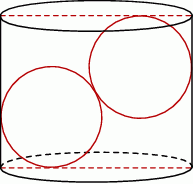
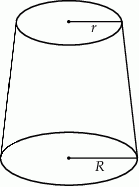
Objętość stożka ściętego (przedstawionego na rysunku) można obliczyć ze wzoru 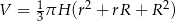 , gdzie
, gdzie  i
i 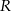 są promieniami podstaw (
są promieniami podstaw (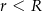 ), a
), a 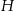 jest wysokością bryły. Dany jest stożek ścięty, którego wysokość jest równa 10, objętość
jest wysokością bryły. Dany jest stożek ścięty, którego wysokość jest równa 10, objętość 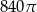 , a
, a 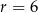 . Oblicz cosinus kąta nachylenia przekątnej przekroju osiowego tej bryły do jednej z jej podstaw.
. Oblicz cosinus kąta nachylenia przekątnej przekroju osiowego tej bryły do jednej z jej podstaw.
We wnętrzu sześcianu umieszczono czworościan foremny w ten sposób, że wszystkie krawędzie czworościanu są przekątnymi ścian bocznych sześcianu. Wyznacz stosunek objętości czworościanu do objętości sześcianu.
W graniastosłupie prawidłowym czworokątnym 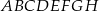 przekątna
przekątna 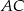 podstawy ma długość 4. Kąt
podstawy ma długość 4. Kąt 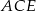 jest równy
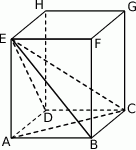
jest równy 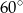 . Oblicz objętość ostrosłupa
. Oblicz objętość ostrosłupa 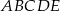 przedstawionego na poniższym rysunku.
przedstawionego na poniższym rysunku.
Dany jest ostrosłup prawidłowy sześciokątny. Wysokość ściany bocznej tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem 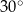 i ma długość równą 6 (zobacz rysunek).
i ma długość równą 6 (zobacz rysunek).
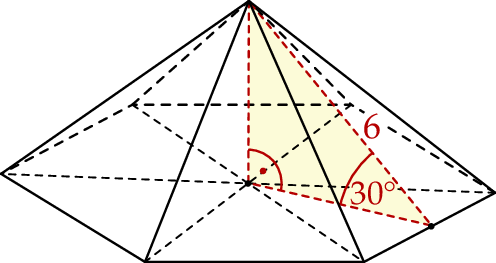
Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa.
Dany jest zbiór wszystkich graniastosłupów prawidłowych sześciokątnych, których suma długości wszystkich krawędzi jest równa 216. Oblicz długość krawędzi podstawy i wysokość tego z danych graniastosłupów, który ma największe pole powierzchni bocznej.
Dany jest graniastosłup prawidłowy czworokątny, którego suma długości wszystkich krawędzi wynosi 12.
- Napisz wzór funkcji
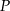 wyrażającej pole powierzchni całkowitej graniastosłupa, w zależności od długości krawędzi podstawy
wyrażającej pole powierzchni całkowitej graniastosłupa, w zależności od długości krawędzi podstawy  . Podaj dziedzinę funkcji
. Podaj dziedzinę funkcji 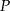 .
. - Wyznacz długości krawędzi graniastosłupa, dla których pole powierzchni całkowitej jest największe.
W graniastosłupie prawidłowym sześciokątnym wszystkie krawędzie mają jednakową długość. Oblicz objętość tego graniastosłupa jeżeli jego pole powierzchni całkowitej jest równe 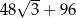 .
.
Przekątna przekroju osiowego walca ma długość 5 cm i jest nachylona do płaszczyzny podstawy pod kątem 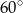 . Jaką długość ma promień podstawy tego walca? Jaka jest jego wysokość?
. Jaką długość ma promień podstawy tego walca? Jaka jest jego wysokość?
Krawędź boczna ostrosłupa prawidłowego czworokątnego jest nachylona do płaszczyzny podstawy pod kątem  takim, że
takim, że 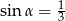 . Oblicz cosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.
. Oblicz cosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.
W ostrosłupie prawidłowym trójkątnym wysokość ściany bocznej ma długość 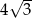 , a ściana boczna jest nachylona do płaszczyzny podstawy pod kątem
, a ściana boczna jest nachylona do płaszczyzny podstawy pod kątem 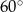 . Oblicz objętość ostrosłupa.
. Oblicz objętość ostrosłupa.
Trójkąt równoboczny 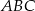 jest podstawą ostrosłupa prawidłowego
jest podstawą ostrosłupa prawidłowego 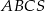 , w którym ściana boczna jest nachylona do płaszczyzny podstawy pod kątem
, w którym ściana boczna jest nachylona do płaszczyzny podstawy pod kątem 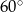 , a krawędź boczna ma długość
, a krawędź boczna ma długość 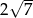 (zobacz rysunek). Oblicz objętość tego ostrosłupa.
(zobacz rysunek). Oblicz objętość tego ostrosłupa.
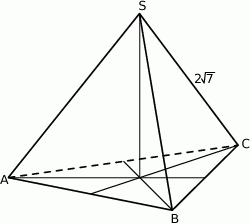
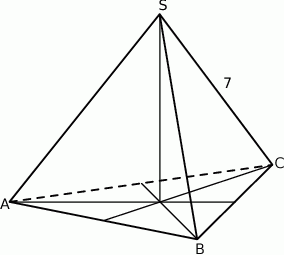
Trójkąt równoboczny 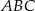 jest podstawą ostrosłupa prawidłowego
jest podstawą ostrosłupa prawidłowego 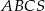 , w którym ściana boczna jest nachylona do płaszczyzny podstawy pod kątem
, w którym ściana boczna jest nachylona do płaszczyzny podstawy pod kątem 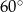 , a krawędź boczna ma długość 7 (zobacz rysunek). Oblicz objętość tego ostrosłupa.
, a krawędź boczna ma długość 7 (zobacz rysunek). Oblicz objętość tego ostrosłupa.
Objętość graniastosłupa prawidłowego czworokątnego jest równa 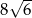 . Przekątna tego graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem
. Przekątna tego graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem 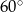 . Oblicz pole powierzchni całkowitej tego graniastosłupa.
. Oblicz pole powierzchni całkowitej tego graniastosłupa.

