W ostrosłup prawidłowy czworokątny wpisano sześcian tak, że jego cztery wierzchołki należą do wysokości ścian bocznych ostrosłupa, a pozostałe do płaszczyzny podstawy. Oblicz stosunek objętości ostrosłupa do objętości sześcianu jeżeli kąt nachylenia ściany bocznej do płaszczyzny podstawy jest równy  .
.
/Szkoła średnia/Geometria/Stereometria
W ostrosłupie 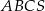 podstawa
podstawa 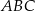 jest trójkątem równobocznym o boku długości
jest trójkątem równobocznym o boku długości  . Krawędź
. Krawędź 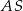 jest prostopadła do płaszczyzny podstawy. Odległość wierzchołka
jest prostopadła do płaszczyzny podstawy. Odległość wierzchołka 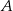 od ściany
od ściany 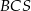 jest równa
jest równa 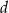 . Wyznacz objętość tego ostrosłupa.
. Wyznacz objętość tego ostrosłupa.
W ostrosłupie prawidłowym czworokątnym 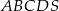 (zobacz rysunek) przekątna
(zobacz rysunek) przekątna 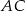 podstawy ma długość
podstawy ma długość 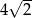 . Kąt
. Kąt 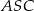 między przeciwległymi krawędziami bocznymi ostrosłupa ma miarę
między przeciwległymi krawędziami bocznymi ostrosłupa ma miarę 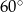 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
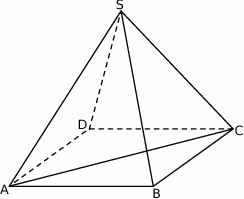
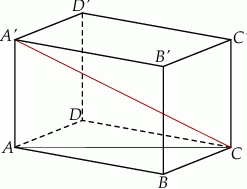
W ostrosłupie prawidłowym czworokątnym 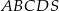 (zobacz rysunek) przekątna
(zobacz rysunek) przekątna 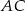 podstawy ma długość 6. Kąt
podstawy ma długość 6. Kąt 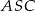 między przeciwległymi krawędziami bocznymi ostrosłupa ma miarę
między przeciwległymi krawędziami bocznymi ostrosłupa ma miarę 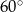 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
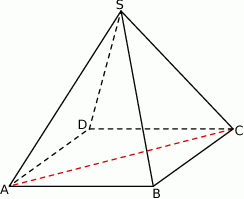
Dany jest ostrosłup prawidłowy trójkątny 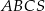 o podstawie
o podstawie 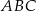 . Krawędź podstawy tego ostrosłupa ma długość
. Krawędź podstawy tego ostrosłupa ma długość  . Ściana boczna jest nachylona do płaszczyzny podstawy pod kątem
. Ściana boczna jest nachylona do płaszczyzny podstawy pod kątem  takim, że
takim, że 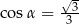 . Przez środek
. Przez środek 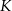 krawędzi
krawędzi 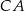 i środek
i środek 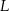 krawędzi
krawędzi 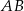 poprowadzono płaszczyznę
poprowadzono płaszczyznę 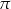 prostopadłą do płaszczyzny
prostopadłą do płaszczyzny 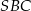 . Oblicz pole otrzymanego przekroju.
. Oblicz pole otrzymanego przekroju.
Podstawą graniastosłupa prostego 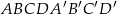 jest romb
jest romb 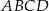 . Przekątna
. Przekątna 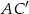 tego graniastosłupa ma długość 8 i jest nachylona do płaszczyzny podstawy pod kątem
tego graniastosłupa ma długość 8 i jest nachylona do płaszczyzny podstawy pod kątem 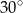 , a przekątna
, a przekątna 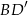 jest nachylona do tej płaszczyzny pod kątem
jest nachylona do tej płaszczyzny pod kątem 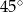 . Oblicz pole powierzchni całkowitej tego graniastosłupa.
. Oblicz pole powierzchni całkowitej tego graniastosłupa.
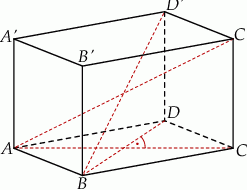
Podstawą graniastosłupa prostego 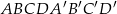 jest romb
jest romb 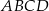 . Przekątna
. Przekątna 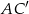 tego graniastosłupa ma długość 6 i jest nachylona do płaszczyzny podstawy pod kątem
tego graniastosłupa ma długość 6 i jest nachylona do płaszczyzny podstawy pod kątem 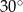 , a przekątna
, a przekątna 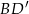 ma długość
ma długość 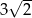 . Oblicz pole powierzchni całkowitej tego graniastosłupa.
. Oblicz pole powierzchni całkowitej tego graniastosłupa.
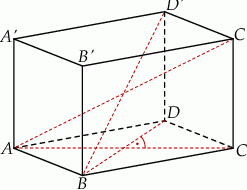
Podstawą graniastosłupa prostego 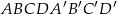 jest romb
jest romb 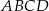 . Przekątna
. Przekątna 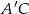 tego graniastosłupa ma długość 6 i jest nachylona do płaszczyzny podstawy pod kątem
tego graniastosłupa ma długość 6 i jest nachylona do płaszczyzny podstawy pod kątem 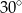 , a objętość graniastosłupa jest równa
, a objętość graniastosłupa jest równa 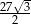 . Oblicz pole powierzchni całkowitej tego graniastosłupa.
. Oblicz pole powierzchni całkowitej tego graniastosłupa.
Powierzchnia boczna walca po rozwinięciu jest prostokątem, którego przekątna ma długość 18 cm i tworzy z bokiem odpowiadającym wysokości walca kąt o mierze 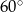 . Oblicz objętość walca.
. Oblicz objętość walca.
Powierzchnia boczna walca po rozwinięciu jest prostokątem, którego przekątna ma długość 6 cm i tworzy z bokiem odpowiadającym wysokości walca kąt o mierze 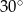 . Oblicz objętość walca.
. Oblicz objętość walca.
Oblicz objętość graniastosłupa prawidłowego trójkątnego, w którym krawędź podstawy ma długość 1, a przekątna ściany bocznej tworzy z sąsiednią ścianą kąt o mierze 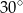 .
.
W graniastosłupie prawidłowym trójkątnym krawędź podstawy ma długość 4, a przekątna 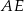 , ściany
, ściany 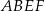 jest nachylona do ściany
jest nachylona do ściany 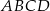 pod kątem ostrym
pod kątem ostrym  takim, że
takim, że 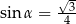 .
.
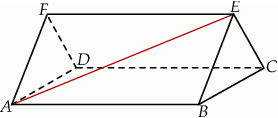
- Zaznacz na rysunku kąt
 .
. - Oblicz objętość graniastosłupa.
Dany jest ostrosłup prawidłowy czworokątny 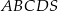 o podstawie
o podstawie 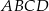 i polu powierzchni bocznej równym
i polu powierzchni bocznej równym 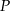 . Kąt między wysokościami sąsiednich ścian bocznych poprowadzonych z wierzchołka
. Kąt między wysokościami sąsiednich ścian bocznych poprowadzonych z wierzchołka 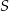 ma miarę
ma miarę 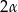 . Objętość tego ostrosłupa jest równa
. Objętość tego ostrosłupa jest równa 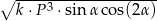 , gdzie
, gdzie 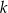 jest stałym współczynnikiem liczbowym. Oblicz współczynnik
jest stałym współczynnikiem liczbowym. Oblicz współczynnik 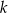 .
.
W ostrosłup prawidłowy czworokątny wpisano kulę o promieniu  . Ściana boczna ostrosłupa nachylona jest do płaszczyzny podstawy pod kątem
. Ściana boczna ostrosłupa nachylona jest do płaszczyzny podstawy pod kątem 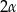 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
W ostrosłup prawidłowy czworokątny wpisano kulę o promieniu 2. Ściana boczna ostrosłupa nachylona jest do płaszczyzny podstawy pod kątem 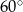 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Pole powierzchni bocznej graniastosłupa prawidłowego czworokątnego jest 6 razy większe, od jego pola podstawy, a objętość tego graniastosłupa jest równa 12. Oblicz długość krawędzi podstawy oraz długość przekątnej tego graniastosłupa. Zapisz obliczenia.
Na płaskiej powierzchni położono trzy kule 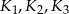 , każda o promieniu 2 tak, że kule
, każda o promieniu 2 tak, że kule 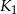 i
i 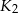 są styczne w punkcie
są styczne w punkcie 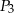 , kule
, kule 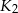 i
i 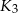 są styczne w punkcie
są styczne w punkcie 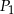 , a kule
, a kule 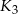 i
i 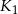 są styczne w punkcie
są styczne w punkcie 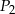 . Następnie położono na tych kulach kulę
. Następnie położono na tych kulach kulę 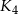 o promieniu 3, która jest styczna do kul
o promieniu 3, która jest styczna do kul 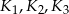 odpowiednio w punktach
odpowiednio w punktach 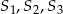 .
.
- Uzasadnij, że odcinki
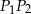 i
i 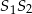 są równoległe.
są równoległe. - Oblicz obwód trapezu
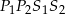 .
.
Każda krawędź graniastosłupa trójkątnego ma długość 26. Ściana boczna 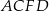 jest prostopadła do płaszczyzny podstawy
jest prostopadła do płaszczyzny podstawy 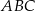 , a krawędź
, a krawędź 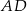 jest nachylona do płaszczyzny podstawy pod katem
jest nachylona do płaszczyzny podstawy pod katem  takim, że
takim, że 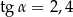 (zobacz rysunek).
(zobacz rysunek).
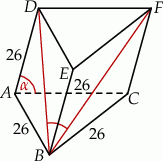
Oblicz cosinus kąta 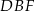 .
.
Dany jest graniastosłup prawidłowy trójkątny 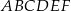 o podstawach
o podstawach 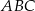 i
i 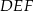 i krawędziach bocznych
i krawędziach bocznych 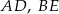 i
i 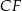 . Oblicz pole trójkąta
. Oblicz pole trójkąta 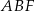 wiedząc, że
wiedząc, że 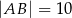 i
i 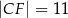 . Narysuj ten graniastosłup i zaznacz na nim trójkąt
. Narysuj ten graniastosłup i zaznacz na nim trójkąt 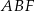 .
.
Dany jest graniastosłup prawidłowy trójkątny 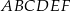 o podstawach
o podstawach 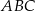 i
i 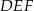 i krawędziach bocznych
i krawędziach bocznych 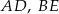 i
i 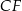 . Oblicz pole trójkąta
. Oblicz pole trójkąta 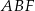 wiedząc, że
wiedząc, że 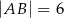 i
i 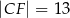 . Narysuj ten graniastosłup i zaznacz na nim trójkąt
. Narysuj ten graniastosłup i zaznacz na nim trójkąt 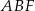 .
.
Pole powierzchni całkowitej 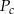 stożka oraz jego pole podstawy
stożka oraz jego pole podstawy 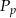 spełniają równanie
spełniają równanie 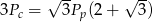 . Oblicz miarę kąta rozwarcia stożka.
. Oblicz miarę kąta rozwarcia stożka.
Oblicz objętość ostrosłupa prawidłowego trójkątnego o krawędzi podstawy 6 cm i krawędzi bocznej 12 cm.
Oblicz objętość ostrosłupa prawidłowego trójkątnego o krawędzi podstawy długości 6 cm i krawędzi bocznej długości 8 cm.
Każda z krawędzi podstawy trójkątnej ostrosłupa ma długość 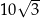 , a każda jego krawędź boczna ma długość 15. Oblicz wysokość tego ostrosłupa.
, a każda jego krawędź boczna ma długość 15. Oblicz wysokość tego ostrosłupa.
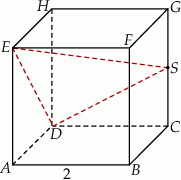
Dany jest sześcian 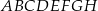 o krawędzi długości 2. Punkt
o krawędzi długości 2. Punkt 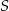 jest środkiem krawędzi
jest środkiem krawędzi 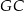 (zobacz rysunek). Oblicz promień okręgu opisanego na trójkącie
(zobacz rysunek). Oblicz promień okręgu opisanego na trójkącie 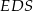 .
.
W ostrosłupie prawidłowym trójkątnym krawędź podstawy ma długość  . Kąt między krawędzią boczną, a krawędzią podstawy ma miarę
. Kąt między krawędzią boczną, a krawędzią podstawy ma miarę 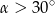 . Oblicz objętość ostrosłupa.
. Oblicz objętość ostrosłupa.
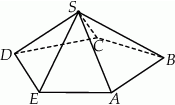
Dany jest ostrosłup o podstawie pięciokątnej 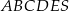 (zobacz rysunek). Każda ze ścian bocznych tego ostrosłupa jest trójkątem o polu trzy razy mniejszym niż pole pięciokąta
(zobacz rysunek). Każda ze ścian bocznych tego ostrosłupa jest trójkątem o polu trzy razy mniejszym niż pole pięciokąta 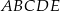 . Pole powierzchni całkowitej tego ostrosłupa jest równe 136. Oblicz pole jego podstawy.
. Pole powierzchni całkowitej tego ostrosłupa jest równe 136. Oblicz pole jego podstawy.
Dany jest sześcian 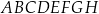 o krawędzi długości 1. Punkty
o krawędzi długości 1. Punkty 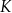 i
i 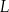 są środkami odpowiednio krawędzi
są środkami odpowiednio krawędzi 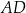 i
i 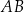 , a punkt
, a punkt 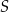 jest środkiem odcinka
jest środkiem odcinka 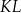 . Punkt
. Punkt 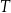 jest takim punktem krawędzi
jest takim punktem krawędzi 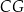 , że
, że 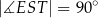 (zobacz rysunek).
(zobacz rysunek).
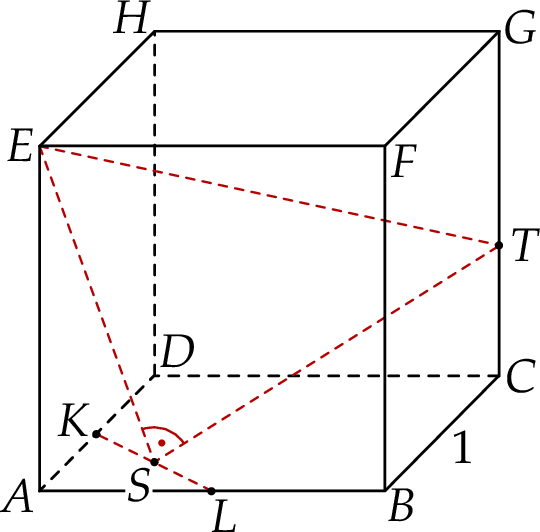
Oblicz odległość punktu 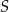 od środka odcinka
od środka odcinka 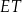 .
.

