Podstawą ostrosłupa jest romb, którego pole wynosi 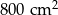 , a kąt ostry rombu ma miarę
, a kąt ostry rombu ma miarę 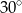 . Wysokość ostrosłupa jest równa 24 cm, a spodek tej wysokości jest środkiem okręgu wpisanego w podstawę. Oblicz:
. Wysokość ostrosłupa jest równa 24 cm, a spodek tej wysokości jest środkiem okręgu wpisanego w podstawę. Oblicz:
- promień tego okręgu,
- pole powierzchni bocznej ostrosłupa.

 . Oblicz tangens kąta ostrego
. Oblicz tangens kąta ostrego 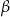 , jaki tworzy z płaszczyzną podstawy płaszczyzna przechodząca przez wierzchołek ostrosłupa oraz przez środki dwóch sąsiednich boków podstawy.
, jaki tworzy z płaszczyzną podstawy płaszczyzna przechodząca przez wierzchołek ostrosłupa oraz przez środki dwóch sąsiednich boków podstawy. 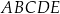 , w których krawędź boczna ma długość
, w których krawędź boczna ma długość 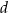 (zobacz rysunek).
(zobacz rysunek). 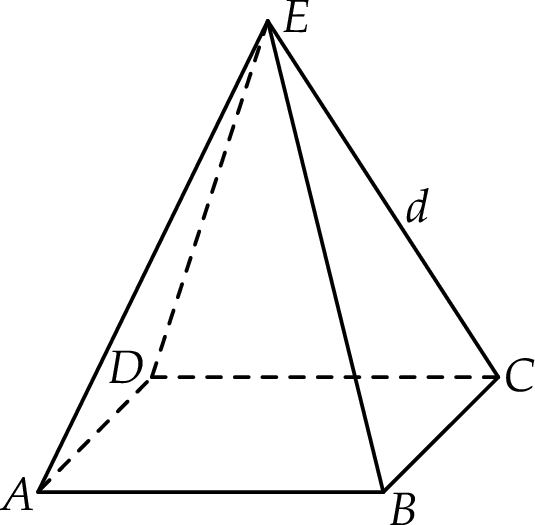
 ostrosłupa od jego wysokości
ostrosłupa od jego wysokości  i podaj dziedzinę funkcji
i podaj dziedzinę funkcji 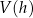 .
.  , taki że
, taki że 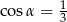 . Pole podstawy tego graniastosłupa wynosi
. Pole podstawy tego graniastosłupa wynosi 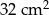 . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa.  , taki że
, taki że 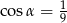 . Pole podstawy tego graniastosłupa wynosi
. Pole podstawy tego graniastosłupa wynosi 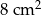 . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa. 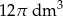 , a cosinus kąta
, a cosinus kąta  między wysokością, a tworzącą wynosi 0,8. Oblicz:
między wysokością, a tworzącą wynosi 0,8. Oblicz:  jest trójkąt równoramienny
jest trójkąt równoramienny  , w którym
, w którym 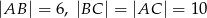 , a wszystkie krawędzie boczne tworzą z płaszczyzną podstawy kąt
, a wszystkie krawędzie boczne tworzą z płaszczyzną podstawy kąt 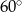 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa. 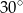 . Oblicz długość krawędzi sześcianu, którego objętość jest równa objętości tego ostrosłupa.
. Oblicz długość krawędzi sześcianu, którego objętość jest równa objętości tego ostrosłupa. 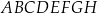 o podstawie prostokątnej
o podstawie prostokątnej 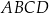 . Przekątne
. Przekątne 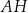 i
i 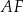 ścian bocznych tworzą kąt ostry o mierze
ścian bocznych tworzą kąt ostry o mierze  takiej, że
takiej, że 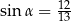 (zobacz rysunek). Pole trójkąta
(zobacz rysunek). Pole trójkąta 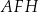 jest równe 26,4. Oblicz wysokość
jest równe 26,4. Oblicz wysokość 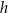 tego graniastosłupa.
tego graniastosłupa. 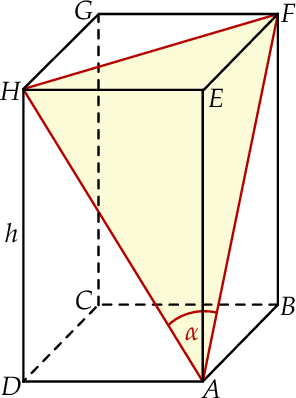
 przecięto płaszczyzną przechodzącą przez przekątną podstawy, która jest nachylona do płaszczyzny podstawy pod kątem
przecięto płaszczyzną przechodzącą przez przekątną podstawy, która jest nachylona do płaszczyzny podstawy pod kątem 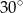 . Oblicz pole powstałego przekroju.
. Oblicz pole powstałego przekroju. 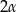 wpisano kulę. Oblicz stosunek objętości stożka do objętości kuli.
wpisano kulę. Oblicz stosunek objętości stożka do objętości kuli.  . Wyznacz stosunek objętości tej kuli do objętości stożka.
. Wyznacz stosunek objętości tej kuli do objętości stożka. 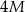 , a jedna z jego ścian na pole powierzchni dwa razy większe od innej ściany tego prostopadłościanu. Oblicz jaka jest powierzchnia całkowita tego prostopadłościanu, jeżeli jego objętość jest największa możliwa.
, a jedna z jego ścian na pole powierzchni dwa razy większe od innej ściany tego prostopadłościanu. Oblicz jaka jest powierzchnia całkowita tego prostopadłościanu, jeżeli jego objętość jest największa możliwa. 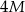 , a jedna z jego ścian na pole powierzchni trzy razy większe od innej ściany tego prostopadłościanu. Oblicz jaka jest powierzchnia całkowita tego prostopadłościanu, jeżeli jego objętość jest największa możliwa.
, a jedna z jego ścian na pole powierzchni trzy razy większe od innej ściany tego prostopadłościanu. Oblicz jaka jest powierzchnia całkowita tego prostopadłościanu, jeżeli jego objętość jest największa możliwa.  takim, że
takim, że 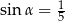 . Wyznacz objętość tego graniastosłupa.
. Wyznacz objętość tego graniastosłupa.  takim, że
takim, że 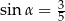 . Wyznacz objętość tego graniastosłupa.
. Wyznacz objętość tego graniastosłupa. 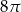 , w którym stosunek wysokości do promienia podstawy jest równy 3:8. Oblicz pole powierzchni bocznej tego stożka.
, w którym stosunek wysokości do promienia podstawy jest równy 3:8. Oblicz pole powierzchni bocznej tego stożka. 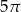 , w którym stosunek wysokości do promienia podstawy jest równy 5:9. Oblicz pole powierzchni bocznej tego stożka.
, w którym stosunek wysokości do promienia podstawy jest równy 5:9. Oblicz pole powierzchni bocznej tego stożka. 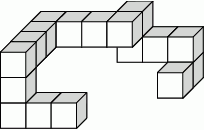
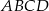 jest trójkąt
jest trójkąt 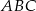 , a krawędź
, a krawędź 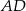 jest wysokością ostrosłupa. Oblicz pole powierzchni całkowitej ostrosłupa
jest wysokością ostrosłupa. Oblicz pole powierzchni całkowitej ostrosłupa 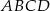 , jeśli wiadomo, że jego objętość jest równa 48 oraz
, jeśli wiadomo, że jego objętość jest równa 48 oraz 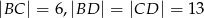 . Podaj wszystkie możliwe odpowiedzi.
. Podaj wszystkie możliwe odpowiedzi.  . Oblicz pole powierzchni całkowitej tego graniastosłupa.
. Oblicz pole powierzchni całkowitej tego graniastosłupa.  . Oblicz pole powierzchni całkowitej tego graniastosłupa.
. Oblicz pole powierzchni całkowitej tego graniastosłupa. 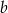 . Wyznacz wysokość tego stożka, którego objętość jest największa. Oblicz objętość tego stożka.
. Wyznacz wysokość tego stożka, którego objętość jest największa. Oblicz objętość tego stożka. 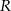 , wiedząc, że kąt rozwarcia stożka ma miarę
, wiedząc, że kąt rozwarcia stożka ma miarę 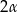 .
. 