Podstawą ostrosłupa jest równoramienny trójkąt prostokątny. Każda krawędź boczna ma długość 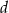 i jest nachylona do płaszczyzny podstawy pod kątem
i jest nachylona do płaszczyzny podstawy pod kątem  . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
/Szkoła średnia/Geometria/Stereometria
W ostrosłupie prawidłowym trójkątnym krawędź podstawy ma długość  . Ściany boczne są trójkątami ostrokątnymi. Miara kąta między sąsiednimi ścianami bocznymi jest równa
. Ściany boczne są trójkątami ostrokątnymi. Miara kąta między sąsiednimi ścianami bocznymi jest równa 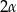 . Wyznacz objętość tego ostrosłupa.
. Wyznacz objętość tego ostrosłupa.
Dany jest ostrosłup prawidłowy trójkątny. Promień okręgu opisanego na podstawie tego ostrosłupa jest równy 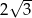 . Ściana boczna jest nachylona do płaszczyzny podstawy ostrosłupa pod kątem
. Ściana boczna jest nachylona do płaszczyzny podstawy ostrosłupa pod kątem 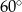 . Oblicz objętość i pole powierzchni bocznej tego ostrosłupa.
. Oblicz objętość i pole powierzchni bocznej tego ostrosłupa.
Romb o kącie ostrym 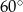 , obraca się wokół boku. Oblicz pole powierzchni i objętość otrzymanej bryły wiedząc że długość boku rombu jest równa
, obraca się wokół boku. Oblicz pole powierzchni i objętość otrzymanej bryły wiedząc że długość boku rombu jest równa  .
.
Krótsza przekątna graniastosłupa prawidłowego sześciokątnego tworzy z płaszczyzną podstawy kąt 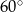 . Przekątna ściany bocznej ma długość
. Przekątna ściany bocznej ma długość 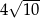 .
.
- Oblicz objętość i pole powierzchni całkowitej tego graniastosłupa.
- Oblicz cosinus kąta między krótszymi przekątnymi graniastosłupa wychodzącymi z jednego wierzchołka.
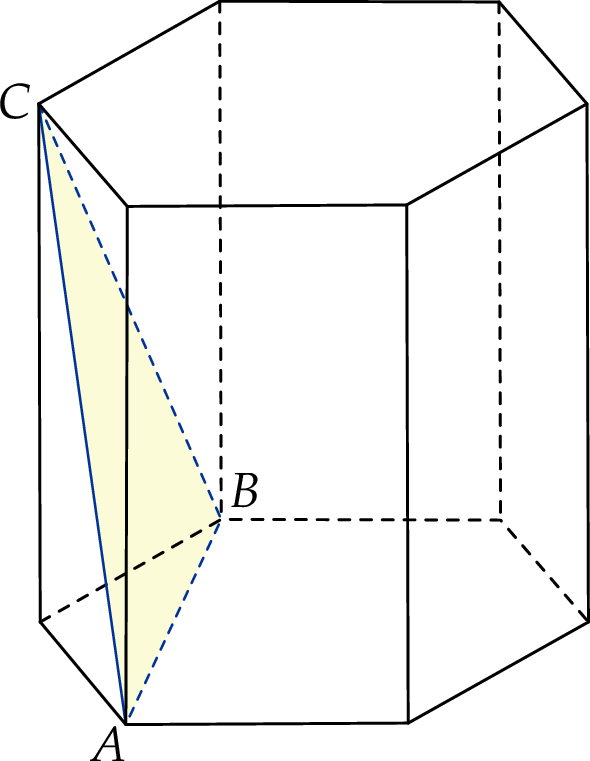
W graniastosłupie prawidłowym sześciokątnym płaszczyzna 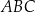 zawierająca przekątne sąsiednich ścian bocznych, wychodzących z tego samego wierzchołka, jest nachylona do podstawy graniastosłupa pod kątem
zawierająca przekątne sąsiednich ścian bocznych, wychodzących z tego samego wierzchołka, jest nachylona do podstawy graniastosłupa pod kątem 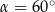 . Pole przekroju graniastosłupa tą płaszczyzną równa się
. Pole przekroju graniastosłupa tą płaszczyzną równa się 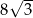 . Zaznacz na poniższym rysunku kąt
. Zaznacz na poniższym rysunku kąt  . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa.
W ostrosłupie prawidłowym czworokątnym o objętości 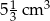 wysokość jest 2 razy dłuższa od krawędzi podstawy. Oblicz pole powierzchni tego ostrosłupa
wysokość jest 2 razy dłuższa od krawędzi podstawy. Oblicz pole powierzchni tego ostrosłupa
W graniastosłupie prawidłowym trójkątnym o krawędzi podstawy 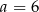 przekątna ściany bocznej tworzy z drugą ścianą boczną kąt o mierze
przekątna ściany bocznej tworzy z drugą ścianą boczną kąt o mierze 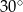 . Oblicz
. Oblicz
- długość przekątnej ściany bocznej,
- długość wysokości graniastosłupa,
- objętość i pole powierzchni całkowitej.
W graniastosłupie prawidłowym trójkątnym o krawędzi podstawy 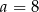 przekątna ściany bocznej tworzy z drugą ścianą boczną kąt o mierze
przekątna ściany bocznej tworzy z drugą ścianą boczną kąt o mierze 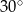 . Oblicz
. Oblicz
- długość przekątnej ściany bocznej,
- długość wysokości graniastosłupa,
- objętość i pole powierzchni całkowitej.
Graniastosłup prawidłowy czworokątny o krawędzi podstawy równej  i wysokości dwa razy dłuższej od krawędzi podstawy, przecięto płaszczyzną przechodzącą przez przekątną podstawy i nachyloną do podstawy pod kątem miary
i wysokości dwa razy dłuższej od krawędzi podstawy, przecięto płaszczyzną przechodzącą przez przekątną podstawy i nachyloną do podstawy pod kątem miary 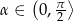 . Oblicz pole otrzymanego przekroju. Rozważ wszystkie możliwe przypadki.
. Oblicz pole otrzymanego przekroju. Rozważ wszystkie możliwe przypadki.
Graniastosłup prawidłowy czworokątny o krawędzi podstawy równej  i wysokości trzy razy dłuższej od podstawy, przecięto płaszczyzną przechodzącą przez przekątną podstawy i nachyloną do podstawy pod kątem miary
i wysokości trzy razy dłuższej od podstawy, przecięto płaszczyzną przechodzącą przez przekątną podstawy i nachyloną do podstawy pod kątem miary 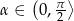 . Oblicz pole otrzymanego przekroju. Rozważ wszystkie możliwe przypadki.
. Oblicz pole otrzymanego przekroju. Rozważ wszystkie możliwe przypadki.
Dany jest ostrosłup prawidłowy trójkątny 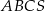 o podstawie
o podstawie 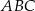 i polu powierzchni bocznej równym
i polu powierzchni bocznej równym 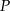 . Kąt między wysokościami sąsiednich ścian bocznych poprowadzonych z wierzchołka
. Kąt między wysokościami sąsiednich ścian bocznych poprowadzonych z wierzchołka 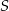 ma miarę
ma miarę 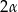 . Objętość tego ostrosłupa jest równa
. Objętość tego ostrosłupa jest równa 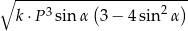 , gdzie
, gdzie 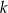 jest stałym współczynnikiem liczbowym. Oblicz współczynnik
jest stałym współczynnikiem liczbowym. Oblicz współczynnik 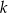 .
.
W graniastosłupie prawidłowym trójkątnym o krawędzi podstawy równej 6, poprowadzono płaszczyznę przechodzącą przez wysokość podstawy oraz wierzchołek górnej podstawy. Wiedząc, że płaszczyzna ta tworzy z płaszczyzną podstawy kąt o mierze 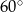 oblicz pole otrzymanego przekroju.
oblicz pole otrzymanego przekroju.
Z kartonu w kształcie trójkąta równobocznego o boku długości 120 cm odcięto trzy identyczne czworokąty w narożnikach (zobacz rysunek).
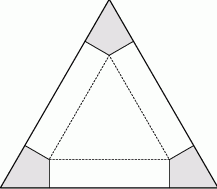
Następnie zagięto karton wzdłuż linii przerywanych, tworząc w ten sposób pudełko w kształcie graniastosłupa trójkątnego prostego (bez przykrywki). Oblicz długość krawędzi podstawy tego pudełka, którego objętość jest największa. Oblicz tę objętość.
Z kawałka blachy w kształcie sześciokąta foremnego o boku długości 60 cm robimy pudełko o sześciokątnym dnie (otwarte od góry) w następujący sposób: przy każdym wierzchołku odcinamy taki sam deltoid, tnąc w tej samej odległości od wierzchołka raz prostopadle do jednego, a drugi raz do drugiego boku, następnie zaginamy blachę wzdłuż przerywanych linii i lutujemy krawędzie (zobacz rysunek).
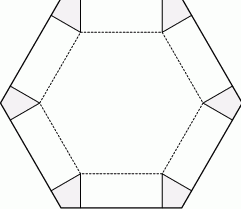
Oblicz długość krawędzi podstawy tego pudełka, którego objętość jest największa. Oblicz tę objętość.
Wysokość stożka podzielono na trzy równe odcinki i przez punkty podziału poprowadzono płaszczyzny równoległe do podstawy. Oblicz stosunek objętości powstałych brył.
Podstawą ostrosłupa 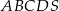 jest prostokąt
jest prostokąt 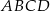 , w którym
, w którym 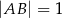 ,
, 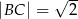 . Wszystkie krawędzie boczne tego ostrosłupa mają długość 1. Wyznacz cosinus kąta między dwiema sąsiednimi ścianami bocznymi tego ostrosłupa.
. Wszystkie krawędzie boczne tego ostrosłupa mają długość 1. Wyznacz cosinus kąta między dwiema sąsiednimi ścianami bocznymi tego ostrosłupa.
Przedstawiona na rysunku bryła to stożek ścięty płaszczyzną równoległą do jego płaszczyzny podstawy. Wysokość tej bryły jest równa 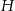 , a
, a  i
i 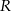 (
(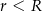 ) są promieniami podstaw. Oblicz objętość tej bryły.
) są promieniami podstaw. Oblicz objętość tej bryły.
W graniastosłupie czworokątnym prawidłowym przekątna o długości 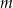 jest nachylona do płaszczyzny podstawy pod kątem
jest nachylona do płaszczyzny podstawy pod kątem  . Wiadomo, że
. Wiadomo, że 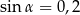 . Wyznacz objętość tego graniastosłupa.
. Wyznacz objętość tego graniastosłupa.
Podstawą ostrosłupa 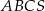 jest trójkąt równoramienny
jest trójkąt równoramienny 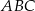 , w którym
, w którym 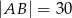 ,
, 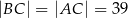 . Spodek wysokości ostrosłupa należy do jego podstawy, a każda wysokość ściany bocznej poprowadzona z wierzchołka
. Spodek wysokości ostrosłupa należy do jego podstawy, a każda wysokość ściany bocznej poprowadzona z wierzchołka 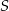 ma długość 26. Oblicz objętość tego ostrosłupa.
ma długość 26. Oblicz objętość tego ostrosłupa.
Podstawą ostrosłupa 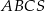 jest trójkąt równoramienny
jest trójkąt równoramienny 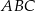 , w którym
, w którym 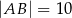 ,
, 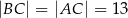 i spodek wysokości ostrosłupa należy do jego podstawy. Każda wysokość ściany bocznej poprowadzona z wierzchołka
i spodek wysokości ostrosłupa należy do jego podstawy. Każda wysokość ściany bocznej poprowadzona z wierzchołka 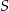 ma długość
ma długość 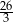 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Oblicz objętość czworościanu foremnego o krawędzi  .
.
W stożek o promieniu podstawy długości 9 i wysokości 12 wpisano walec, w ten sposób, że jedna podstawa walca zawiera się w podstawie stożka, a brzeg jego drugiej podstawy zawiera się w powierzchni bocznej stożka. Oblicz długość promienia podstawy i długość wysokości walca, wiedząc że pole powierzchni bocznej walca wynosi 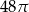 .
.
W stożek o promieniu podstawy długości 10 i wysokości 15 wpisano walec, w ten sposób, że jedna podstawa walca zawiera się w podstawie stożka, a brzeg jego drugiej podstawy zawiera się w powierzchni bocznej stożka. Oblicz długość promienia podstawy i długość wysokości walca, wiedząc że pole powierzchni bocznej walca wynosi 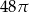 .
.
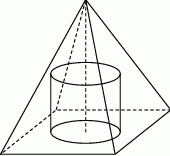
W ostrosłup prawidłowy czworokątny o wysokości 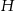 i krawędzi podstawy
i krawędzi podstawy  wpisano walec, którego podstawa zawiera się w podstawie ostrosłupa, i którego oś symetrii pokrywa się z osią symetrii ostrosłupa. Jakie powinny być wymiary tego walca, aby jego objętość była największa możliwa? Oblicz tę największą objętość.
wpisano walec, którego podstawa zawiera się w podstawie ostrosłupa, i którego oś symetrii pokrywa się z osią symetrii ostrosłupa. Jakie powinny być wymiary tego walca, aby jego objętość była największa możliwa? Oblicz tę największą objętość.