W ostrosłupie prawidłowym trójkątnym krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem 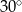 . Wyznacz cosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.
. Wyznacz cosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.
/Szkoła średnia/Geometria/Stereometria
Objętość stożka, w którym wysokość jest równa promieniowi podstawy, jest równa 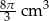 . Oblicz pole powierzchni całkowitej tego stożka. Przyjmując przybliżenie
. Oblicz pole powierzchni całkowitej tego stożka. Przyjmując przybliżenie 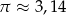 podaj wynik z dokładnością do 0,1.
podaj wynik z dokładnością do 0,1.
Podstawą ostrosłupa 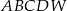 jest prostokąt
jest prostokąt 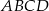 . Krawędź boczna
. Krawędź boczna 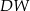 jest wysokością tego ostrosłupa. Krawędzie boczne
jest wysokością tego ostrosłupa. Krawędzie boczne 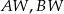 i
i 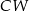 mają następujące długości:
mają następujące długości: 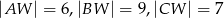 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Podstawą ostrosłupa  jest kwadrat
jest kwadrat 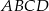 o polu 2. Krawędź boczna
o polu 2. Krawędź boczna 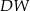 jest wysokością tego ostrosłupa. Długości krawędzi bocznych
jest wysokością tego ostrosłupa. Długości krawędzi bocznych 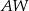 i
i 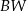 spełniają warunek
spełniają warunek 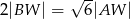 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
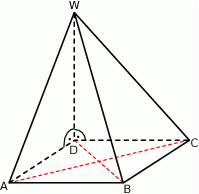
Podstawą ostrosłupa  jest kwadrat
jest kwadrat  . Krawędź boczna
. Krawędź boczna 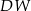 jest wysokością tego ostrosłupa. Krawędzie boczne
jest wysokością tego ostrosłupa. Krawędzie boczne 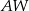 i
i 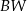 mają następujące długości:
mają następujące długości: 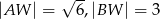 . Oblicz pole powierzchni całkowitej tego ostrosłupa.
. Oblicz pole powierzchni całkowitej tego ostrosłupa.
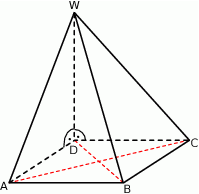
Wysokość ostrosłupa prawidłowego trójkątnego jest równa 4, a krawędź podstawy ma długość 1. Ostrosłup przecięto płaszczyzną, która przechodzi przez krawędź podstawy oraz jest prostopadła do przeciwległej krawędzi bocznej. Oblicz pole powierzchni tego przekroju.
W graniastosłupie prawidłowym sześciokątnym poprowadzono płaszczyznę, która przechodzi przez krawędź podstawy oraz przez środek symetrii graniastosłupa. Płaszczyzna ta wyznacza przekrój o polu równym 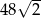 . Stosunek wysokości graniastosłupa do długości krawędzi podstawy jest równy
. Stosunek wysokości graniastosłupa do długości krawędzi podstawy jest równy 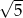 . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa.
W ostrosłupie trójkątnym wszystkie krawędzie boczne i dwie krawędzie podstawy mają długość 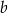 , a kąt między równymi bokami podstawy ma miarę
, a kąt między równymi bokami podstawy ma miarę  . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
W stożek o promieniu podstawy 6 i wysokości 8 wpisujemy graniastosłupy prawidłowe sześciokątne tak, że jedna podstawa jest zawarta w podstawie stożka, a pozostałe wierzchołki należą do powierzchni bocznej stożka. Oblicz objętość graniastosłupa o największym polu powierzchni bocznej.
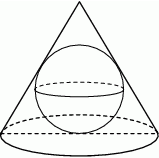
W stożek o wysokości 10 wpisano kulę o promieniu 4. Oblicz pole powierzchni całkowitej stożka.
Podstawą graniastosłupa prostego o objętości 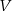 jest równoległobok o bokach długości
jest równoległobok o bokach długości  i
i 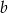 . Wykaż, że pole powierzchni bocznej tego graniastosłupa jest nie mniejsze niż
. Wykaż, że pole powierzchni bocznej tego graniastosłupa jest nie mniejsze niż 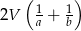 .
.
Dany jest graniastosłup czworokątny prosty 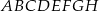 o podstawach
o podstawach 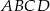 i
i 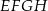 oraz krawędziach bocznych
oraz krawędziach bocznych 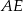 ,
, 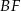 ,
, 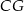 ,
, 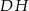 . Podstawa
. Podstawa 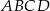 graniastosłupa jest rombem o boku długości 8 cm i kątach ostrych
graniastosłupa jest rombem o boku długości 8 cm i kątach ostrych 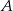 i
i 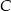 o mierze
o mierze 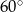 . Przekątna graniastosłupa
. Przekątna graniastosłupa 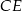 jest nachylona do płaszczyzny podstawy pod kątem
jest nachylona do płaszczyzny podstawy pod kątem 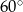 . Sporządź rysunek pomocniczy i zaznacz na nim wymienione w zadaniu kąty. Oblicz objętość tego graniastosłupa.
. Sporządź rysunek pomocniczy i zaznacz na nim wymienione w zadaniu kąty. Oblicz objętość tego graniastosłupa.
W graniastosłupie prostym o podstawie rombu krótsza przekątna podstawy ma długość 6 cm i tworzy z krawędzią podstawy kąt 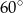 . Kąt między krótszą przekątną rombu i krótszą przekątną graniastosłupa ma miarę
. Kąt między krótszą przekątną rombu i krótszą przekątną graniastosłupa ma miarę 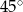 . Oblicz objętość graniastosłupa.
. Oblicz objętość graniastosłupa.
Podstawą graniastosłupa prostego jest romb. Krótsza przekątna rombu tworzy z krawędzią podstawy kąt 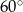 i ma długość
i ma długość 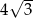 . Dłuższa przekątna graniastosłupa tworzy z dłuższą przekątną rombu kąt
. Dłuższa przekątna graniastosłupa tworzy z dłuższą przekątną rombu kąt 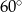 . Oblicz objętość graniastosłupa.
. Oblicz objętość graniastosłupa.
Rozważmy wszystkie graniastosłupy prawidłowe trójkątne o objętości 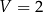 . Wyznacz długości krawędzi tego z rozważanych graniastosłupów, którego pole powierzchni całkowitej jest najmniejsze. Oblicz to najmniejsze pole.
. Wyznacz długości krawędzi tego z rozważanych graniastosłupów, którego pole powierzchni całkowitej jest najmniejsze. Oblicz to najmniejsze pole.
Rozważmy wszystkie graniastosłupy prawidłowe czworokątne o objętości 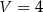 . Wyznacz długości krawędzi tego z rozważanych graniastosłupów, którego pole powierzchni całkowitej jest najmniejsze. Oblicz to najmniejsze pole.
. Wyznacz długości krawędzi tego z rozważanych graniastosłupów, którego pole powierzchni całkowitej jest najmniejsze. Oblicz to najmniejsze pole.
Połówkę koła o promieniu 12 zwinięto w stożek. Oblicz objętość i kąt rozwarcia tego stożka jeżeli długość łuku tej połówki koła jest obwodem podstawy, a jej promień jest tworzącą stożka.
Długości krawędzi podstawy prostopadłościanu są równe 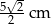 , a krawędź boczna ma długość 2 cm. Oblicz pole przekroju tego graniastosłupa płaszczyzną zawierającą przekątną podstawy i nachyloną do płaszczyzny podstawy pod kątem
, a krawędź boczna ma długość 2 cm. Oblicz pole przekroju tego graniastosłupa płaszczyzną zawierającą przekątną podstawy i nachyloną do płaszczyzny podstawy pod kątem 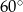 . Sporządź rysunek i zaznacz na nim przekrój oraz kąt jego nachylenia do płaszczyzny podstawy.
. Sporządź rysunek i zaznacz na nim przekrój oraz kąt jego nachylenia do płaszczyzny podstawy.
Mówimy, że walec jest wpisany w graniastosłup, jeżeli podstawy walca są zawarte w podstawach graniastosłupa, a powierzchnia boczna walca jest styczna do każdej ze ścian bocznych graniastosłupa (zobacz rysunek).
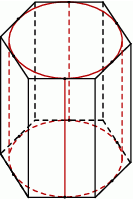
Rozpatrujemy wszystkie graniastosłupy prawidłowe sześciokątne takie, że suma długości promienia i wysokości walca wpisanego w ten graniastosłup jest równa 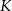 . Oblicz pole powierzchni całkowitej tego z rozważanych graniastosłupów, którego objętość jest największa.
. Oblicz pole powierzchni całkowitej tego z rozważanych graniastosłupów, którego objętość jest największa.
Krawędź podstawy ostrosłupa trójkątnego prawidłowego jest równa 6. Jego objętość jest równa 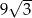 . Wyznacz długość wysokości ściany bocznej ostrosłupa.
. Wyznacz długość wysokości ściany bocznej ostrosłupa.
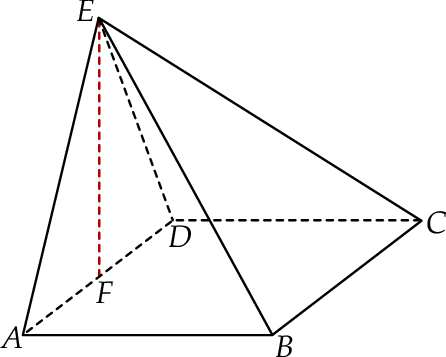
Podstawą ostrosłupa 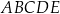 jest kwadrat o boku długości 12. Spodek
jest kwadrat o boku długości 12. Spodek 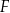 wysokości
wysokości 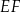 ostrosłupa jest środkiem krawędzi
ostrosłupa jest środkiem krawędzi 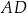 . Wiedząc, że dwie krótsze krawędzie boczne mają tę samą długość, równą 10, oblicz tangens kąta nachylenia krawędzi
. Wiedząc, że dwie krótsze krawędzie boczne mają tę samą długość, równą 10, oblicz tangens kąta nachylenia krawędzi 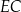 do płaszczyzny podstawy.
do płaszczyzny podstawy.
Środki ścian czworościanu foremnego  są wierzchołkami czworościanu
są wierzchołkami czworościanu 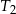 . Oblicz stosunek objętości czworościanów
. Oblicz stosunek objętości czworościanów 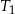 i
i 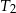 .
.
Dany jest ostrosłup prawidłowy czworokątny o krawędzi podstawy 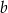 i kącie nachylenia krawędzi bocznej do krawędzi podstawy
i kącie nachylenia krawędzi bocznej do krawędzi podstawy  . Oblicz pole przekroju płaszczyzną przechodzącą przez wierzchołek i równoległą do krawędzi podstawy oraz nachyloną do płaszczyzny podstawy pod kątem
. Oblicz pole przekroju płaszczyzną przechodzącą przez wierzchołek i równoległą do krawędzi podstawy oraz nachyloną do płaszczyzny podstawy pod kątem 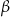 . Podaj konieczne założenia dotyczące kąta
. Podaj konieczne założenia dotyczące kąta  .
.
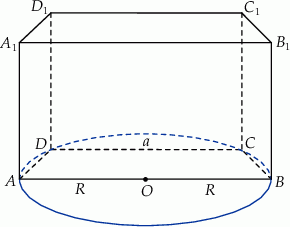
Podstawą graniastosłupa prostego  jest trapez równoramienny
jest trapez równoramienny  wpisany w okrąg o środku
wpisany w okrąg o środku  i promieniu
i promieniu 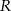 . Dłuższa podstawa
. Dłuższa podstawa 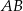 trapezu jest średnicą tego okręgu, a krótsza ma długość
trapezu jest średnicą tego okręgu, a krótsza ma długość  (zobacz rysunek). Przekątna graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem o mierze
(zobacz rysunek). Przekątna graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem o mierze  . Wyznacz objętość tego graniastosłupa jako funkcję promienia
. Wyznacz objętość tego graniastosłupa jako funkcję promienia 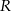 , długości podstawy
, długości podstawy  i miary kąta
i miary kąta  .
.
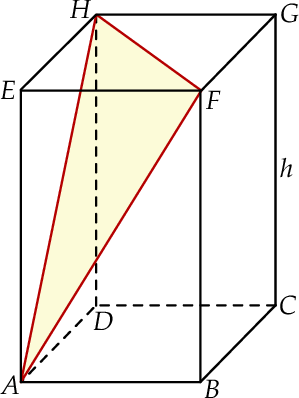
Dany jest graniastosłup prosty 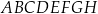 o podstawie prostokątnej
o podstawie prostokątnej 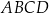 . Przekątne
. Przekątne 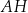 ,
, 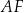 i
i 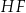 ścian bocznych tworzą trójkąt ostrokątny o polu 11,25 (zobacz rysunek). Stosunek długości odcinka
ścian bocznych tworzą trójkąt ostrokątny o polu 11,25 (zobacz rysunek). Stosunek długości odcinka 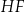 do promienia okręgu opisanego na trójkącie
do promienia okręgu opisanego na trójkącie 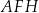 jest równy 30 : 17. Oblicz wysokość
jest równy 30 : 17. Oblicz wysokość 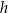 tego graniastosłupa.
tego graniastosłupa.