Trójkąt 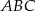 jest podstawą ostrosłupa
jest podstawą ostrosłupa 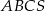 . Punkt
. Punkt 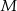 jest środkiem boku
jest środkiem boku 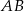 i
i 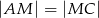 . Odcinek
. Odcinek 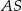 jest wysokością tego ostrosłupa. Wykaż, że kąt
jest wysokością tego ostrosłupa. Wykaż, że kąt 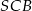 jest prosty.
jest prosty.
/Szkoła średnia/Geometria/Stereometria
Dach wieży ma kształt powierzchni bocznej ostrosłupa prawidłowego czworokątnego, którego krawędź podstawy ma długość 4 m. Ściana boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem 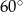 .
.
- Sporządź pomocniczy rysunek i zaznacz na nim podane w zadaniu wielkości.
- Oblicz, ile sztuk dachówek należy kupić, aby pokryć ten dach, wiedząc, że do pokrycia
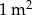 potrzebne są 24 dachówki. Przy zakupie należy doliczyć 8% dachówek na zapas.
potrzebne są 24 dachówki. Przy zakupie należy doliczyć 8% dachówek na zapas.
Rozpatrujemy wszystkie walce, których przekrojem osiowym jest prostokąt, w którym suma długości przekątnej i jednego boku jest równa 10. Oblicz wysokość i promień podstawy tego walca, którego objętość jest największa. Oblicz objętość tego walca.
Rozważamy wszystkie ostrosłupy prawidłowe trójkątne, w których suma długości wszystkich krawędzi jest równa 6.
-
Wyznacz zależność objętości
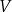 ostrosłupa od jego krawędzi podstawy
ostrosłupa od jego krawędzi podstawy  i podaj dziedzinę funkcji
i podaj dziedzinę funkcji 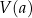 .
. -
Wyznacz długość krawędzi podstawy tego z rozważanych ostrosłupów, którego objętość jest największa. Oblicz tą największą objętość.
W trójkącie ostrokątnym 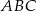 mamy
mamy 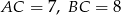 , zaś
, zaś 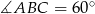 . Oblicz objętość bryły powstałej z obrotu trójkąta
. Oblicz objętość bryły powstałej z obrotu trójkąta 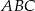 wokół prostej zawierającej bok
wokół prostej zawierającej bok 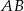 .
.
Krawędź podstawy ostrosłupa prawidłowego czworokątnego 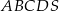 ma długość
ma długość  . Ściana boczna jest nachylona do płaszczyzny podstawy ostrosłupa pod kątem
. Ściana boczna jest nachylona do płaszczyzny podstawy ostrosłupa pod kątem 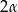 . Ostrosłup ten przecięto płaszczyzną, która przechodzi przez krawędź podstawy i dzieli na połowy kąt pomiędzy ścianą boczną i podstawą. Oblicz pole powstałego przekroju tego ostrosłupa.
. Ostrosłup ten przecięto płaszczyzną, która przechodzi przez krawędź podstawy i dzieli na połowy kąt pomiędzy ścianą boczną i podstawą. Oblicz pole powstałego przekroju tego ostrosłupa.
Oblicz objętość ostrosłupa prawidłowego czworokątnego o krawędzi podstawy 2 dm i krawędzi bocznej 4 dm.
Oblicz objętość ostrosłupa prawidłowego czworokątnego o krawędzi podstawy 4 dm i krawędzi bocznej 6 dm.
Podstawą ostrosłupa 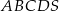 jest prostokąt, którego boki pozostają w stosunku 3:4, a pole jest równe 192 (zobacz rysunek). Punkt
jest prostokąt, którego boki pozostają w stosunku 3:4, a pole jest równe 192 (zobacz rysunek). Punkt 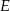 jest wyznaczony przez przecinające się przekątne podstawy, a odcinek
jest wyznaczony przez przecinające się przekątne podstawy, a odcinek 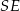 jest wysokością ostrosłupa. Każda krawędź boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem
jest wysokością ostrosłupa. Każda krawędź boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem 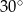 . Oblicz objętość ostrosłupa.
. Oblicz objętość ostrosłupa.
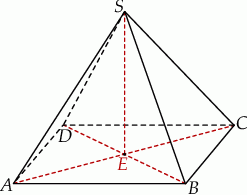
Podstawą ostrosłupa 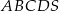 jest prostokąt, którego boki pozostają w stosunku 5:12, a pole jest równe 240 (zobacz rysunek). Punkt
jest prostokąt, którego boki pozostają w stosunku 5:12, a pole jest równe 240 (zobacz rysunek). Punkt 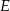 jest wyznaczony przez przecinające się przekątne podstawy, a odcinek
jest wyznaczony przez przecinające się przekątne podstawy, a odcinek 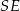 jest wysokością ostrosłupa. Każda krawędź boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem
jest wysokością ostrosłupa. Każda krawędź boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem 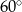 . Oblicz objętość ostrosłupa.
. Oblicz objętość ostrosłupa.
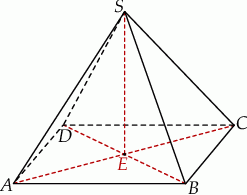
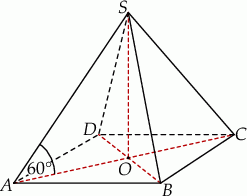
Podstawą ostrosłupa 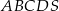 jest prostokąt o polu równym 432, a stosunek długości boków tego prostokąta jest równy 3:4. Przekątne podstawy
jest prostokąt o polu równym 432, a stosunek długości boków tego prostokąta jest równy 3:4. Przekątne podstawy 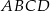 przecinają się w punkcie
przecinają się w punkcie 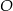 . Odcinek
. Odcinek 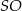 jest wysokością ostrosłupa (zobacz rysunek). Kąt
jest wysokością ostrosłupa (zobacz rysunek). Kąt 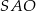 ma miarę
ma miarę 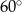 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
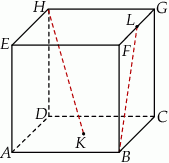
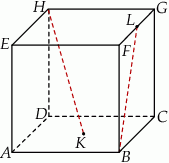
W narysowanym obok sześcianie krawędź ma długość  . Oblicz odległość wierzchołka
. Oblicz odległość wierzchołka  od płaszczyzny przechodzącej przez wierzchołki
od płaszczyzny przechodzącej przez wierzchołki 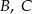 i
i  .
.
W ostrosłupie prawidłowym czworokątnym 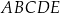 punkt
punkt 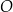 jest środkiem symetrii podstawy ostrosłupa. Stosunek obwodu podstawy
jest środkiem symetrii podstawy ostrosłupa. Stosunek obwodu podstawy 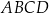 do sumy długości wszystkich krawędzi ostrosłupa jest równy 1:5. Przez przekątną
do sumy długości wszystkich krawędzi ostrosłupa jest równy 1:5. Przez przekątną 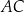 podstawy i środek
podstawy i środek 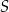 krawędzi bocznej
krawędzi bocznej 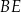 poprowadzono płaszczyznę. Oblicz stosunek pola otrzymanego przekroju do pola podstawy ostrosłupa oraz miarę kąta
poprowadzono płaszczyznę. Oblicz stosunek pola otrzymanego przekroju do pola podstawy ostrosłupa oraz miarę kąta 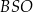 (w zaokrągleniu do
(w zaokrągleniu do 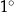 ).
).
Oblicz promień kuli stycznej do wszystkich krawędzi czworościanu foremnego o krawędzi długości  .
.
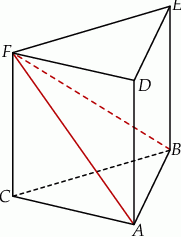
Dany jest graniastosłup prawidłowy trójkątny 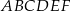 o podstawach
o podstawach 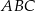 i
i 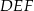 i krawędziach bocznych
i krawędziach bocznych 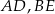 i
i 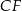 (zobacz rysunek). Krawędzie boczne graniastosłupa mają długość 8, a tangens kąta między wysokością trójkąta
(zobacz rysunek). Krawędzie boczne graniastosłupa mają długość 8, a tangens kąta między wysokością trójkąta 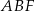 poprowadzoną z wierzchołka
poprowadzoną z wierzchołka 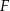 i płaszczyzną podstawy
i płaszczyzną podstawy 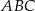 tego graniastosłupa jest równy
tego graniastosłupa jest równy 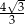 . Oblicz pole trójkąta
. Oblicz pole trójkąta 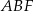 .
.
Podstawą ostrosłupa  jest prostokąt
jest prostokąt  , którego boki mają długości
, którego boki mają długości 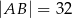 i
i 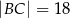 . Ściany boczne
. Ściany boczne 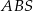 i
i 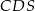 są trójkątami przystającymi i każda z nich jest nachylona do płaszczyzny podstawy ostrosłupa pod kątem
są trójkątami przystającymi i każda z nich jest nachylona do płaszczyzny podstawy ostrosłupa pod kątem  . Ściany boczne
. Ściany boczne 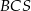 i
i 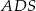 są trójkątami przystającymi i każda z nich jest nachylona do płaszczyzny podstawy pod kątem
są trójkątami przystającymi i każda z nich jest nachylona do płaszczyzny podstawy pod kątem 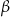 . Miary kątów
. Miary kątów  i
i 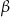 spełniają warunek:
spełniają warunek: 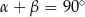 . Oblicz
. Oblicz 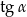 oraz pole powierzchni całkowitej tego ostrosłupa.
oraz pole powierzchni całkowitej tego ostrosłupa.
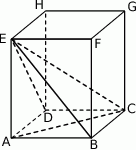
W graniastosłupie prawidłowym czworokątnym 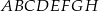 przekątna
przekątna 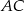 podstawy ma długość 4. Kąt
podstawy ma długość 4. Kąt 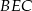 jest równy
jest równy 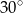 . Oblicz objętość ostrosłupa
. Oblicz objętość ostrosłupa 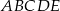 przedstawionego na poniższym rysunku.
przedstawionego na poniższym rysunku.
Pewien zakład otrzymał zamówienie na wykonanie prostopadłościennego zbiornika (całkowicie otwartego od góry) o pojemności 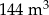 . Dno zbiornika ma być kwadratem. Żaden z wymiarów zbiornika (krawędzi prostopadłościanu) nie może przekraczać 9 metrów. Całkowity koszt wykonania zbiornika ustalono w następujący sposób:
. Dno zbiornika ma być kwadratem. Żaden z wymiarów zbiornika (krawędzi prostopadłościanu) nie może przekraczać 9 metrów. Całkowity koszt wykonania zbiornika ustalono w następujący sposób:
– 100 zł za 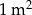 dna
dna
– 75 zł za 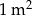 ściany bocznej.
ściany bocznej.
Oblicz wymiary zbiornika, dla którego tak ustalony koszt wykonania będzie najmniejszy.
Zakład produkcyjny dostał zlecenie produkcji prostopadłościennych pudełek (całkowicie otwartych od góry) o objętości 60,75 litra. Dno pudełka ma być kwadratem i żaden z jego wymiarów nie może przekraczać 67,5 cm. Na koszt wykonania pudełka składają się – koszt wykonania 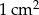 dna w wysokości 48 gorszy oraz koszt wykonania
dna w wysokości 48 gorszy oraz koszt wykonania 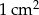 ściany bocznej w wysokości 36 groszy. Oblicz wymiary pudełka, dla których koszt jego produkcji będzie najmniejszy.
ściany bocznej w wysokości 36 groszy. Oblicz wymiary pudełka, dla których koszt jego produkcji będzie najmniejszy.
Punkty 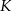 i
i 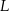 są środkami odpowiednio podstawy
są środkami odpowiednio podstawy 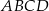 i krawędzi
i krawędzi 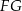 sześcianu
sześcianu 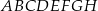 . Suma kwadratów długości odcinków
. Suma kwadratów długości odcinków 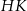 i
i 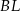 jest równa 33. Oblicz pole powierzchni całkowitej sześcianu.
jest równa 33. Oblicz pole powierzchni całkowitej sześcianu.
Punkty  i
i  są środkami odpowiednio podstawy
są środkami odpowiednio podstawy  i krawędzi
i krawędzi 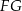 sześcianu
sześcianu 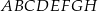 . Suma kwadratów długości odcinków
. Suma kwadratów długości odcinków 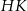 i
i 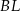 jest równa 44. Oblicz objętość tego sześcianu.
jest równa 44. Oblicz objętość tego sześcianu.
Graniastosłup prawidłowy trójkątny przecięto płaszczyzną, przechodzącą przez środek ciężkości górnej podstawy i krawędź dolnej podstawy, pod kątem 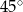 do dolnej podstawy. Pole otrzymanego przekroju wynosi
do dolnej podstawy. Pole otrzymanego przekroju wynosi 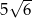 . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa.
Rozważamy wszystkie prostopadłościany  , w których krawędź
, w których krawędź 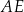 jest 3 razy dłuższa od krawędzi
jest 3 razy dłuższa od krawędzi 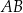 , a suma długości wszystkich dwunastu krawędzi prostopadłościanu jest równa 48 (zobacz rysunek).
, a suma długości wszystkich dwunastu krawędzi prostopadłościanu jest równa 48 (zobacz rysunek).
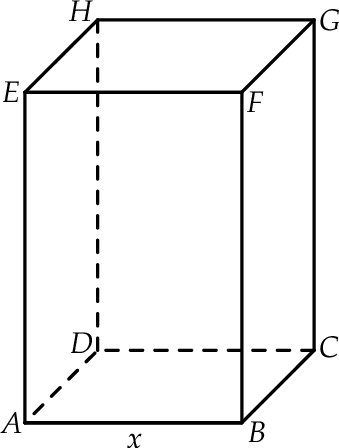
Niech 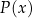 oznacza funkcję pola powierzchni całkowitej takiego prostopadłościanu w zależności od długości
oznacza funkcję pola powierzchni całkowitej takiego prostopadłościanu w zależności od długości  krawędzi
krawędzi 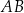 .
.
-
Wyznacz wzór i dziedzinę funkcji
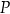 .
. -
Oblicz długość
 krawędzi
krawędzi 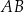 tego z rozważanych prostopadłościanów, którego pole powierzchni całkowitej jest największe.
tego z rozważanych prostopadłościanów, którego pole powierzchni całkowitej jest największe.
Stożek, którego pole powierzchni bocznej jest równe 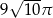 , jest wpisany w kulę o promieniu 5. Oblicz objętość stożka.
, jest wpisany w kulę o promieniu 5. Oblicz objętość stożka.
Dany jest ostrosłup prawidłowy czworokątny o podstawie 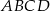 i wierzchołku
i wierzchołku 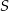 . Pole trójkąta
. Pole trójkąta 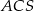 jest równe
jest równe 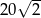 , krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem, którego tangens jest równy
, krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem, którego tangens jest równy 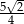 . Oblicz objętość ostrosłupa.
. Oblicz objętość ostrosłupa.

