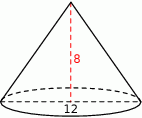
Przekrój osiowy stożka jest trójkątem równoramiennym o podstawie długości 12. Wysokość stożka jest równa 8. Oblicz pole powierzchni bocznej tego stożka.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Przekrój osiowy stożka jest trójkątem równoramiennym o podstawie długości 12. Wysokość stożka jest równa 8. Oblicz pole powierzchni bocznej tego stożka.

Podstawą ostrosłupa prawidłowego jest trójkąt równoboczny. Wysokość ściany bocznej tego ostrosłupa jest równa 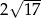 , a tangens kąta nachylenia ściany bocznej ostrosłupa do płaszczyzny jego podstawy jest równy 4. Oblicz objętość tego ostrosłupa.
, a tangens kąta nachylenia ściany bocznej ostrosłupa do płaszczyzny jego podstawy jest równy 4. Oblicz objętość tego ostrosłupa.
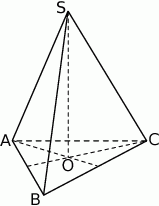
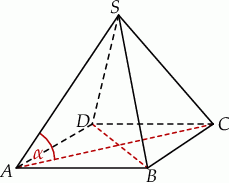
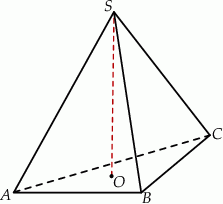
Podstawą ostrosłupa 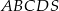 jest romb o boku długości 6. Krawędź boczna
jest romb o boku długości 6. Krawędź boczna 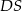 ma długość 8 i jest jednocześnie wysokością tego ostrosłupa. Długości pozostałych trzech krawędzi bocznych są równe (zobacz rysunek).
ma długość 8 i jest jednocześnie wysokością tego ostrosłupa. Długości pozostałych trzech krawędzi bocznych są równe (zobacz rysunek).
Oblicz objętość tego ostrosłupa.
Rozpatrujemy wszystkie prostopadłościany o objętości 8, których stosunek długości dwóch krawędzi wychodzących z tego samego wierzchołka jest równy 1:2 oraz suma długości wszystkich dwunastu krawędzi jest mniejsza od 28. Wyznacz pole powierzchni całkowitej prostopadłościanu jako funkcję długości jednej z jego krawędzi. Wyznacz dziedzinę tej funkcji. Oblicz wymiary tego spośród rozpatrywanych prostopadłościanów, którego pole powierzchni całkowitej jest najmniejsze.
Rozpatrujemy wszystkie prostopadłościany o objętości 27, których stosunek długości dwóch krawędzi wychodzących z tego samego wierzchołka jest równy 1:3 oraz suma długości wszystkich dwunastu krawędzi jest mniejsza od 52. Wyznacz pole powierzchni całkowitej prostopadłościanu jako funkcję długości jednej z jego krawędzi. Wyznacz dziedzinę tej funkcji. Oblicz wymiary tego spośród rozpatrywanych prostopadłościanów, którego pole powierzchni całkowitej jest najmniejsze.
W graniastosłupie prawidłowym czworokątnym przekątne ścian bocznych, wychodzące z tego samego wierzchołka, mają długość 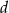 i tworzą kąt o mierze
i tworzą kąt o mierze  . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa.
Przekątna sześcianu ma długość 6. Oblicz objętość tego sześcianu.
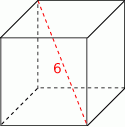
Sześcian przecięto płaszczyzną przechodzącą przez przekątną podstawy. Płaszczyzna ta tworzy z podstawą kąt  . Dla jakich wartości
. Dla jakich wartości 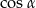 otrzymany przekrój jest trójkątem?
otrzymany przekrój jest trójkątem?
Pole podstawy stożka jest równe 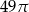 , a jego pole powierzchni bocznej jest równe
, a jego pole powierzchni bocznej jest równe 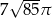 . Oblicz objętość tego stożka.
. Oblicz objętość tego stożka.
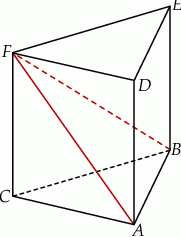
Dany jest graniastosłup prawidłowy trójkątny 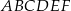 o podstawach
o podstawach 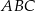 i
i 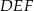 i krawędziach bocznych
i krawędziach bocznych 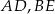 i
i 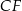 (zobacz rysunek). Długość krawędzi podstawy
(zobacz rysunek). Długość krawędzi podstawy 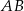 jest równa 8, a pole trójkąta
jest równa 8, a pole trójkąta 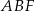 jest równe 52. Oblicz objętość tego graniastosłupa.
jest równe 52. Oblicz objętość tego graniastosłupa.
Podstawą prostopadłościanu 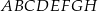 o wysokości 4 jest kwadrat
o wysokości 4 jest kwadrat 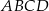 o boku 3. Oblicz sinus kąta, pod którym przecinają się przekątne
o boku 3. Oblicz sinus kąta, pod którym przecinają się przekątne 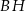 i
i 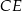 tego prostopadłościanu.
tego prostopadłościanu.
Powierzchnia boczna walca po rozwinięciu na płaszczyznę jest prostokątem. Przekątna tego prostokąta ma długość 12 i tworzy z bokiem, którego długość jest równa wysokości walca, kąt o mierze 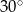 .
.
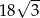 . Odpowiedź uzasadnij.
. Odpowiedź uzasadnij.Kąt  jest kątem nachylenia krawędzi bocznej ostrosłupa prawidłowego czworokątnego do płaszczyzny podstawy (zobacz rysunek). Oblicz stosunek pola powierzchni całkowitej tego ostrosłupa do pola jego podstawy, jeżeli
jest kątem nachylenia krawędzi bocznej ostrosłupa prawidłowego czworokątnego do płaszczyzny podstawy (zobacz rysunek). Oblicz stosunek pola powierzchni całkowitej tego ostrosłupa do pola jego podstawy, jeżeli 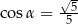 .
.
Objętość graniastosłupa prawidłowego czworokątnego jest równa 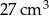 , Pole powierzchni całkowitej graniastosłupa jest funkcją długości jego krawędzi podstawy. Napisz wzór tej funkcji i wyznacz jej przedziały monotoniczności.
, Pole powierzchni całkowitej graniastosłupa jest funkcją długości jego krawędzi podstawy. Napisz wzór tej funkcji i wyznacz jej przedziały monotoniczności.
W ostrosłupie prawidłowym trójkątnym stosunek pola powierzchni bocznej do pola podstawy jest równe 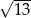 . Oblicz miarę kąta nachylenia krawędzi bocznej tego ostrosłupa do płaszczyzny podstawy.
. Oblicz miarę kąta nachylenia krawędzi bocznej tego ostrosłupa do płaszczyzny podstawy.
W ostrosłupie prawidłowym trójkątnym 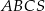 krawędź podstawy ma długość
krawędź podstawy ma długość  . Pole powierzchni bocznej tego ostrosłupa jest dwa razy większe od pola jego podstawy. Oblicz cosinus kąta nachylenia krawędzi bocznej tego ostrosłupa do płaszczyzny jego podstawy.
. Pole powierzchni bocznej tego ostrosłupa jest dwa razy większe od pola jego podstawy. Oblicz cosinus kąta nachylenia krawędzi bocznej tego ostrosłupa do płaszczyzny jego podstawy.
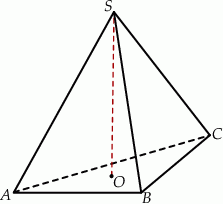
W ostrosłupie prawidłowym trójkątnym 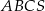 pole powierzchni bocznej jest trzy razy większe od pola podstawy. Oblicz sinus kąta nachylenia ściany bocznej tego ostrosłupa do płaszczyzny jego podstawy.
pole powierzchni bocznej jest trzy razy większe od pola podstawy. Oblicz sinus kąta nachylenia ściany bocznej tego ostrosłupa do płaszczyzny jego podstawy.
Podstawą ostrosłupa 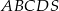 jest prostokąt
jest prostokąt 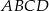 , a krawędź boczna
, a krawędź boczna 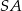 jest jego wysokością. Wykaż, że suma kwadratów pól ścian
jest jego wysokością. Wykaż, że suma kwadratów pól ścian 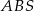 i
i 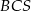 jest równa sumie kwadratów pól ścian
jest równa sumie kwadratów pól ścian 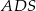 i
i 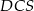 .
.
Dany jest ostrosłup prawidłowy czworokątny o wysokości 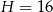 . Suma długości wszystkich jego krawędzi jest równa
. Suma długości wszystkich jego krawędzi jest równa 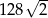 . Oblicz cosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy tego ostrosłupa.
. Oblicz cosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy tego ostrosłupa.
Punkty 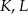 i
i 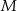 są środkami krawędzi
są środkami krawędzi 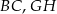 i
i 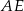 sześcianu
sześcianu 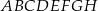 o krawędzi długości 1 (zobacz rysunek). Oblicz pole trójkąta
o krawędzi długości 1 (zobacz rysunek). Oblicz pole trójkąta 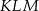 .
.
Punkty 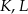 i
i 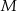 są środkami krawędzi
są środkami krawędzi 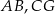 i
i 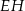 sześcianu
sześcianu 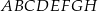 o krawędzi długości 1 (zobacz rysunek). Oblicz pole trójkąta
o krawędzi długości 1 (zobacz rysunek). Oblicz pole trójkąta 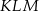 .
.
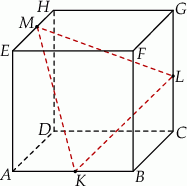
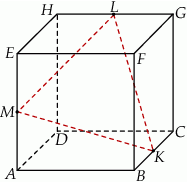
Na krawędziach sześcianu 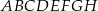 zaznaczono punkty
zaznaczono punkty 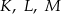 tak, że każdy z nich jest środkiem odpowiedniej krawędzi (patrz rysunek). Oblicz pole trójkąta
tak, że każdy z nich jest środkiem odpowiedniej krawędzi (patrz rysunek). Oblicz pole trójkąta 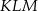 , jeśli krawędź sześcianu ma długość równą 4.
, jeśli krawędź sześcianu ma długość równą 4.
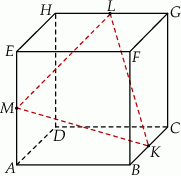
Na krawędziach sześcianu 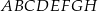 zaznaczono punkty
zaznaczono punkty 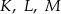 tak, że każdy z nich jest środkiem odpowiedniej krawędzi (patrz rysunek). Oblicz pole trójkąta
tak, że każdy z nich jest środkiem odpowiedniej krawędzi (patrz rysunek). Oblicz pole trójkąta 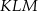 , jeśli krawędź sześcianu ma długość równą 2.
, jeśli krawędź sześcianu ma długość równą 2.
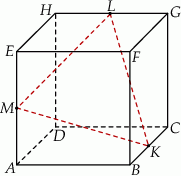
Oblicz sinus kąta między przekątną sześcianu a jego płaszczyzną podstawy.
Podstawą graniastosłupa prostego jest trójkąt 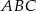 o bokach mających długość 5,7,8. Oblicz cosinusy kątów, jakie tworzą dwie kolejne ściany boczne tego graniastosłupa.
o bokach mających długość 5,7,8. Oblicz cosinusy kątów, jakie tworzą dwie kolejne ściany boczne tego graniastosłupa.
Trójkąt 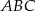 jest podstawą ostrosłupa
jest podstawą ostrosłupa 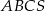 . Punkt
. Punkt 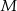 jest środkiem boku
jest środkiem boku 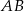 i
i 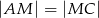 . Odcinek
. Odcinek 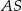 jest wysokością tego ostrosłupa. Wykaż, że kąt
jest wysokością tego ostrosłupa. Wykaż, że kąt 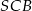 jest prosty.
jest prosty.
