Długość promienia walca zmniejszono dziesięciokrotnie. Ile razy trzeba zwiększyć wysokość tego walca aby objętość się nie zmieniła?
/Szkoła średnia/Geometria/Stereometria
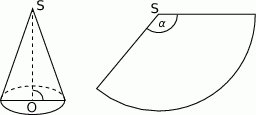
Powierzchnia boczna stożka po rozwinięciu na płaszczyznę jest wycinkiem koła o promieniu 3 i kącie środkowym 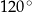 (zobacz rysunek). Oblicz objętość tego stożka.
(zobacz rysunek). Oblicz objętość tego stożka.

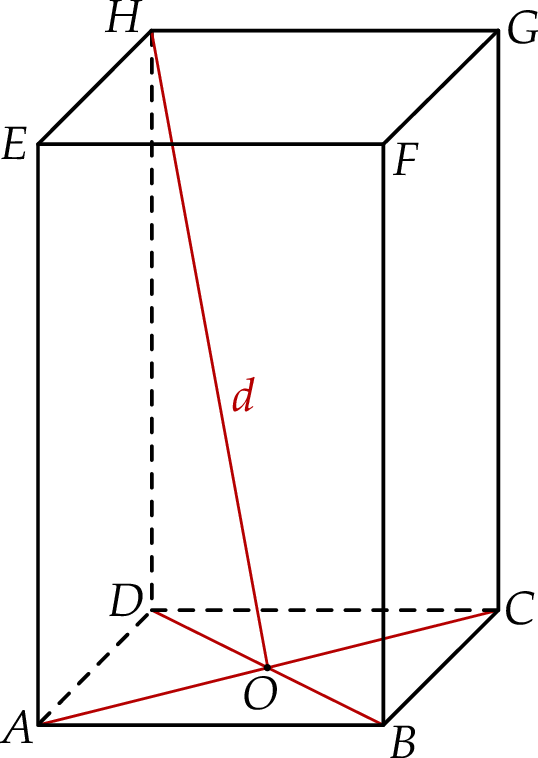
Rozważamy wszystkie graniastosłupy prawidłowe czworokątne 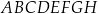 , w których odcinek łączący punkt
, w których odcinek łączący punkt 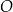 przecięcia przekątnych
przecięcia przekątnych 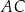 i
i 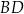 podstawy
podstawy 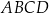 z dowolnym wierzchołkiem podstawy
z dowolnym wierzchołkiem podstawy 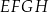 ma długość
ma długość 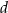 (zobacz rysunek).
(zobacz rysunek).
-
Wyznacz zależność objętości
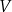 graniastosłupa od jego wysokości
graniastosłupa od jego wysokości 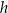 i podaj dziedzinę funkcji
i podaj dziedzinę funkcji 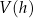 .
. -
Wyznacz wysokość tego z rozważanych graniastosłupów, którego objętość jest największa.
Rozważamy wszystkie graniastosłupy prawidłowe czworokątne 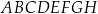 , w których odcinek łączący punkt
, w których odcinek łączący punkt 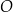 przecięcia przekątnych
przecięcia przekątnych 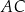 i
i 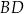 podstawy
podstawy  z dowolnym wierzchołkiem podstawy
z dowolnym wierzchołkiem podstawy  ma długość 3 (zobacz rysunek).
ma długość 3 (zobacz rysunek).
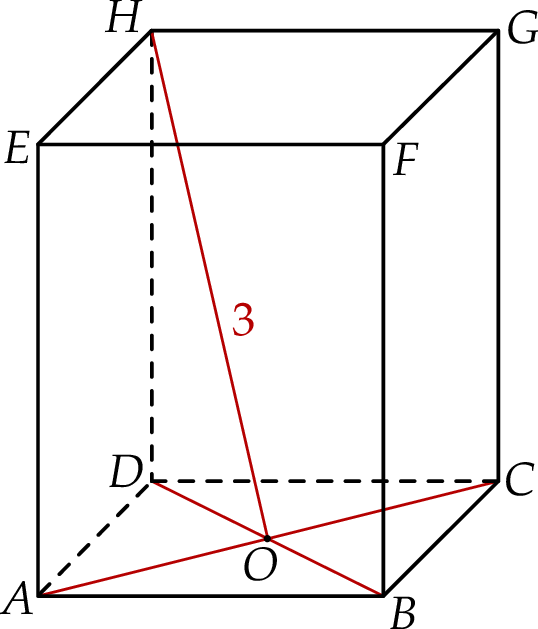
Wyznacz wymiary tego z rozważanych graniastosłupów, którego objętość jest największa. Oblicz tę największą objętość.
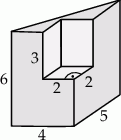
Bryła przedstawiona na poniższym rysunku powstała przez wycięcie z graniastosłupa prostego trójkątnego innego graniastosłupa prostego. Oblicz pole powierzchni i objętość tej bryły.
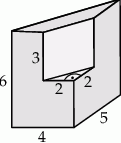
Bryła przedstawiona na poniższym rysunku powstała przez wycięcie z graniastosłupa prostego trójkątnego innego graniastosłupa prostego. Oblicz pole powierzchni i objętość tej bryły.
Dwie kule mające średnice 4 cm i 1 cm wpisano w stożek w ten sposób, że większa jest styczna do podstawy i powierzchni bocznej stożka, zaś mniejsza – do powierzchni bocznej stożka i do większej kuli. Oblicz pole powierzchni tego stożka.
Objętość stożka jest równa 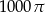 , a tworząca jest nachylona do podstawy pod kątem
, a tworząca jest nachylona do podstawy pod kątem 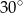 . Oblicz pole powierzchni bocznej tego stożka.
. Oblicz pole powierzchni bocznej tego stożka.
Objętość stożka jest równa 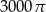 , a tworząca jest nachylona do podstawy pod kątem
, a tworząca jest nachylona do podstawy pod kątem 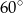 . Oblicz pole powierzchni bocznej tego stożka.
. Oblicz pole powierzchni bocznej tego stożka.
Krawędź sześcianu jest o 4 krótsza od jego przekątnej. Oblicz pole powierzchni całkowitej tego sześcianu.
Pole powierzchni całkowitej stożka jest trzy razy większe od pola jego podstawy. Oblicz stosunek objętości stożka do objętości wpisanej w niego kuli.
Pole podstawy stożka jest trzy razy mniejsze od jego pola powierzchni całkowitej. Oblicz stosunek objętości kuli wpisanej w stożek do objętości stożka.
Czworościan foremny przecięto płaszczyzną 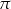 styczną do kuli wpisanej w ten czworościan (tzn. kuli stycznej do wszystkich ścian czworościanu) oraz równoległą do jednej ze ścian czworościanu. Oblicz stosunek objętości brył, na które płaszczyzna
styczną do kuli wpisanej w ten czworościan (tzn. kuli stycznej do wszystkich ścian czworościanu) oraz równoległą do jednej ze ścian czworościanu. Oblicz stosunek objętości brył, na które płaszczyzna 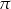 podzieliła czworościan.
podzieliła czworościan.
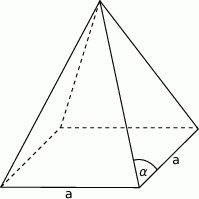
W ostrosłupie prawidłowym czworokątnym krawędź podstawy ma długość  . Kąt między krawędzią boczną, a krawędzią podstawy ma miarę
. Kąt między krawędzią boczną, a krawędzią podstawy ma miarę 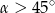 (zobacz rysunek). Oblicz objętość tego ostrosłupa.
(zobacz rysunek). Oblicz objętość tego ostrosłupa.
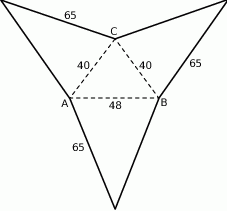
Oblicz objętość ostrosłupa trójkątnego 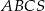 , którego siatkę przedstawiono na rysunku.
, którego siatkę przedstawiono na rysunku.
W ostrosłupie prawidłowym czworokątnym krawędź boczna ma długość 4 cm i jest nachylona do płaszczyzny podstawy pod kątem  . Oblicz objętość ostrosłupa.
. Oblicz objętość ostrosłupa.
Podstawą ostrosłupa jest trójkąt o danych kątach  i
i 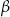 . Wszystkie krawędzie boczne mają długość
. Wszystkie krawędzie boczne mają długość 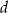 i są nachylone do płaszczyzny podstawy pod kątem o mierze
i są nachylone do płaszczyzny podstawy pod kątem o mierze 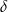 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Rozwinięcie powierzchni bocznej stożka jest wycinkiem kołowym o kącie środkowym  . Kąt ten oparty jest na cięciwie o długości
. Kąt ten oparty jest na cięciwie o długości  . Oblicz objętość stożka.
. Oblicz objętość stożka.
Tworząca stożka ma długość 3 dm. Długość promienia podstawy stożka jest równa 1 dm. Powierzchnia boczna stożka po rozwinięciu na płaszczyznę jest wycinkiem koła. Oblicz miarę  kąta środkowego tego wycinka.
kąta środkowego tego wycinka.
Trapez równoramienny o podstawach długości 14 cm i 26 cm oraz o wysokości 6 cm obraca się wokół swojej osi symetrii. Oblicz objętość otrzymanej bryły.
Firma logistyczna planuje produkcję pojemników w kształcie graniastosłupa prostego o objętości 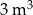 i podstawie będącej prostokątem, w którym jeden z boków jest 4 razy dłuższy od drugiego. Koszt materiału potrzebnego do produkcji ścian bocznych tego pojemnika wynosi 40 zł za
i podstawie będącej prostokątem, w którym jeden z boków jest 4 razy dłuższy od drugiego. Koszt materiału potrzebnego do produkcji ścian bocznych tego pojemnika wynosi 40 zł za 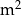 , a koszt materiału potrzebnego do produkcji jego górnej i dolnej podstawy wynosi 60 zł za
, a koszt materiału potrzebnego do produkcji jego górnej i dolnej podstawy wynosi 60 zł za 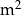 . Oblicz jakie powinny być wymiary tego pojemnika, aby koszt jego produkcji był najmniejszy możliwy.
. Oblicz jakie powinny być wymiary tego pojemnika, aby koszt jego produkcji był najmniejszy możliwy.
Tworząca stożka ma długość 17, a wysokość stożka jest krótsza od średnicy jego podstawy o 22. Oblicz pole powierzchni całkowitej i objętość tego stożka.
Tworząca stożka ma długość 25, a średnica podstawy stożka jest krótsza od wysokości stożka o 10. Oblicz pole powierzchni całkowitej i objętość tego stożka.
Pole powierzchni bocznej ostrosłupa prawidłowego trójkątnego jest równe 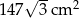 , a pole jego powierzchni całkowitej wynosi
, a pole jego powierzchni całkowitej wynosi 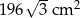 . Oblicz długość krawędzi podstawy i długość krawędzi bocznej tego ostrosłupa.
. Oblicz długość krawędzi podstawy i długość krawędzi bocznej tego ostrosłupa.
Wysokość ostrosłupa prawidłowego czworokątnego jest równa 8. Krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem  takim, że
takim, że 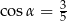 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.

