Stereometria/Geometria/Szkoła średnia - zadania z matematyki

/Szkoła średnia/Geometria/Stereometria

Tworząca stożka ma długość 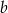. Wyznacz wysokość tego stożka, którego objętość jest największa. Oblicz objętość tego stożka.

Oblicz objętość stożka wpisanego w kulę o promieniu 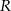, wiedząc, że kąt rozwarcia stożka ma miarę .

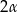Krawędź boczna ostrosłupa prawidłowego trójkątnego ma długość 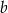i tworzy z płaszczyzną podstawy kąt o mierze . Jaką objętość ma ten ostrosłup?

Podstawą prostopadłościanu jest kwadrat. Przekątna tego prostopadłościanu ma długość 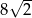√ -- 8 2 i jest nachylona do płaszczyzny podstawy pod kątem 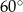60 ∘ . Oblicz objętość i pole powierzchni całkowitej prostopadłościanu i wykonaj rysunek.

Ukryj Podobne zadania

Przekątna prostopadłościanu ma długość 24 i tworzy z płaszczyzną jego podstawy kąt 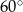60∘ . Jedna z krawędzi podstawy ma długość 8. Wyznacz objętość i pole powierzchni całkowitej tego prostopadłościanu.

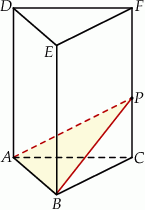
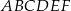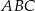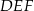Dany jest graniastosłup prawidłowy trójkątny ABCDEF o podstawach ABC i DEF i krawędziach bocznych 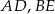AD ,BE i 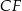(zobacz rysunek). Przez krawędź 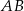poprowadzono płaszczyznę nachyloną do płaszczyzny podstawy pod kątem 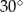30∘ . Płaszczyzna ta przecina krawędź 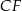w punkcie 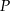. Oblicz pole trójkąta 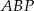ABP jeżeli objętość ostrosłupa 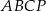ABCP jest równa √ -- 9 3 .

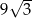Przekątna prostopadłościanu ma długość 8 cm, a miara kąta, jaki tworzy ona ze ścianą boczną wynosi 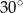30∘ . Oblicz objętość prostopadłościanu, jeśli jego wysokość wynosi √ -- 2 7 cm .

Ukryj Podobne zadania

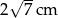Przekątna prostopadłościanu ma długość 12 cm, a miara kąta, jaki tworzy ona ze ścianą boczną wynosi 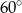60∘ . Oblicz objętość prostopadłościanu, jeśli jego wysokość wynosi √ -- 2 5 cm .

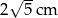W kulę wpisano walec w ten sposób, że objętość walca stanowi 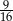-9 16 objętości kuli. Oblicz stosunek promienia kuli do wysokości walca.

W ostrosłupie prawidłowym trójkątnym krawędź podstawy ma długość 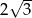√ -- 2 3 . Oblicz objętość tego ostrosłupa jeżeli kąt nachylenia krawędzi bocznej do podstawy ma miarę 60∘ .

Ukryj Podobne zadania

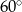W ostrosłupie prawidłowym trójkątnym krawędź podstawy ma długość 6. Oblicz objętość tego ostrosłupa jeżeli kąt nachylenia krawędzi bocznej do podstawy ma miarę 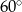60∘ .

W ostrosłupie prawidłowym trójkątnym 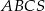ABCS o podstawie 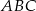ABC wysokość jest równa 3, a kąt między sąsiednimi ścianami bocznymi ostrosłupa ma miarę 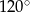12 0∘ . Oblicz objętość tego ostrosłupa.

Podstawą ostrosłupa 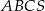ABCS jest trójkąt równoramienny 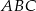ABC . Krawędź 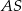jest wysokością ostrosłupa oraz 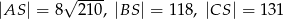√ ---- |AS | = 8 210, |BS | = 118 , |CS | = 131 . Oblicz objętość tego ostrosłupa.

Podstawą ostrosłupa prawidłowego jest kwadrat. Wysokość ściany bocznej tego ostrosłupa jest równa 22, a tangens kąta nachylenia ściany bocznej ostrosłupa do płaszczyzny jego podstawy jest równy 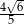√ - 4--6 5 . Oblicz objętość tego ostrosłupa.

Kapsuła lądownika ma kształt stożka zakończonego w podstawie półkulą o tym samym promieniu co promień podstawy stożka. Wysokość stożka jest o 1 m większa niż promień półkuli. Objętość stożka stanowi objętości całej kapsuły. Oblicz objętość kapsuły lądownika.

Narożnik między dwiema ścianami i suﬁtem prostopadłościennego pokoju należy zamaskować trójkątnym fragmentem płyty gipsowo-kartonowej (patrz rysunek). Wiedząc, że 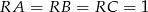RA = RB = RC = 1 m, oblicz objętość narożnika zamaskowanego tą płytą. Wynik zaokrąglij do 0,01 m 3 .

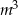W prostopadłościanie pola trzech ścian o wspólnym wierzchołku są równe 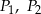P 1, P2 i 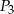. Oblicz objętość tego prostopadłościanu.

W ostrosłupie, którego podstawą jest trójkąt równoboczny o boku , jedna z krawędzi bocznych jest prostopadła do podstawy. Dwie pozostałe krawędzie tworzą z podstawą kąty o mierze . Znajdź pole największej ściany bocznej oraz tangens kąta nachylenia tej ściany do płaszczyzny podstawy.

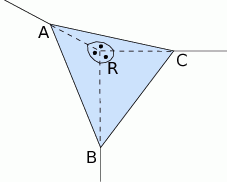
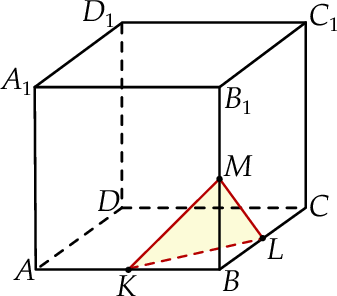
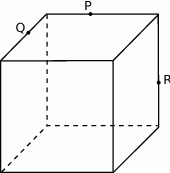
Przez środki trzech różnych krawędzi sześcianu 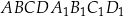ABCDA 1B1C 1D1 wychodzących z wierzchołka 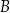poprowadzono płaszczyznę, która wyznaczyła przekrój bryły – trójkąt 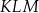KLM . Oblicz odległość wierzchołka 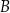od tego przekroju, jeżeli wiadomo, że długość krawędzi sześcianu wynosi 8.

ZINFO-FIGURE

Rozpatrujemy wszystkie stożki o tworzącej długości 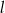. Oblicz wysokość i promień podstawy tego stożka, którego objętość jest największa. Oblicz tę największą objętość.

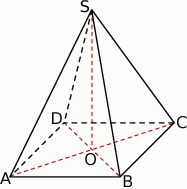
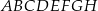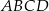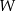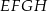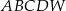Dany jest sześcian ABCDEF GH o krawędzi długości 9. Wierzchołki podstawy ABCD sześcianu połączono odcinkami z punktem , który jest punktem przecięcia przekątnych podstawy EF GH . Otrzymano w ten sposób ostrosłup prawidłowy czworokątny ABCDW .

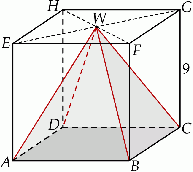
Oblicz cosinus kąta nachylenia krawędzi bocznej ostrosłupa do płaszczyzny podstawy.

Ukryj Podobne zadania

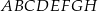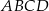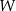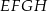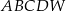Dany jest graniastosłup prawidłowy czworokątny ABCDEF GH o krawędzi podstawy równej 9 i wysokości równej 12. Wierzchołki podstawy ABCD graniastosłupa połączono odcinkami z punktem , który jest punktem przecięcia przekątnych podstawy EF GH . Otrzymano w ten sposób ostrosłup prawidłowy czworokątny ABCDW .

Oblicz cosinus kąta nachylenia krawędzi bocznej ostrosłupa do płaszczyzny podstawy.

Narysuj przekrój równoległościanu płaszczyzną 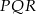PQR .

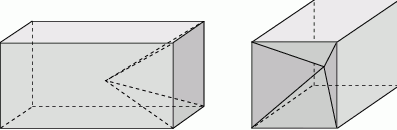
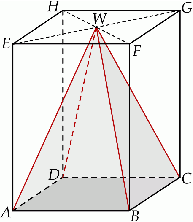
Z drewnianego prostopadłościanu o objętości 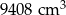3 940 8 cm i podstawie będącej kwadratem o boku 14 cm, wycięto ostrosłup prawidłowy czworokątny o wysokości równej połowie najdłuższej krawędzi prostopadłościanu. Otrzymano w ten sposób bryłę, której widok z dwóch stron przedstawiono na rysunku. Oblicz pole powierzchni całkowitej otrzymanej bryły.

Strona 18 z 28