Objętość ostrosłupa prawidłowego czworokątnego jest równa 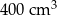 , a jego wysokość jest równa 12 cm. Oblicz pole powierzchni bocznej tego ostrosłupa. Zapisz obliczenia.
, a jego wysokość jest równa 12 cm. Oblicz pole powierzchni bocznej tego ostrosłupa. Zapisz obliczenia.
/Szkoła średnia/Geometria/Stereometria
W graniastosłupie prawidłowym czworokątnym o objętości równej 108 stosunek długości krawędzi podstawy do wysokości graniastosłupa jest równy  . Przekątna tego graniastosłupa jest nachylona do płaszczyzny jego podstawy pod kątem
. Przekątna tego graniastosłupa jest nachylona do płaszczyzny jego podstawy pod kątem  (zobacz rysunek).
(zobacz rysunek).
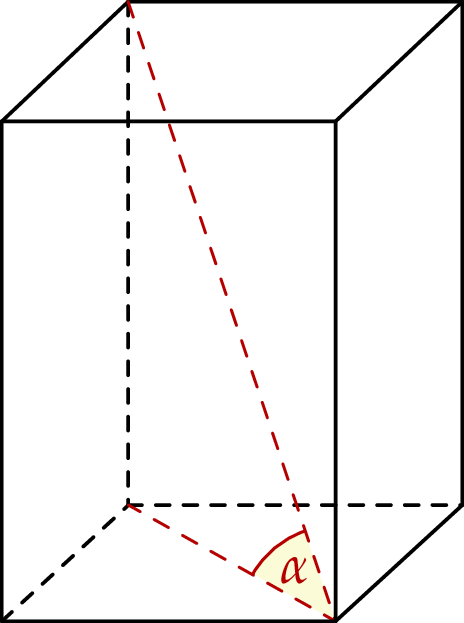
Oblicz cosinus kąta  oraz pole powierzchni całkowitej tego graniastosłupa.
oraz pole powierzchni całkowitej tego graniastosłupa.
Krawędź boczna ostrosłupa prawidłowego trójkątnego jest dwa razy dłuższa od krawędzi podstawy. Krawędź podstawy jest równa  . Oblicz pole powierzchni bocznej i sinus połowy kąta między ścianami bocznymi ostrosłupa.
. Oblicz pole powierzchni bocznej i sinus połowy kąta między ścianami bocznymi ostrosłupa.
Krawędź boczna ostrosłupa prawidłowego czworokątnego jest dwa razy dłuższa od krawędzi podstawy. Oblicz cosinus kąta między sąsiednimi ścianami bocznymi.
W ostrosłupie prawidłowym czworokątnym pole podstawy jest dwa razy większe od pola ściany bocznej. Oblicz cosinus kąta między sąsiednimi ścianami bocznymi tego ostrosłupa.
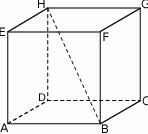
Podstawą graniastosłupa  jest prostokąt
jest prostokąt  (zobacz rysunek), którego krótszy bok ma długość 3. Przekątna prostokąta
(zobacz rysunek), którego krótszy bok ma długość 3. Przekątna prostokąta 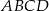 tworzy z jego dłuższym bokiem kąt
tworzy z jego dłuższym bokiem kąt 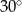 . Przekątna
. Przekątna 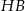 graniastosłupa tworzy z płaszczyzną jego podstawy kąt
graniastosłupa tworzy z płaszczyzną jego podstawy kąt 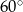 stopni. Oblicz objętość tego graniastosłupa.
stopni. Oblicz objętość tego graniastosłupa.
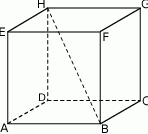
Podstawą graniastosłupa  jest prostokąt
jest prostokąt  (zobacz rysunek), którego dłuższy bok ma długość 6. Przekątna prostokąta
(zobacz rysunek), którego dłuższy bok ma długość 6. Przekątna prostokąta  tworzy z jego krótszym bokiem kąt
tworzy z jego krótszym bokiem kąt 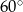 . Przekątna
. Przekątna 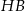 graniastosłupa tworzy z płaszczyzną jego podstawy kąt
graniastosłupa tworzy z płaszczyzną jego podstawy kąt 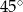 stopni. Oblicz objętość tego graniastosłupa.
stopni. Oblicz objętość tego graniastosłupa.
Dany jest ostrosłup prawidłowy czworokątny o objętości 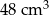 . Ściana boczna jest nachylona do podstawy pod takim kątem
. Ściana boczna jest nachylona do podstawy pod takim kątem  , że
, że 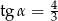 . Wyznacz pole powierzchni bocznej tego ostrosłupa.
. Wyznacz pole powierzchni bocznej tego ostrosłupa.
Krawędź boczna ostrosłupa prawidłowego czworokątnego wpisanego w kulę o promieniu 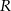 tworzy z płaszczyzną podstawy kąt
tworzy z płaszczyzną podstawy kąt  . Oblicz pole powierzchni całkowitej tego ostrosłupa.
. Oblicz pole powierzchni całkowitej tego ostrosłupa.
Na narysowanej poniżej siatce sześcianu zaznaczono trzy środki ścian sześcianu.
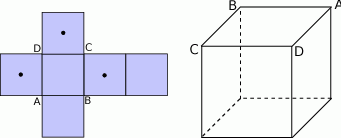
- Zaznacz na powierzchni sześcianu trzy punkty
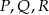 odpowiadające środkom ścian wskazanym na jego siatce.
odpowiadające środkom ścian wskazanym na jego siatce. - Wiedząc, że krawędź sześcianu ma długość 1, oblicz pole trójkąta
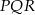 .
.
W graniastosłupie prawidłowym trójkątnym pole powierzchni bocznej równa się sumie pól obu podstaw. Oblicz tangens kąta nachylenia przekątnej ściany bocznej do sąsiedniej ściany bocznej.
Podstawą ostrosłupa 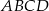 jest trójkąt równoboczny
jest trójkąt równoboczny 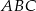 o boku długości
o boku długości 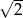 . Wszystkie ściany boczne są równoramiennymi trójkątami prostokątnymi. Punkt
. Wszystkie ściany boczne są równoramiennymi trójkątami prostokątnymi. Punkt 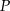 został wybrany wewnątrz ostrosłupa w ten sposób, że wysokości ostrosłupów
został wybrany wewnątrz ostrosłupa w ten sposób, że wysokości ostrosłupów 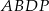 ,
, 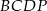 ,
, 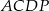 ,
, 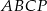 opuszczone z wierzchołka
opuszczone z wierzchołka 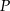 mają tę samą długość
mają tę samą długość 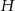 . Sporządź rysunek ostrosłupa i oblicz
. Sporządź rysunek ostrosłupa i oblicz 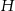 .
.
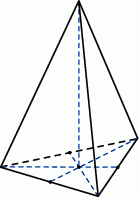
Dany jest ostrosłup prawidłowy trójkątny, w którym krawędź podstawy ma długość  i krawędź boczna jest od niej dwa razy dłuższa. Oblicz cosinus kąta między krawędzią boczną i krawędzią podstawy ostrosłupa. Narysuj przekrój ostrosłupa płaszczyzną przechodzącą przez krawędź podstawy i środek przeciwległej krawędzi bocznej i oblicz pole tego przekroju.
i krawędź boczna jest od niej dwa razy dłuższa. Oblicz cosinus kąta między krawędzią boczną i krawędzią podstawy ostrosłupa. Narysuj przekrój ostrosłupa płaszczyzną przechodzącą przez krawędź podstawy i środek przeciwległej krawędzi bocznej i oblicz pole tego przekroju.
Dany jest graniastosłup prawidłowy trójkątny 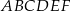 o podstawach
o podstawach 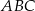 i
i 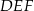 i krawędziach bocznych
i krawędziach bocznych 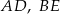 i
i 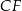 , które mają długość 13. Oblicz pole powierzchni całkowitej i objętość tego graniastosłupa jeżeli pole trójkąta
, które mają długość 13. Oblicz pole powierzchni całkowitej i objętość tego graniastosłupa jeżeli pole trójkąta 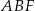 stanowi
stanowi 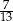 pola ściany bocznej
pola ściany bocznej 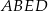 .
.
Podstawą ostrosłupa 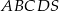 jest czworokąt
jest czworokąt 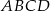 . Przekątna
. Przekątna 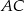 tego czworokąta ma długość
tego czworokąta ma długość 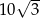 , a kąt
, a kąt 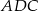 ma miarę
ma miarę 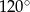 . Każda krawędź boczna tego ostrosłupa ma tę samą długość 26. Oblicz odległość środka wysokości tego ostrosłupa od krawędzi
. Każda krawędź boczna tego ostrosłupa ma tę samą długość 26. Oblicz odległość środka wysokości tego ostrosłupa od krawędzi 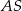 .
.
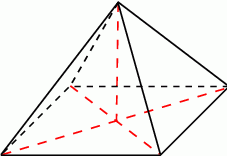
Podstawą ostrosłupa 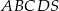 jest czworokąt
jest czworokąt 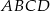 . Przekątna
. Przekątna 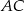 tego czworokąta ma długość
tego czworokąta ma długość 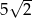 , a kąt
, a kąt 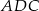 ma miarę
ma miarę 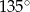 . Każda krawędź boczna tego ostrosłupa ma tę samą długość 13. Oblicz sumę odległości spodka wysokości ostrosłupa od krawędzi bocznych
. Każda krawędź boczna tego ostrosłupa ma tę samą długość 13. Oblicz sumę odległości spodka wysokości ostrosłupa od krawędzi bocznych 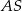 ,
,  ,
,  i
i  .
.
Dany jest ostrosłup prawidłowy czworokątny, w którym wszystkie krawędzie mają równą długość. Zaznacz na rysunku kąt utworzony przez dwie sąsiednie ściany boczne tego ostrosłupa i oblicz cosinus tego kąta.
Oblicz objętość kuli wiedząc że jej pole powierzchni jest równe 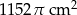 .
.
Oblicz objętość kuli wiedząc że jej pole powierzchni jest równe 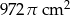 .
.
W stożek, którego wysokość ma długość 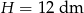 , a promień jego podstawy ma długość
, a promień jego podstawy ma długość 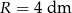 wpisano walec, o podstawach równoległych do podstawy stożka. Jakie powinny być wymiary walca, aby jego objętość była największa?
wpisano walec, o podstawach równoległych do podstawy stożka. Jakie powinny być wymiary walca, aby jego objętość była największa?
Objętość ostrosłupa prawidłowego trójkątnego 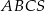 jest równa
jest równa 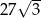 . Długość krawędzi
. Długość krawędzi 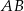 podstawy ostrosłupa jest równa 6 (zobacz rysunek). Oblicz pole powierzchni całkowitej tego ostrosłupa.
podstawy ostrosłupa jest równa 6 (zobacz rysunek). Oblicz pole powierzchni całkowitej tego ostrosłupa.
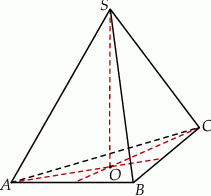
Objętość ostrosłupa prawidłowego trójkątnego 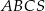 jest równa
jest równa 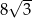 . Długość krawędzi
. Długość krawędzi 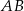 podstawy ostrosłupa jest równa 4 (zobacz rysunek). Oblicz pole powierzchni całkowitej tego ostrosłupa.
podstawy ostrosłupa jest równa 4 (zobacz rysunek). Oblicz pole powierzchni całkowitej tego ostrosłupa.
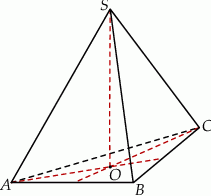
Płaszczyzna 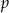 jest styczna do kuli wpisanej w sześcian
jest styczna do kuli wpisanej w sześcian 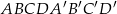 o krawędzi długości
o krawędzi długości 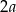 oraz przecina krawędzie
oraz przecina krawędzie 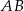 ,
, 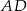 i
i 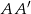 w takich punktach
w takich punktach 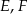 i
i 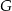 odpowiednio, że
odpowiednio, że 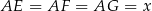 . Wykonaj odpowiedni rysunek i wyznacz
. Wykonaj odpowiedni rysunek i wyznacz  .
.
Podstawą ostrosłupa jest trójkąt równoramienny o ramieniu długości 10 i podstawie długości 12. Wszystkie krawędzie boczne ostrosłupa mają długość 7. Oblicz objętość i pole powierzchni bocznej tego ostrosłupa.
Podstawą ostrosłupa o objętości 30 jest trójkąt równoramienny o ramieniu długości 5 i podstawie długości 6. Oblicz pole powierzchni bocznej ostrosłupa wiedząc, że wszystkie krawędzie boczne mają jednakową długość.
Suma długości trzech krawędzi prostopadłościanu wychodzących z jednego wierzchołka jest równa 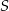 . Długość jednej z tych krawędzi jest dwa razy większa od drugiej. Oblicz promień sfery opisanej na tym z rozważanych prostopadłościanów, którego objętość jest największa.
. Długość jednej z tych krawędzi jest dwa razy większa od drugiej. Oblicz promień sfery opisanej na tym z rozważanych prostopadłościanów, którego objętość jest największa.

