Stereometria/Geometria/Szkoła średnia - zadania z matematyki

/Szkoła średnia/Geometria/Stereometria

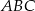Trójkąt ABC jest podstawą prawidłowego ostrosłupa 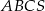ABCS , którego krawędź boczna ma długość 10. Punkt 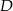jest środkiem wysokości 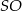ostrosłupa oraz 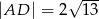√ --- |AD | = 2 13 . Oblicz objętość tego ostrosłupa.

Dany jest graniastosłup prawidłowy sześciokątny o podstawie 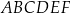ABCDEF i polu powierzchni bocznej równym . Kąt między przekątnymi ścian bocznych wychodzącymi z wierzchołka ma miarę 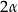. Objętość tego graniastosłupa jest równa

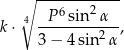
------------ ∘ 6 2 k ⋅ 4 -P--sin--α--, 3− 4sin2α

gdzie 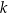jest stałym współczynnikiem liczbowym. Oblicz współczynnik .

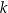Oblicz cosinus kąta między ścianą boczną i płaszczyzną podstawy ostrosłupa prawidłowego trójkątnego, jeżeli wiadomo, że promień okręgu opisanego na podstawie, wysokość ostrosłupa i krawędź boczna tworzą trójkąt równoramienny.

Ukryj Podobne zadania

Oblicz cosinus kąta między krawędzią boczną i krawędzią podstawy ostrosłupa prawidłowego trójkątnego, jeżeli wiadomo, że promień okręgu opisanego na podstawie, wysokość ostrosłupa i krawędź boczna tworzą trójkąt równoramienny.

Oblicz odległość środka ściany sześcianu o krawędzi długości od przekątnej tego sześcianu.

Ukryj Podobne zadania

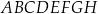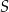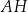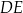Dany jest sześcian ABCDEF GH o krawędzi długości 6. Punkt jest punktem przecięcia przekątnych i ściany bocznej 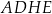ADHE (zobacz rysunek).

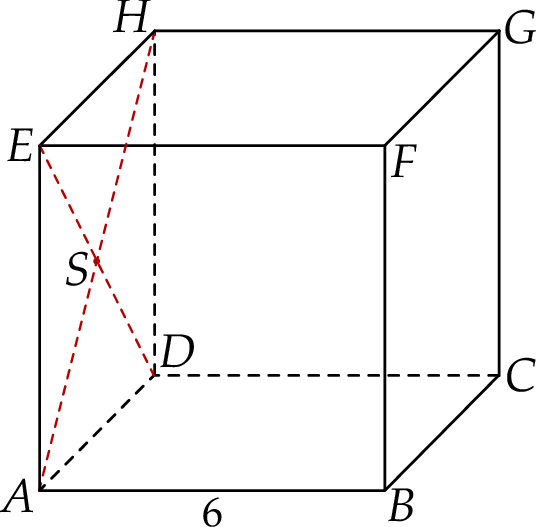
ZINFO-FIGURE

Oblicz wysokość trójkąta 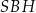SBH poprowadzoną z punktu 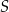na bok 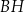tego trójkąta.

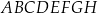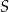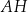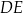Dany jest sześcian ABCDEF GH o krawędzi długości 3. Punkt jest punktem przecięcia przekątnych i ściany bocznej 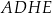ADHE (zobacz rysunek).

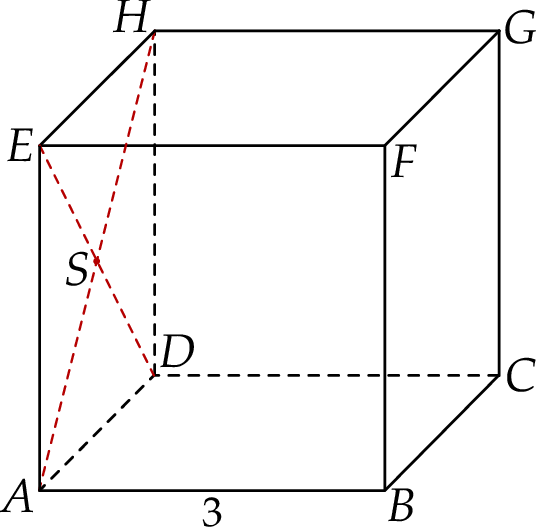
ZINFO-FIGURE

Oblicz wysokość trójkąta 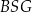BSG poprowadzoną z punktu 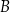na bok 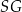tego trójkąta.

Na półkuli o promieniu 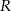opisano stożek w ten sposób, że środek podstawy stożka pokrywa się ze środkiem kuli. Jaka jest najmniejsza możliwa objętość tego stożka?

Podstawą prostopadłościanu jest kwadrat o boku długości 4, a wysokość prostopadłościanu jest równa 8. Połączono odcinkami środki trzech krawędzi prostopadłościanu, które mają wspólny wierzchołek i otrzymano trójkąt 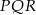P QR

Oblicz długości boków trójkąta .
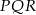Wyznacz sinusy kątów trójkąta .

Krawędź podstawy graniastosłupa prawidłowego sześciokątnego ma długość . Przekątne sąsiednich ścian bocznych poprowadzone z tego samego wierzchołka są prostopadłe. Oblicz objętość tego graniastosłupa.

W ostrosłupie prawidłowym trójkątnym krawędź boczna ma długość 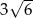√ -- 3 6 , a krawędź podstawy ma długość 12. Oblicz miarę kąta utworzonego przez dwie sąsiednie ściany boczne.

Wysokość czworościanu foremnego ma długość 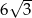√ -- 6 3 . Oblicz jego objętość i pole powierzchni całkowitej.

Podstawą ostrosłupa 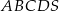ABCDS jest równoległobok 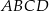ABCD o przekątnej długości 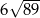√ --- 6 89 i bokach długości 32 i 34. Pole powierzchni bocznej jednej ze ścian bocznych ostrosłupa jest mniejsze od pola powierzchni sąsiedniej ściany bocznej i jest równe 1808. Spodek wysokości ostrosłupa pokrywa się z punktem przecięcia przekątnych równoległoboku 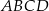ABCD , a jego ściany boczne są trójkątami ostrokątnymi. 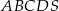Oblicz długość krótszej z krawędzi bocznych ostrosłupa ABCDS .

Spodek wysokości ostrosłupa 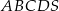ABCDS pokrywa się ze środkiem rombu 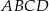ABCD w jego podstawie oraz 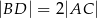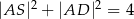|BD | = 2|AC | , |AS |2 + |AD |2 = 4 . Oblicz objętość ostrosłupa 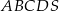ABCDS jeżeli wiadomo, że pole trójkąta 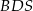BDS jest największe możliwe.

Tekturowy karton ma mieć kształt prostopadłościanu, którego podstawa jest prostokątem o jednym z boków dłuższym od drugiego o 24 cm. Suma wszystkich krawędzi tego prostopadłościanu ma być równa 480 cm.

Napisz wzór funkcji 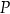wyrażającej całkowite pole zewnętrznej powierzchni kartonu, w zależności od długości krótszej krawędzi jego podstawy. Podaj dziedzinę funkcji .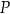
Oblicz jakie powinny być wymiary tego kartonu tak, aby łączne pole powierzchni jego ścian było największe możliwe.

Przekątna graniastosłupa prawidłowego czworokątnego o długości 10 cm jest nachylona do płaszczyzny podstawy pod kątem 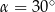α = 30∘ . Oblicz objętość tego graniastosłupa.

Ukryj Podobne zadania

Przekątna graniastosłupa prawidłowego czworokątnego o długości 8 cm jest nachylona do płaszczyzny podstawy pod kątem 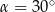α = 30∘ . Oblicz objętość tego graniastosłupa.

Podstawa ostrosłupa prawidłowego czworokątnego ma pole 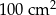2 100 cm , a jego pole powierzchni bocznej jest równe 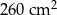260 cm 2 . Oblicz objętość tego ostrosłupa.

Suma długości wysokości i długości jednej krawędzi podstawy graniastosłupa prawidłowego czworokątnego jest równa 2. Jaką najmniejszą długość może mieć przekątna takiego graniastosłupa.

Wysokość ostrosłupa prawidłowego czworokątnego tworzy ze ścianą boczną kąt o mierze 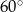60 ∘ . Pole powierzchni bocznej ostrosłupa jest równe 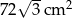√ -- 72 3 cm 2 . Oblicz objętość ostrosłupa.

Kąt rozwarcia stożka jest równy 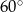∘ 60 . Promień podstawy stożka ma długość 4. Oblicz pole powierzchni bocznej stożka.

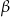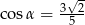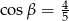Przekątna prostopadłościanu ma długość 5 i tworzy z dwoma ścianami prostopadłościanu kąty i takie, że √- co sα = 3-2- 5 i co sβ = 4 5 . Oblicz objętość tego prostopadłościanu.

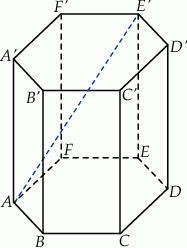
Przekątna 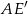′ AE graniastosłupa prawidłowego sześciokątnego ma długość 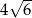√ -- 4 6 i jest nachylona do płaszczyzny podstawy pod kątem 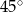45∘ . Oblicz objętość tego graniastosłupa.

Dany jest ostrosłup, którego podstawą jest trójkąt równoboczny o boku 6. Jedna z krawędzi bocznych tego ostrosłupa ma długość 8 i jest prostopadła do płaszczyzny podstawy. Oblicz objętość tego ostrosłupa.

Strona 20 z 28