Stosunek pola powierzchni bocznej stożka do pola jego powierzchni całkowitej jest równy  . Wyznacz miarę kąta nachylenia tworzącej stożka do płaszczyzny podstawy.
. Wyznacz miarę kąta nachylenia tworzącej stożka do płaszczyzny podstawy.
/Szkoła średnia/Geometria/Stereometria
Podstawą graniastosłupa prostego jest romb, którego krótsza przekątna ma długość  , a kąt ostry miarę
, a kąt ostry miarę 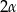 . Pole przekroju wyznaczonego przez krawędź boczną graniastosłupa i dłuższą przekątną podstawy wynosi
. Pole przekroju wyznaczonego przez krawędź boczną graniastosłupa i dłuższą przekątną podstawy wynosi 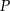 . Oblicz długość dłuższej przekątnej graniastosłupa, wykonaj rysunek bryły i zaznacz w nim właściwy przekrój.
. Oblicz długość dłuższej przekątnej graniastosłupa, wykonaj rysunek bryły i zaznacz w nim właściwy przekrój.
Podstawą ostrosłupa prawidłowego 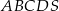 jest kwadrat
jest kwadrat 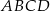 . Punkt
. Punkt 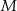 jest środkiem odcinka
jest środkiem odcinka 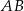 , a punkt
, a punkt 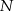 jest środkiem odcinka
jest środkiem odcinka 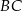 . Trójkąt
. Trójkąt 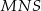 jest równoboczny i jego bok ma długość
jest równoboczny i jego bok ma długość 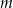 . Oblicz objętość ostrosłupa
. Oblicz objętość ostrosłupa 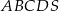 i kąt nachylenia ściany bocznej do płaszczyzny podstawy tego ostrosłupa.
i kąt nachylenia ściany bocznej do płaszczyzny podstawy tego ostrosłupa.
Wykaż, że objętość sześcianu jest sześć razy większa od objętości ośmiościanu foremnego, wyznaczonego przez środki ścian tego sześcianu.
Trójkąt o bokach długości 5, 8 i 9 obraca się dookoła najdłuższego boku. Oblicz objętość powstałej bryły.
Trójkąt o bokach długości 17, 28 i 33 obraca się dookoła najdłuższego boku. Oblicz objętość powstałej bryły.
Trójkąt o bokach długości 3, 5 i 7 obraca się dookoła najdłuższego boku. Oblicz objętość powstałej bryły.
Trapez prostokątny obraca się wokół boku tworzącego z podstawami kąty proste. Podstawy trapezu mają długość odpowiednio 10 cm i 7 cm. Pole trapezu wynosi 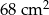 . Oblicz objętość otrzymanej bryły.
. Oblicz objętość otrzymanej bryły.
Sześcian 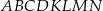 przecięto płaszczyzną przechodzącą przez przekątną
przecięto płaszczyzną przechodzącą przez przekątną 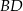 podstawy, która jest nachylona do płaszczyzny podstawy pod kątem
podstawy, która jest nachylona do płaszczyzny podstawy pod kątem  takim, że
takim, że 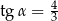 (zobacz rysunek).
(zobacz rysunek).
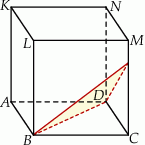
Odległość wierzchołka 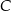 od płaszczyzny tego przekroju jest równa 6. Oblicz objętość sześcianu
od płaszczyzny tego przekroju jest równa 6. Oblicz objętość sześcianu 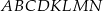 .
.
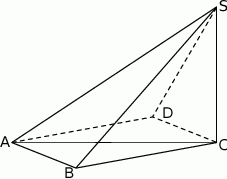
Podstawą ostrosłupa 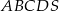 jest romb
jest romb 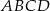 . Krawędź
. Krawędź 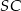 jest prostopadła do płaszczyzny podstawy, krawędź
jest prostopadła do płaszczyzny podstawy, krawędź 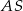 ma długość 4 i jest nachylona do płaszczyzny podstawy pod kątem
ma długość 4 i jest nachylona do płaszczyzny podstawy pod kątem 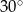 . Krawędź
. Krawędź 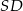 ma długość
ma długość 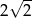 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Wysokość prawidłowego ostrosłupa sześciokątnego ma długość 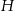 , a krawędź podstawy ma długość
, a krawędź podstawy ma długość  . Wyznacz pole przekroju wyznaczonego przez krótszą przekątną podstawy i wierzchołek ostrosłupa.
. Wyznacz pole przekroju wyznaczonego przez krótszą przekątną podstawy i wierzchołek ostrosłupa.
Oblicz długość odcinka łączącego środki przeciwległych krawędzi czworościanu foremnego o krawędzi długości  .
.
Pole powierzchni całkowitej prostopadłościanu jest równe 198. Stosunki długości krawędzi prostopadłościanu wychodzących z tego samego wierzchołka prostopadłościanu to 1 : 2 : 3. Oblicz długość przekątnej tego prostopadłościanu.
Oblicz wysokość i objętość ostrosłupa prawidłowego sześciokątnego o krawędzi podstawy 4 cm i krawędzi bocznej 10 cm.
Podstawą ostrosłupa jest prostokąt o polu 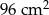 kwadratowych. Stosunek długości boków tego prostokąta wynosi 2:3. Krawędzie boczne ostrosłupa są nachylone do płaszczyzny podstawy pod kątem
kwadratowych. Stosunek długości boków tego prostokąta wynosi 2:3. Krawędzie boczne ostrosłupa są nachylone do płaszczyzny podstawy pod kątem 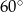 . Oblicz pole powierzchni całkowitej tej bryły.
. Oblicz pole powierzchni całkowitej tej bryły.
Dany jest graniastosłup prawidłowy trójkątny (zobacz rysunek). Pole powierzchni całkowitej tego graniastosłupa jest równe 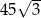 . Pole podstawy graniastosłupa jest równe polu jednej ściany bocznej. Oblicz objętość tego graniastosłupa.
. Pole podstawy graniastosłupa jest równe polu jednej ściany bocznej. Oblicz objętość tego graniastosłupa.
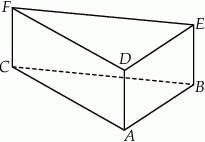
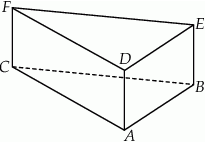
Dany jest graniastosłup prawidłowy trójkątny (zobacz rysunek). Objętość tego graniastosłupa jest równa 324. Pole podstawy graniastosłupa jest równe polu jednej ściany bocznej. Oblicz pole powierzchni całkowitej tego graniastosłupa.
W ostrosłup prawidłowy czworokątny wpisano sześcian tak, że jego cztery wierzchołki należą do krawędzi bocznych ostrosłupa, a pozostałe do płaszczyzny podstawy. Oblicz długość krawędzi sześcianu, jeżeli wysokość ostrosłupa jest równa 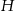 , a długość jego krawędzi podstawy jest równa
, a długość jego krawędzi podstawy jest równa  .
.
W graniastosłupie prawidłowym trójkątnym przekątna ściany bocznej tworzy z płaszczyzną podstawy kąt o mierze równej 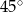 . Oblicz pole powierzchni bocznej tego graniastosłupa, wiedząc, że jego objętość jest równa
. Oblicz pole powierzchni bocznej tego graniastosłupa, wiedząc, że jego objętość jest równa 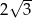 .
.
W graniastosłupie prawidłowym trójkątnym przekątna ściany bocznej tworzy z płaszczyzną podstawy kąt o mierze równej 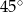 . Oblicz pole powierzchni bocznej tego graniastosłupa, wiedząc, że jego objętość jest równa
. Oblicz pole powierzchni bocznej tego graniastosłupa, wiedząc, że jego objętość jest równa 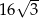 .
.
Rozpatrujemy wszystkie możliwe drewniane szkielety o kształcie przedstawionym na rysunku, wykonane z listewek. Każda z tych listewek ma kształt prostopadłościanu o podstawie kwadratu o boku długości  . Wymiary szkieletu zaznaczono na rysunku.
. Wymiary szkieletu zaznaczono na rysunku.
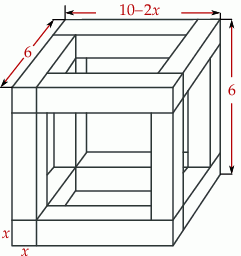
- Wyznacz objętość
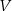 drewna potrzebnego do budowy szkieletu jako funkcję zmiennej
drewna potrzebnego do budowy szkieletu jako funkcję zmiennej  .
. - Wyznacz dziedzinę funkcji
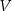 .
. - Oblicz tę wartość
 , dla której zbudowany szkielet jest możliwie najcięższy, czyli kiedy funkcja
, dla której zbudowany szkielet jest możliwie najcięższy, czyli kiedy funkcja 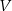 osiąga wartość największą. Oblicz tę największą objętość.
osiąga wartość największą. Oblicz tę największą objętość.
Rozpatrujemy wszystkie możliwe drewniane szkielety o kształcie przedstawionym na rysunku, wykonane z listewek. Każda z tych listewek ma kształt prostopadłościanu o podstawie kwadratu o boku długości  . Wymiary szkieletu zaznaczono na rysunku.
. Wymiary szkieletu zaznaczono na rysunku.
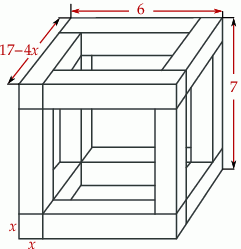
- Wyznacz objętość
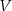 drewna potrzebnego do budowy szkieletu jako funkcję zmiennej
drewna potrzebnego do budowy szkieletu jako funkcję zmiennej  .
. - Wyznacz dziedzinę funkcji
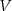 .
. - Oblicz tę wartość
 , dla której zbudowany szkielet jest możliwie najcięższy, czyli kiedy funkcja
, dla której zbudowany szkielet jest możliwie najcięższy, czyli kiedy funkcja 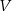 osiąga wartość największą. Oblicz tę największą objętość.
osiąga wartość największą. Oblicz tę największą objętość.
Podstawa stożka o kącie rozwarcia 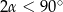 jest kołem wielkim kuli. Oblicz objętość tego stożka jeżeli jego powierzchnia boczna wycina z powierzchni kuli okrąg o promieniu
jest kołem wielkim kuli. Oblicz objętość tego stożka jeżeli jego powierzchnia boczna wycina z powierzchni kuli okrąg o promieniu  .
.
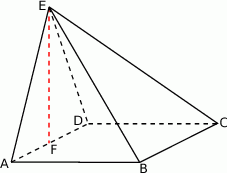
Podstawą ostrosłupa 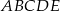 jest kwadrat
jest kwadrat 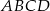 . Punkt
. Punkt 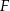 jest środkiem krawędzi
jest środkiem krawędzi 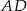 , odcinek
, odcinek 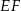 jest wysokością ostrosłupa. Oblicz objętość ostrosłupa, jeśli wiadomo, że
jest wysokością ostrosłupa. Oblicz objętość ostrosłupa, jeśli wiadomo, że 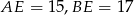 .
.
W ostrosłup prawidłowy czworokątny o wysokości 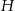 wpisano sześcian tak, że cztery jego wierzchołki należą do krawędzi bocznych ostrosłupa, a cztery pozostałe należą do płaszczyzny jego podstawy. Oblicz dla jakiej długości krawędzi podstawy ostrosłupa stosunek objętości ostrosłupa do objętości sześcianu jest najmniejszy możliwy.
wpisano sześcian tak, że cztery jego wierzchołki należą do krawędzi bocznych ostrosłupa, a cztery pozostałe należą do płaszczyzny jego podstawy. Oblicz dla jakiej długości krawędzi podstawy ostrosłupa stosunek objętości ostrosłupa do objętości sześcianu jest najmniejszy możliwy.

