Proste o równaniach: 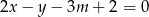 i
i 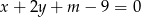 przecinają się w punkcie
przecinają się w punkcie 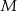 . Dla jakich wartości
. Dla jakich wartości 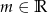 punkt
punkt 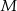 należy do prostej o równaniu
należy do prostej o równaniu 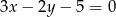 .
.
/Szkoła średnia/Geometria/Geometria analityczna/Równanie prostej/Z parametrem
Prosta 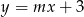 tworzy z dodatnimi półosiami układu współrzędnych trójkąt o polu 7. Wyznacz
tworzy z dodatnimi półosiami układu współrzędnych trójkąt o polu 7. Wyznacz 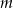 .
.
Prosta 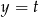 przecina proste
przecina proste 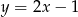 i
i 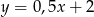 odpowiednio w punktach
odpowiednio w punktach 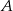 i
i 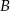 .
.
- Wyraź długość odcinka
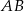 jako funkcję zmiennej
jako funkcję zmiennej 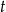 .
. - Wyznacz takie punkty
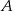 i
i 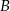 , aby długość odcinka
, aby długość odcinka 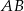 była równa 3.
była równa 3.
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 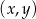 , dane są proste
, dane są proste 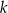 oraz
oraz 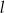 o równaniach
o równaniach
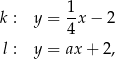
gdzie  jest pewną liczbą rzeczywistą. Proste
jest pewną liczbą rzeczywistą. Proste 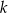 i
i 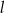 są prostopadłe. Wyznacz ich punkt przecięcia.
są prostopadłe. Wyznacz ich punkt przecięcia.
Wyznacz te wartości parametru 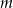 , dla których punkt przecięcia się prostych o równaniach
, dla których punkt przecięcia się prostych o równaniach 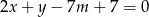 i
i 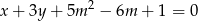 należy do 3 ćwiartki układu współrzędnych.
należy do 3 ćwiartki układu współrzędnych.
Dla jakich wartości parametru 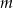 punkt przecięcia się prostych
punkt przecięcia się prostych 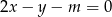 i
i 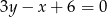 należy do prostej
należy do prostej 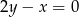 . Podaj współrzędne tego punktu i oblicz jego odległość od prostej
. Podaj współrzędne tego punktu i oblicz jego odległość od prostej 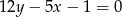 .
.
Zbadaj dla jakich wartości parametru 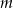 punkt przecięcia się prostych
punkt przecięcia się prostych 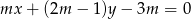 i
i 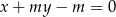 należy do prostokąta o wierzchołkach
należy do prostokąta o wierzchołkach 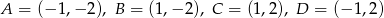 ?
?
Dla jakich wartości parametru 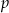 proste
proste 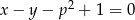 i
i 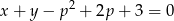 przecinają się w punkcie należącym do wnętrza prostokąta o wierzchołkach
przecinają się w punkcie należącym do wnętrza prostokąta o wierzchołkach 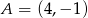 ,
, 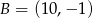 ,
, 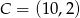 ,
, 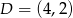 ?
?

