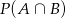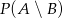W urnie znajdują się 52 kule, które mogą się różnić wyłącznie kolorem. Wśród nich jest 26 kul białych, 6 kul czarnych, 12 niebieskich i 8 zielonych. Z tej urny losujemy czterokrotnie jedną kulę bez zwracania. Oblicz prawdopodobieństwo wylosowania czterech kul, wśród których są 2 białe i 2 niebieskie. Wynik podaj w postaci ułamka nieskracalnego.
/Szkoła średnia/Prawdopodobieństwo
Z sześciu odcinków długości 1,3,5,6,7,9 wybieramy losowo trzy. Oblicz prawdopodobieństwo że można z nich zbudować trójkąt.
O zdarzeniach losowych 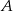 i
i 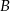 wiemy, że:
wiemy, że: 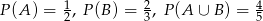 . Oblicz:
. Oblicz:
W wazonie stoi 12 czerwonych i 8 żółtych róż. Pani Krystyna wyjęła losowo dwie róże z wazonu. Oblicz prawdopodobieństwo, że wśród wybranych kwiatów jest przynajmniej jedna róża żółta.
Co jest bardziej prawdopodobne: wyrzucić dwa orły w trzech rzutach monetą, czy trzy orły w czterech rzutach?
Rzucamy cztery razy symetryczną monetą. Co jest bardziej prawdopodobne: wyrzucenie dokładnie jednej reszki czy wyrzucenie orła dwa razy z rzędu?
W garderobie pani Joanny wiszą 3 żakiety: biały, zielony i granatowy oraz 4 spódnice: czarna, biała, granatowa i szara. Oblicz prawdopodobieństwo zdarzenia, że wybierając losowo jeden żakiet i jedną spódnicę, pani Joanna skompletuje strój w jednym kolorze.
Dane są dwa podzbiory zbioru liczb całkowitych:
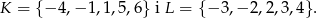
Z każdego z nich losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczb, których iloczyn jest dodatni.
Ze zbioru pięciu liczb 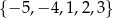 losujemy kolejno ze zwracaniem dwa razy po jednej liczbie. Zdarzenie
losujemy kolejno ze zwracaniem dwa razy po jednej liczbie. Zdarzenie 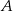 polega na wylosowaniu dwóch liczb, których iloczyn jest ujemny. Oblicz prawdopodobieństwo zdarzenia
polega na wylosowaniu dwóch liczb, których iloczyn jest ujemny. Oblicz prawdopodobieństwo zdarzenia 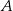 .
.
Dane są dwa podzbiory zbioru liczb całkowitych:
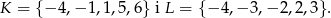
Z każdego z nich losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczb, których iloczyn jest dodatni.
Dane są dwa podzbiory zbioru liczb całkowitych:
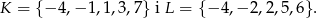
Z każdego z nich losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczb, których iloczyn jest ujemny.
Do windy na parterze budynku wsiadło 8 osób, po czym każda z nich w sposób losowy wysiadła na jednym z pięciu pięter budynku. Jakie jest prawdopodobieństwo, że na jednym z pięter wysiadło co najmniej 6 osób?
Do windy na parterze budynku wsiadło 8 osób, po czym każda z nich w sposób losowy wysiadła na jednym z pięciu pięter budynku. Jakie jest prawdopodobieństwo, że na dwóch różnych piętrach wysiadły po trzy osoby?
Liczby ze zbioru 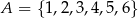 ustawiamy w losowy sposób w sześcioelementowy ciąg, przy czym każda liczba ze zbioru
ustawiamy w losowy sposób w sześcioelementowy ciąg, przy czym każda liczba ze zbioru 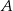 jest dokładnie jednym wyrazem tego ciągu. Oblicz prawdopodobieństwo tego, że iloczyn każdych dwóch sąsiednich wyrazów tego ciągu jest liczbą parzystą jeżeli wiadomo, że pierwszy wyraz tego ciągu jest liczbą nieparzystą.
jest dokładnie jednym wyrazem tego ciągu. Oblicz prawdopodobieństwo tego, że iloczyn każdych dwóch sąsiednich wyrazów tego ciągu jest liczbą parzystą jeżeli wiadomo, że pierwszy wyraz tego ciągu jest liczbą nieparzystą.
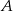 i
i 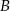 są takimi zdarzeniami losowymi zawartymi w
są takimi zdarzeniami losowymi zawartymi w 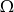 , że
, że 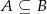 oraz
oraz 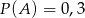 i
i 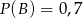 . Oblicz prawdopodobieństwo różnicy
. Oblicz prawdopodobieństwo różnicy 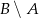 .
.
Doświadczenie losowe polega na tym, że losujemy jednocześnie trzy liczby ze zbioru
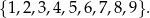
Oblicz prawdopodobieństwo warunkowe, że wśród wylosowanych liczb będzie liczba 3, pod warunkiem, że suma wylosowanych liczb będzie nieparzysta. Wynik przedstaw w postaci ułamka nieskracalnego.
Z liczb ośmioelementowego zbioru 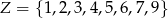 tworzymy ośmiowyrazowy ciąg, którego wyrazy się nie powtarzają. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że żadne dwie liczby parzyste nie są sąsiednimi wyrazami utworzonego ciągu. Wynik przedstaw w postaci ułamka zwykłego nieskracalnego.
tworzymy ośmiowyrazowy ciąg, którego wyrazy się nie powtarzają. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że żadne dwie liczby parzyste nie są sąsiednimi wyrazami utworzonego ciągu. Wynik przedstaw w postaci ułamka zwykłego nieskracalnego.
Ze zbioru 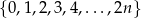 gdzie
gdzie 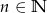 wylosowano jednocześnie 3 liczby. Prawdopodobieństwo, że suma wylosowanych liczb jest nieparzysta wynosi
wylosowano jednocześnie 3 liczby. Prawdopodobieństwo, że suma wylosowanych liczb jest nieparzysta wynosi 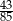 . Wyznacz ile liczb było w zbiorze.
. Wyznacz ile liczb było w zbiorze.
W urnie znajduje się 16 kul, które mogą się różnić wyłącznie kolorem. Wśród nich jest 10 kul białych i 6 kul czarnych. Z tej urny losujemy dwukrotnie jedną kulę bez zwracania. Oblicz prawdopodobieństwo wylosowania dwóch kul białych.
W urnie znajduje się 18 kul, które mogą się różnić wyłącznie kolorem. Wśród nich jest 6 kul białych i 12 kul czarnych. Z tej urny losujemy dwukrotnie jedną kulę bez zwracania. Oblicz prawdopodobieństwo wylosowania dwóch kul czarnych.
Rzucamy trzy razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo otrzymania iloczynu oczek równego 12.
Ze zbioru 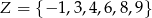 losujemy bez zwracania liczby
losujemy bez zwracania liczby  i
i 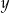 . Oblicz prawdopodobieństwa zdarzeń:
. Oblicz prawdopodobieństwa zdarzeń: 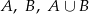 jeśli:
jeśli:
A – suma wylosowanych liczb jest nieparzysta;
B – wylosowane liczby spełniają warunek: 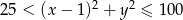 .
.
W urnie znajduje się dwa razy więcej kul białych niż czarnych. Losujemy z urny jednocześnie dwie kule. Prawdopodobieństwo wylosowania obu kul białych jest równe 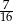 . Oblicz prawdopodobieństwo wylosowania kul różnych kolorów.
. Oblicz prawdopodobieństwo wylosowania kul różnych kolorów.
Łukasz w sposób losowy ustawia na jednej półce regału pewną liczbę książek. Wśród tych książek są trzy książki w języku angielskim, a wszystkie pozostałe są w języku polskim. Prawdopodobieństwo zdarzenia polegającego na tym, że trzy książki w języku angielskim znajdą się obok siebie jest równe 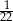 . Oblicz, ile książek w języku polskim zostało ustawionych na tej półce.
. Oblicz, ile książek w języku polskim zostało ustawionych na tej półce.
W pudełku znajdują się klocki o różnych kształtach i kolorach. Wiadomo, że prawdopodobieństwo wylosowania klocka, który ma kształt walca lub ma kolor czerwony jest równe 0,6. Prawdopodobieństwo, że losowo wybrany klocek czerwony jest walcem jest równe 0,25. Wiadomo też, że klocki czerwone stanowią 40% wszystkich klocków. Jakie jest prawdopodobieństwo, że losowo wybrany klocek w kształcie walca jest czerwony?
Ze zbioru wszystkich liczb naturalnych czterocyfrowych, których cyfra tysięcy i cyfra setek należą do zbioru 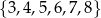 , a cyfra dziesiątek i cyfra jedności należą do zbioru
, a cyfra dziesiątek i cyfra jedności należą do zbioru 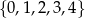 , losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy liczbę czterocyfrową, która jest podzielna przez 4.
, losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy liczbę czterocyfrową, która jest podzielna przez 4.