Jedenastu panów, wśród których są 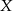 ,
, 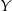 i
i 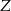 , ustawiamy losowo w szeregu. Oblicz prawdopodobieństwo, że pan
, ustawiamy losowo w szeregu. Oblicz prawdopodobieństwo, że pan 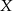 będzie stał obok pana
będzie stał obok pana 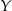 i pan
i pan 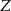 nie będzie stał obok pana
nie będzie stał obok pana 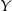 .
.
/Szkoła średnia/Prawdopodobieństwo
Rzucono kostką do gry trzy razy. Za pierwszym razem nie wyrzucono 4 oczek. Oblicz prawdopodobieństwo, że suma oczek w trzech rzutach jest równa 15.
Ze zbioru liczb dwucyfrowych losujemy jedną liczbę. Jakie jest prawdopodobieństwo, że iloczyn cyfr wylosowanej liczby jest dodatnią liczbą złożoną?
Na stole leżało 14 banknotów: 2 banknoty o nominale 100 zł, 2 banknoty o nominale 50 zł i 10 banknotów o nominale 20 zł. Wiatr zdmuchnął na podłogę 5 banknotów. Oblicz prawdopodobieństwo tego, że na podłodze leży dokładnie 130 zł. Odpowiedź podaj w postaci ułamka nieskracalnego.
Ze zbioru liczb 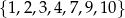 losujemy dwie liczby (mogą się powtarzać). Oblicz prawdopodobieństwo, że suma wylosowanych liczb jest parzysta.
losujemy dwie liczby (mogą się powtarzać). Oblicz prawdopodobieństwo, że suma wylosowanych liczb jest parzysta.
Dany jest pięcioelementowy zbiór 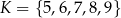 . Wylosowanie każdej liczby z tego zbioru jest jednakowo prawdopodobne. Ze zbioru
. Wylosowanie każdej liczby z tego zbioru jest jednakowo prawdopodobne. Ze zbioru 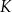 losujemy ze zwracaniem kolejno dwa razy po jednej liczbie i zapisujemy je w kolejności losowania. Oblicz prawdopodobieństwo zdarzenia
losujemy ze zwracaniem kolejno dwa razy po jednej liczbie i zapisujemy je w kolejności losowania. Oblicz prawdopodobieństwo zdarzenia 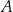 polegającego na tym, że suma wylosowanych liczb jest liczbą parzystą.
polegającego na tym, że suma wylosowanych liczb jest liczbą parzystą.
Na loterii jest  losów, w tym 4 wygrywające. Kupujemy 2 losy. Dla jakiej liczby
losów, w tym 4 wygrywające. Kupujemy 2 losy. Dla jakiej liczby  prawdopodobieństwo otrzymania co najmniej jednego losu wygrywającego jest równe
prawdopodobieństwo otrzymania co najmniej jednego losu wygrywającego jest równe 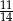 ?
?
Prawdopodobieństwa zdarzeń 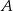 i
i 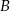 oraz zdarzeń do nich przeciwnych spełniają warunki:
oraz zdarzeń do nich przeciwnych spełniają warunki: 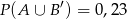 i
i 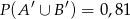 .
.
- Oblicz
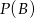 .
. - Wykaż, że jeżeli
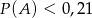 to
to 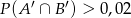 .
.
Pewna choroba dotyka 0,2% całej populacji i w początkowym stadium nie daje widocznych objawów chorobowych. W ramach profilaktyki stosuje się pewien test przesiewowy, który daje wynik pozytywny lub negatywny. Prawdopodobieństwo tego, że test wykonany na osobie chorej da wynik pozytywny (oznaczający chorobę), jest równe 0,99. Ponadto wiadomo, że prawdopodobieństwo tego, że test wykonany na osobie zdrowej da wynik negatywny, jest równe 0,98. Pan  poddał się testowi, który dał wynik pozytywny. Pozytywny wynik oznacza podejrzenie choroby. Oblicz prawdopodobieństwo tego, że pan
poddał się testowi, który dał wynik pozytywny. Pozytywny wynik oznacza podejrzenie choroby. Oblicz prawdopodobieństwo tego, że pan 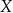 jest rzeczywiście chory. Wynik zapisz w postaci ułamka dziesiętnego w zaokrągleniu do części setnych.
jest rzeczywiście chory. Wynik zapisz w postaci ułamka dziesiętnego w zaokrągleniu do części setnych.
O zdarzeniach losowych 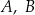 wiadomo, że:
wiadomo, że: 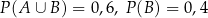 i
i 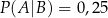 . Oblicz prawdopodobieństwo warunkowe
. Oblicz prawdopodobieństwo warunkowe 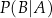 .
.
O zdarzeniach losowych 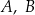 wiadomo, że:
wiadomo, że: 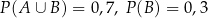 i
i 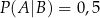 . Oblicz prawdopodobieństwo warunkowe
. Oblicz prawdopodobieństwo warunkowe 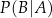 .
.
Z pojemnika zawierającego 10 kul białych i 6 czarnych losujemy jedną kulę i wkładamy zamiast niej jedną kulę czarną. Oblicz prawdopodobieństwo tego, że jeżeli teraz wylosujemy z pojemnika dwie kule, to obie wylosowane kule będą białe.
W każdej z dwóch urn jest tyle samo kul białych i czarnych, a trzecia urna jest pusta. Z każdej z dwóch pierwszych urn losujemy jedną kulę i wkładamy je do trzeciej urny. Następnie z trzeciej urny losujemy jedną kulę. Oblicz prawdopodobieństwo tego, że kula wylosowana z trzeciej urny jest biała.
W każdej z dwóch szuflad jest tyle samo rękawiczek prawych i lewych, a trzecia szuflada jest pusta. Z każdej z dwóch pierwszych szuflad losujemy jedną rękawiczkę i wkładamy je do trzeciej szuflady. Następnie z trzeciej szuflady losujemy jedną rękawiczkę. Oblicz prawdopodobieństwo tego, że rękawiczka wylosowana z trzeciej szuflady jest lewa.
W urnie znajduje się 5 kul białych i 3 czarne. Wyjmujemy losowo 4 kule. Oblicz prawdopodobieństwo, że wśród wyjętych są przynajmniej 2 kule czarne.
Ze zbioru 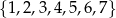 losujemy liczbę
losujemy liczbę  , a ze zbioru
, a ze zbioru 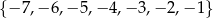 liczbę
liczbę 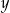 . Oblicz prawdopodobieństwo tego, że
. Oblicz prawdopodobieństwo tego, że 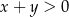 .
.
Ze zbioru 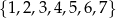 losujemy liczbę
losujemy liczbę  , a ze zbioru
, a ze zbioru 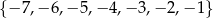 liczbę
liczbę 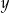 . Oblicz prawdopodobieństwo tego, że
. Oblicz prawdopodobieństwo tego, że 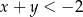 .
.
Ze zbioru 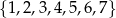 losujemy liczbę
losujemy liczbę  , a ze zbioru
, a ze zbioru 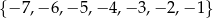 liczbę
liczbę 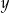 . Oblicz prawdopodobieństwo tego, że
. Oblicz prawdopodobieństwo tego, że 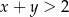 .
.
Ze zbioru liczb 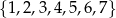 losujemy kolejno dwa razy po jednej liczbie bez zwracania. Oblicz prawdopodobieństwo zdarzenia
losujemy kolejno dwa razy po jednej liczbie bez zwracania. Oblicz prawdopodobieństwo zdarzenia 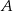 polegającego na tym, że pierwsza z wylosowanych liczb jest nieparzysta, a ich iloczyn jest większy od 10.
polegającego na tym, że pierwsza z wylosowanych liczb jest nieparzysta, a ich iloczyn jest większy od 10.
Ze zbioru liczb 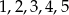 losujemy kolejno trzy razy po jednej liczbie bez zwracania tworząc liczbę trzycyfrową. Oblicz prawdopodobieństwo zdarzenia
losujemy kolejno trzy razy po jednej liczbie bez zwracania tworząc liczbę trzycyfrową. Oblicz prawdopodobieństwo zdarzenia 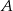 – otrzymana liczba jest mniejsza od 432.
– otrzymana liczba jest mniejsza od 432.
Ze zbioru liczb 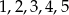 losujemy kolejno trzy razy po jednej liczbie bez zwracania tworząc liczbę trzycyfrową. Oblicz prawdopodobieństwo zdarzenia
losujemy kolejno trzy razy po jednej liczbie bez zwracania tworząc liczbę trzycyfrową. Oblicz prawdopodobieństwo zdarzenia  – otrzymana liczba jest większa od 324.
– otrzymana liczba jest większa od 324.
W pewnym liceum, wśród uczniów 30 osobowej klasy (każdy uczeń pochodzi z innej rodziny), zebrano dane na temat posiadanego rodzeństwa. Wyniki badań przedstawiono na diagramie.
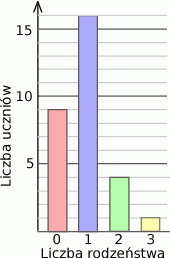
- Wychowawczyni wybrała 3 osoby z tej klasy. Oblicz prawdopodobieństwo, że jedna z nich ma dwoje rodzeństwa, a dwie pozostałe nie mają rodzeństwa. Wynik zaokrąglij do części setnych.
- Oblicz średnią liczbę dzieci w jednej badanej rodzinie, odchylenie standardowe i medianę.
Dane są trzy sześcienne kostki do gry: czerwona, niebieska i zielona. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że przy jednokrotnym rzucie trzema kostkami liczba otrzymana na niebieskiej kostce jest większa niż suma liczb otrzymanych na dwóch pozostałych kostkach.
Znając prawdopodobieństwa zdarzeń 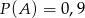 ,
, 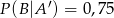 ,
, 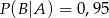 , gdzie
, gdzie 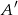 oznacza zdarzenie przeciwne do
oznacza zdarzenie przeciwne do 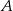 , oblicz prawdopodobieństwo zdarzenia
, oblicz prawdopodobieństwo zdarzenia 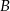 .
.
W pudełku znajdują się 4 kostki do gry: 3 sześcienne (ze ścianami ponumerowanymi liczbami od 1 do 6) i jedna czworościenna (ze ścianami ponumerowanymi liczbami od 1 do 4). Losowo wybrano kostkę, wykonano nią 3 rzuty i w wyniku tych 3 rzutów otrzymano trzy razy jedynkę. Jakie jest prawdopodobieństwo, że wybrana kostka była kostką czworościenną?
Ze zbioru liczb 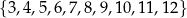 losujemy ze zwracaniem kolejno dwa razy po jednej liczbie. Oblicz prawdopodobieństwo zdarzenia
losujemy ze zwracaniem kolejno dwa razy po jednej liczbie. Oblicz prawdopodobieństwo zdarzenia  polegającego na tym, że iloczyn wylosowanych liczb jest podzielny przez 3.
polegającego na tym, że iloczyn wylosowanych liczb jest podzielny przez 3.
Losujemy dwa różne punkty spośród wierzchołków sześcianu o boku długości 1. Jakie jest prawdopodobieństwo, że
- odległość wylosowanych wierzchołków jest równa 1?
- odległość wylosowanych wierzchołków jest większa od
 ?
?

