Ze zbioru 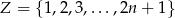 , gdzie
, gdzie 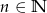 wylosowano równocześnie dwie liczby. Wyznacz
wylosowano równocześnie dwie liczby. Wyznacz  , tak aby prawdopodobieństwo wylosowania liczb, których suma jest liczbą nieparzystą było większe od
, tak aby prawdopodobieństwo wylosowania liczb, których suma jest liczbą nieparzystą było większe od 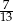 .
.
/Szkoła średnia/Prawdopodobieństwo
Rozmieszczamy 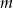 różnych listów w
różnych listów w 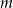 rozróżnialnych, ponumerowanych skrytkach. Jakie jest prawdopodobieństwo takiego rozmieszczenia, że:
rozróżnialnych, ponumerowanych skrytkach. Jakie jest prawdopodobieństwo takiego rozmieszczenia, że:
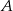 – co najmniej jedna skrytka jest pusta?
– co najmniej jedna skrytka jest pusta? 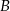 – co najmniej dwie skrytki są puste?
– co najmniej dwie skrytki są puste?
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo tego, że w każdym rzucie otrzymamy inną liczbę oczek.
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo tego, że iloczyn otrzymanych jest mniejszy od 25.
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo tego, że liczba oczek w każdym rzucie będzie parzysta lub większa od 3.
Doświadczenie losowe polega na dwukrotnym rzucie symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek – od jednego oczka do sześciu oczek. Oblicz prawdopodobieństwo zdarzenia 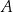 polegającego na tym, że w pierwszym rzucie wypadnie większa liczba oczek niż w drugim rzucie.
polegającego na tym, że w pierwszym rzucie wypadnie większa liczba oczek niż w drugim rzucie.
Rzucamy dwa razy symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek – od jednego oczka do sześciu oczek. Oblicz prawdopodobieństwo zdarzenia 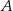 polegającego na tym, że co najmniej jeden raz wypadnie ścianka z pięcioma oczkami.
polegającego na tym, że co najmniej jeden raz wypadnie ścianka z pięcioma oczkami.
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo tego, że suma otrzymanych oczek jest równa co najmniej 5.
Rzucamy dwa razy symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek – od jednego oczka do sześciu oczek. Oblicz prawdopodobieństwo zdarzenia 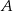 polegającego na tym, że co najwyżej jeden raz wypadnie ścianka z pięcioma oczkami.
polegającego na tym, że co najwyżej jeden raz wypadnie ścianka z pięcioma oczkami.
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo tego, że suma otrzymanych oczek jest równa co najmniej 4.
Oblicz prawdopodobieństwo, że w rzucie dwoma kostkami otrzymamy iloczyn oczek mniejszy od 11.
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo tego, że ani razu nie otrzymamy szóstki.
W dwóch pudełkach są cukierki. W pierwszym pudełku jest 15 cukierków czekoladowych i 5 owocowych, a w drugim pudełku jest 20 cukierków czekoladowych i 30 cukierków owocowych. Losujemy cukierek najpierw z pierwszego, a potem z drugiego pudełka. Jakie jest prawdopodobieństwo, że w wyniku losowania otrzymamy dwa cukierki czekoladowe?
W dwóch pudełkach są cukierki. W pierwszym pudełku jest 15 cukierków czekoladowych i 5 owocowych, a w drugim pudełku jest 20 cukierków czekoladowych i 30 cukierków owocowych. Losujemy cukierek najpierw z pierwszego, a potem z drugiego pudełka. Jakie jest prawdopodobieństwo, że jeden z wylosowanych cukierków będzie czekoladowy, a drugi owocowy?
Z talii 24 kart wyjęto losowo 1 kartę i odłożono na bok. Następnie wylosowano 2 karty. Oblicz prawdopodobieństwo, że za drugim razem wylosowano 2 kiery.
Rzucamy dziesięciokrotnie monetą. Wśród otrzymanych wyników dokładnie sześć razy otrzymaliśmy orła. Jakie jest prawdopodobieństwo, że w każdym z dwóch pierwszych rzutów otrzymaliśmy reszkę?
Prawdopodobieństwo tego, że z pewnej grupy osób wylosujemy osobę znającą język angielski jest równe 0,4, prawdopodobieństwo wylosowania osoby znającej język francuski jest równe 0,2, natomiast prawdopodobieństwo wylosowania osoby znającej oba te języki jest równe 0,1. Wykaż, że prawdopodobieństwo wylosowania osoby, która zna język angielski i nie zna języka francuskiego jest trzy razy większe od prawdopodobieństwa wylosowania osoby, która zna język francuski i nie zna języka angielskiego.
W jednej urnie są 3 kule: czerwona, biała i zielona, a w drugiej urnie są 2 kule: czerwona i biała. Losujemy po jednej kuli z każdej urny. Jakie jest prawdopodobieństwo wyciągnięcia dwóch kul w tym samym kolorze?
W jednej urnie są 4 kule: czerwona, biała, niebieska i zielona, a w drugiej urnie są 3 kule: czerwona, biała i zielona. Losujemy po jednej kuli z każdej urny. Jakie jest prawdopodobieństwo wyciągnięcia dwóch kul w tym samym kolorze?
W urnie jest pewna liczba kul białych i pewna liczba kul czarnych – razem 9 kul. Ile jest kul białych w urnie, jeśli wiadomo, że przy jednoczesnym losowaniu dwóch kul z tej urny prawdopodobieństwo otrzymania kul tego samego koloru jest równe prawdopodobieństwu otrzymania kul różnych kolorów?
Wśród 200 uczniów pewnego krakowskiego gimnazjum przeprowadzono ankietę dotyczącą planów wakacyjnych. Wyniki ankiety przedstawiono w tabeli.
| Klasa | Liczba uczniów | Liczba uczniów, którzy nie wyjadą na wakacje | Liczba uczniów, którzy wyjadą z rodzicami | Liczba uczniów, którzy wyjadą na kolonie |
| Pierwsza | 50 | 8 | 36 | 12 |
| Druga | 80 | 16 | 48 | 24 |
| Trzecia | 70 | 12 | 40 | 24 |
Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że losowo wybrana osoba, spośród ankietowanych, wyjedzie na wakacje, jeśli wiadomo, że ta osoba nie jest uczniem drugiej klasy.
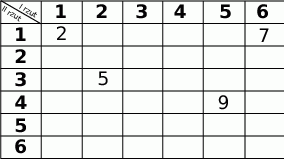
Rzucamy dwa razy symetryczną, sześcienną kostką do gry i zapisujemy sumę liczb wyrzuconych oczek.
- Uzupełnij tabelę, tak aby przedstawiała wszystkie możliwe wyniki tego doświadczenia.
- Oblicz prawdopodobieństwo zdarzenia
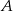 , polegającego na tym, że suma liczb oczek jest liczbą nieparzystą.
, polegającego na tym, że suma liczb oczek jest liczbą nieparzystą. - Oblicz prawdopodobieństwo zdarzenia
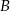 , polegającego na tym, że reszta z dzielenia sumy liczby oczek przez 3 jest równa 2.
, polegającego na tym, że reszta z dzielenia sumy liczby oczek przez 3 jest równa 2.
Wiadomo, że zdarzenia 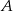 i
i 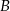 są niezależne oraz
są niezależne oraz 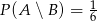 ,
, 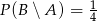 . Oblicz
. Oblicz 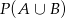 .
.
Ze zbioru 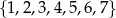 losujemy kolejno, bez zwracania trzy cyfry i tworzymy liczbę trzycyfrową: pierwsza wylosowana cyfra jest cyfrą setek, druga – cyfrą dziesiątek, a trzecia – cyfrą jedności. Oblicz prawdopodobieństwo zdarzenia, że otrzymana liczba ma następującą własność: różnica między największą i najmniejszą cyfrą tej liczby jest nie większa niż 3.
losujemy kolejno, bez zwracania trzy cyfry i tworzymy liczbę trzycyfrową: pierwsza wylosowana cyfra jest cyfrą setek, druga – cyfrą dziesiątek, a trzecia – cyfrą jedności. Oblicz prawdopodobieństwo zdarzenia, że otrzymana liczba ma następującą własność: różnica między największą i najmniejszą cyfrą tej liczby jest nie większa niż 3.
Z talii pięćdziesięciu dwu kart wyciągnięto losowo trzy karty. Oblicz prawdopodobieństwo wyciągnięcia dokładnie jednego króla.
Z talii pięćdziesięciu dwu kart wyciągnięto losowo trzy karty. Oblicz prawdopodobieństwo wyciągnięcia trzech kart jednego koloru.
Z talii pięćdziesięciu dwu kart wyciągnięto losowo trzy karty. Oblicz prawdopodobieństwo wyciągnięcia co najmniej dwóch króli.
Z talii pięćdziesięciu dwu kart wyciągnięto losowo trzy karty. Oblicz prawdopodobieństwo wyciągnięcia dokładnie jednej damy i dokładnie jednego króla.
Rzucamy cztery razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że suma kwadratów liczb oczek otrzymanych we wszystkich czterech rzutach będzie mniejsza niż 20.
Rozmieszczamy 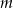 różnych listów w
różnych listów w 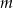 rozróżnialnych, ponumerowanych skrytkach. Jakie jest prawdopodobieństwo takiego rozmieszczenia, że dwa ustalone listy znalazły się w różnych skrytkach?
rozróżnialnych, ponumerowanych skrytkach. Jakie jest prawdopodobieństwo takiego rozmieszczenia, że dwa ustalone listy znalazły się w różnych skrytkach?
W sekretariacie stoją dwa telefony - biały i czarny. Telefony te dzwonią niezależnie od siebie. Prawdopodobieństwo, że w ciągu najbliższych pięciu minut zadzwoni telefon biały, jest równe 0,5. Prawdopodobieństwo, że w ciągu najbliższych pięciu minut zadzwoni telefon czarny, jest równe 0,4. Oblicz prawdopodobieństwo, że w ciągu najbliższych pięciu minut zadzwoni co najmniej jeden z telefonów.
Spośród wszystkich czterocyfrowych całkowitych liczb dodatnich losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana liczba będzie parzysta, a w jej zapisie dziesiętnym wystąpią dokładnie jedna cyfra 2 i dokładnie jedna cyfra 3.
Uzasadnij, że
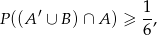
jeżeli 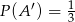 i
i 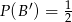 .
.
Losujemy jedną liczbę całkowitą z przedziału 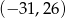 i jedną liczbę całkowitą z przedziału
i jedną liczbę całkowitą z przedziału 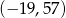 . Oblicz prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczb, których iloczyn jest dodatni. Wynik podaj w postaci ułamka nieskracalnego.
. Oblicz prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczb, których iloczyn jest dodatni. Wynik podaj w postaci ułamka nieskracalnego.
Losujemy jedną liczbę całkowitą z przedziału 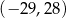 i jedną liczbę całkowitą z przedziału
i jedną liczbę całkowitą z przedziału 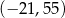 . Oblicz prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczb, których iloczyn jest ujemny. Wynik podaj w postaci ułamka nieskracalnego.
. Oblicz prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczb, których iloczyn jest ujemny. Wynik podaj w postaci ułamka nieskracalnego.

