Prawdopodobieństwo/Szkoła średnia - zadania z matematyki

/Szkoła średnia/Prawdopodobieństwo

Ze zbioru liczb 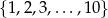{1,2,3,...,1 0} losujemy bez zwracania dwie i od pierwszej odejmujemy drugą. Oblicz prawdopodobieństwo, że otrzymana różnica jest większa od 2.

Ze zbioru liczb 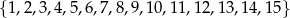{1,2 ,3 ,4,5,6,7,8,9,10,1 1,12,13,14,15 } losujemy bez zwracania dwa razy po jednej liczbie. Wylosowane liczby tworzą parę 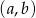(a ,b) , gdzie jest wynikiem pierwszego losowania, 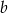jest wynikiem drugiego losowania. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że iloczyn 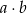a ⋅b jest liczbą parzystą.

Rzucono dwiema sześciennymi kostkami do gry i określono zdarzenia: 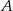– na każdej kostce wypadła inna liczba oczek, 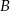– suma oczek jest mniejsza od 6. Oblicz prawdopodobieństwo zdarzenia A ∖ B .

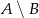Ze zbioru liczb 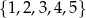{1,2,3,4 ,5} losujemy kolejno trzy razy po jednej liczbie ze zwracaniem tworząc liczbę trzycyfrową. Oblicz prawdopodobieństwo zdarzenia 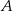– otrzymana liczba jest cztery razy większa od kwadratu liczby naturalnej.

W urnie znajduje się 20 kul: 9 białych, 9 czerwonych i 2 zielone. Z tej urny losujemy bez zwracania 3 kule. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że co najmniej dwie z wylosowanych kul są tego samego koloru.

Ukryj Podobne zadania

W urnie jest dziesięć kul różniących się wyłącznie kolorem: 4 czarne, 3 białe, 2 zielone i 1 niebieska. Losujemy jednocześnie trzy kule z urny. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że przynajmniej dwie z wylosowanych kul mają ten sam kolor.

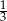W jednej urnie jest 5 kul białych i pewna liczba kul czarnych, w drugiej zaś 6 kul czarnych i pewna liczba kul białych. Z każdej urny losujemy po dwie kule. Prawdopodobieństwo wylosowania jednocześnie dwóch kul białych z pierwszej urny jest większe od 2 9 , a prawdopodobieństwo jednoczesnego wylosowania dwóch kul czarnych z drugiej urny jest większe od 1 3 . W której urnie jest więcej kul białych, a w której czarnych?

W każdym z dwóch pudełek znajduje się tyle samo kul. Kule te są w jednym z dwóch kolorów: czarne lub białe. Prawdopodobieństwo wylosowania kuli białej z pierwszego pudełka jest równe 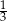i jest dwa razy większe niż prawdopodobieństwo wylosowania kuli czarnej z drugiego pudełka. Umieszczamy teraz wszystkie kule z tych dwóch pudełek w jednym trzecim pudełku. Jakie jest prawdopodobieństwo wylosowania kuli białej z trzeciego pudełka?

Wiedząc, że 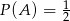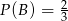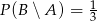1 P(A ) = 2 , 2 P(B ) = 3 , 1 P(B ∖ A ) = 3 , oblicz P(A ∖B ) .

Ukryj Podobne zadania

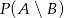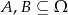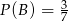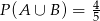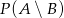Dane są zdarzenia losowe A ,B ⊆ Ω takie, że 3 P (B) = 7 i 4 P (A ∪ B ) = 5 . Oblicz P (A ∖ B) , gdzie zdarzenie 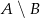A ∖B oznacza różnicę zdarzeń 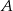i .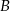

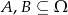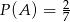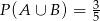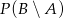Dane są zdarzenia losowe A ,B ⊆ Ω takie, że 2 P (A) = 7 i 3 P(A ∪ B) = 5 . Oblicz P (B ∖ A) , gdzie zdarzenie 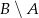B ∖ A oznacza różnicę zdarzeń 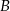i .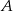

Spośród liczb: -9, -7, -5, -3, -1, 0, 2, 4, 6, 8 losujemy dwie różne liczby i 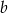, a następnie zapisujemy ich iloczyn 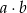a ⋅b . Oblicz i porównaj prawdopodobieństwa zdarzeń 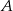i 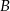, jeśli: 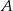oznacza zdarzenie, że iloczyn 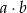a⋅ b jest liczbą nieujemną; 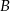– zdarzenie, że iloczyn 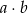a⋅b jest liczbą niedodatnią.

Wśród dziesięciu losów loteryjnych znajduje się jeden los z główną wygraną oraz dwa losy uprawniające do wylosowania następnego losu. Oblicz prawdopodobieństwo wygrania przy zakupie jednego losu.

Ze zbioru 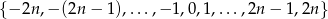{− 2n,− (2n − 1 ),...,− 1 ,0 ,1,...,2n − 1,2n} losujemy ze zwracaniem dwie liczby: i 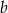. Rozważmy zdarzenia
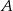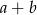: a + b jest liczbą parzystą;
: |a| + |b| ≤ 2n .
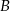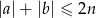Oblicz prawdopodobieństwo zdarzenia 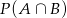P(A ∩ B) .

Z talii 52 kart losujemy jedną kartę.

Oblicz prawdopodobieństwo zdarzeń:
A – losowo wybrana karta jest pikiem.
B – losowo wybrana karta jest asem.
Oblicz prawdopodobieństwo zdarzeń 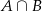oraz .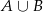

Rzucamy raz sześcienną kostką do gry, a następnie rzucamy tyloma monetami, ile oczek wypadło na kostce. Oblicz prawdopodobieństwo tego, że dokładnie na jednej z wyrzuconych monet jest reszka. Wynik podaj w postaci ułamka nieskracalnego.

Rzucamy dwukrotnie kostką, które ze zdarzeń jest bardziej prawdopodobne: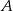
– w pierwszym rzucie otrzymamy liczbę oczek mniejszą niż w drugim;
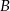– suma oczek, jakie wypadną w obydwu rzutach, jest nie mniejsza od 8?

Wśród 390 pracowników pewnej ﬁrmy jest 150 kobiet i 240 mężczyzn. Wśród nich w wieku przedemerytalnym jest 21 kobiet i 43 mężczyzn. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że losowo wybrany pracownik tej ﬁrmy jest w wieku przedemerytalnym – pod warunkiem że jest mężczyzną.

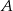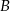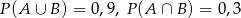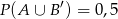O zdarzeniach losowych i wiadomo, że P (A ∪ B) = 0,9, P (A ∩ B ) = 0,3 i P (A ∪ B ′) = 0 ,5 . Oblicz P (A ′ ∪ B ) .

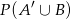Dany jest zbiór 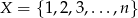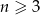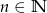X = {1,2,3 ,...,n } , n ≥ 3 , n ∈ N . Ze zbioru 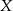losujemy kolejno bez zwracania dwie liczby. Oblicz prawdopodobieństwo, że pierwsza z wylosowanych liczb jest większa od drugiej.

Zakupiono 16 biletów do teatru, w tym 10 biletów na miejsca od 1. do 10. w pierwszym rzędzie i 6 biletów na miejsca od 11. do 16. w szesnastym rzędzie. Jakie jest prawdopodobieństwo zdarzenia polegającego na tym, że 2 wylosowane bilety, spośród szesnastu, będą biletami na sąsiadujące miejsca?

Z trzech urn, w których jest po 2 kule białe i 3 czarne, wyjmujemy po jednej kuli i wkładamy do czwartej urny, w której była jedna kula biała. Losujemy teraz jedną kulę z czwartej urny. Oblicz prawdopodobieństwo, że z czwartej urny wyjmiemy białą kulę.

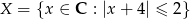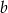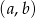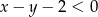Ze zbioru X = {x ∈ C : |x + 4| ≤ 2} losujemy dwa razy (bez zwracania) po jednej liczbie. Oznaczamy te liczby w kolejności losowania przez oraz . Oblicz prawdopodobieństwo tego, że wylosowana para liczb (a,b) jest rozwiązaniem nierówności x − y − 2 < 0 .

Strona 8 z 22