Grupa 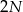 chłopców i
chłopców i 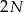 dziewcząt podzieliła się losowo na 2 równoliczne grupy. Jakie jest prawdopodobieństwo, że w każdej z tych grup jest tyle samo chłopców co dziewcząt?
dziewcząt podzieliła się losowo na 2 równoliczne grupy. Jakie jest prawdopodobieństwo, że w każdej z tych grup jest tyle samo chłopców co dziewcząt?
/Szkoła średnia/Prawdopodobieństwo
Doświadczenie losowe polega na tym, że losujemy bez zwracania trzy liczby ze zbioru 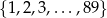 . Oblicz prawdopodobieństwo, że wśród wylosowanych liczb jest liczba parzysta, jeżeli wiadomo, że pierwsza z wylosowanych liczb jest nieparzysta.
. Oblicz prawdopodobieństwo, że wśród wylosowanych liczb jest liczba parzysta, jeżeli wiadomo, że pierwsza z wylosowanych liczb jest nieparzysta.
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo każdego z następujących zdarzeń:
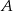 — w każdym rzucie wypadnie nieparzysta liczba oczek.
— w każdym rzucie wypadnie nieparzysta liczba oczek. 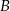 -– suma oczek otrzymanych w obu rzutach jest liczbą większą od 9.
-– suma oczek otrzymanych w obu rzutach jest liczbą większą od 9. 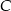 -– suma oczek otrzymanych w obu rzutach jest liczbą nieparzystą i większą od 9.
-– suma oczek otrzymanych w obu rzutach jest liczbą nieparzystą i większą od 9.
Maszyna napełnia torebki herbatą. Każda torebka ma zostać napełniona 200 g herbaty. Torebkę, która zawiera mniej niż 200 g herbaty, nazywamy torebką z niedowagą. Prawdopodobieństwo tego, że pojedyncza torebka napełniona przez tę maszynę jest z niedowagą, jest równe 0,1. Kontroli poddano masę herbaty w torebkach napełnianych przez tę maszynę danego dnia. Do kontroli wybrano losowo 20 torebek. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wśród tych 20 losowo wybranych torebek znajdą się co najwyżej dwie torebki z niedowagą.
Maszyna napełnia butelki wodą, przy czym każda butelka ma zostać napełniona wodą do 750 ml objętości. Prawdopodobieństwo tego, że butelka zostanie napełniona prawidłowo wynosi 97%. Kontroli poddano partię 30 butelek napełnionych przez tę maszynę danego dnia. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wśród tych 30 losowo wybranych butelek znajdą się co najwyżej dwie butelki, które nie zostały prawidłowo napełnione.
W pewnym zakładzie mleczarskim śmietana produkowana jest w 200–gramowych opakowaniach. Prawdopodobieństwo zdarzenia, że w losowo wybranym opakowaniu śmietana zawiera mniej niż 36% tłuszczu, jest równe 0,01. Kontroli poddajemy 10 losowo wybranych opakowań ze śmietaną. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wśród opakowań poddanych tej kontroli będzie co najwyżej jedno opakowanie ze śmietaną, która zawiera mniej niż 36% tłuszczu. Wynik zapisz w postaci ułamka dziesiętnego w zaokrągleniu do części tysięcznych.
W każdej z czterech urn są 24 kule, w tym dokładnie 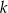 białych. Z każdej urny losujemy jedną kulę. Dla jakiej wartości
białych. Z każdej urny losujemy jedną kulę. Dla jakiej wartości 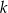 prawdopodobieństwo wylosowania dokładnie dwóch kul białych jest największe? Oblicz to największe prawdopodobieństwo.
prawdopodobieństwo wylosowania dokładnie dwóch kul białych jest największe? Oblicz to największe prawdopodobieństwo.
W pojemniku znajduje się 200 wybrakowanych części. 60 sztuk odrzucono z powodu wystąpienia wady 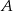 , 40 sztuk z powodu wady
, 40 sztuk z powodu wady 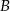 , pozostałe z powodu wady
, pozostałe z powodu wady 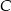 . Każda część ma tylko jedną wadę. Oblicz prawdopodobieństwo, że wybierając losowo z tego pojemnika 3 części, wybierzesz dokładnie po jednej części z każdą z wad.
. Każda część ma tylko jedną wadę. Oblicz prawdopodobieństwo, że wybierając losowo z tego pojemnika 3 części, wybierzesz dokładnie po jednej części z każdą z wad.
W pojemniku znajduje się 200 wybrakowanych części. 60 sztuk odrzucono z powodu wystąpienia wady 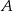 , 40 sztuk z powodu wady
, 40 sztuk z powodu wady 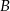 , pozostałe z powodu wady
, pozostałe z powodu wady 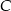 . Każda część ma tylko jedną wadę. Oblicz prawdopodobieństwo, że wybierając losowo z tego pojemnika 3 części, wybierzesz dokładnie dwie części z wadą
. Każda część ma tylko jedną wadę. Oblicz prawdopodobieństwo, że wybierając losowo z tego pojemnika 3 części, wybierzesz dokładnie dwie części z wadą 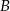 .
.
W pojemniku znajduje się 200 wybrakowanych części. 60 sztuk odrzucono z powodu wystąpienia wady 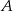 , 40 sztuk z powodu wady
, 40 sztuk z powodu wady 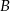 , pozostałe z powodu wady
, pozostałe z powodu wady 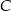 . Każda część ma tylko jedną wadę. Oblicz prawdopodobieństwo, że wybierając losowo z tego pojemnika 3 części, wybierzesz dokładnie dwie części z wadą
. Każda część ma tylko jedną wadę. Oblicz prawdopodobieństwo, że wybierając losowo z tego pojemnika 3 części, wybierzesz dokładnie dwie części z wadą 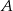 .
.
W pojemniku znajduje się 200 wybrakowanych części. 60 sztuk odrzucono z powodu wystąpienia wady 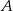 , 40 sztuk z powodu wady
, 40 sztuk z powodu wady 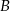 , pozostałe z powodu wady
, pozostałe z powodu wady 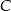 . Każda część ma tylko jedną wadę. Oblicz prawdopodobieństwo, że wybierając losowo z tego pojemnika 3 części, wybierzesz wszystkie części z tą samą jedną wadą.
. Każda część ma tylko jedną wadę. Oblicz prawdopodobieństwo, że wybierając losowo z tego pojemnika 3 części, wybierzesz wszystkie części z tą samą jedną wadą.
W jadalni znajduje się okrągły stół, przy którym może usiąść 6 osób. Pod ścianą stoi ława, na której również może usiąść 6 osób. Do jadalni wchodzi 6 osób, które najpierw w sposób losowy siadają przy stole, a następnie na ławie. Które z prawdopodobieństw jest większe: prawdopodobieństwo tego, że 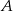 i
i 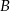 będą sąsiadami, siadając przy stole, czy prawdopodobieństwo tego, że
będą sąsiadami, siadając przy stole, czy prawdopodobieństwo tego, że 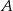 i
i 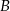 będą sąsiadami, siadając na ławie?
będą sąsiadami, siadając na ławie?
Oblicz prawdopodobieństwo, że w rzucie pięcioma sześciennymi kostkami do gry otrzymamy sumę oczek różną od 28.
Do woreczka wrzucono 3 monety 5 złotowe, 4 monety 2 złotowe, 2 monety 1 złotowe oraz 8 monet 50 groszowych. Karol losowo wyjmuje z woreczka 10 monet. Jakie jest prawdopodobieństwo, że wylosuje w ten sposób co najmniej 10 zł? Wynik podaj z dokładnością do trzech miejsc po przecinku.
Wśród uczniów pewnej szkoły przeprowadzono ankietę dotyczącą posiadanego rodzeństwa i okazało się, że:
– prawdopodobieństwo, że losowo wybrany uczeń ma brata jest równe 0,6;
– jeżeli wybierzemy losowo ucznia, który ma brata, to prawdopodobieństwo, że ten uczeń ma również siostrę jest równe 0,3;
– jeżeli wybierzemy losowo ucznia, który ma brata i ma siostrę, to prawdopodobieństwo, że ten uczeń jest uczniem klasy pierwszej jest równe 0,4.
Oblicz jakie jest prawdopodobieństwo, że losowo wybrany uczeń tej szkoły jest uczniem klasy pierwszej, który ma brata i siostrę.
Z cyfr 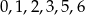 tworzymy liczbę czterocyfrową, przy czym cyfry nie mogą się powtarzać. Jakie jest prawdopodobieństwo otrzymania liczby podzielnej przez 25?
tworzymy liczbę czterocyfrową, przy czym cyfry nie mogą się powtarzać. Jakie jest prawdopodobieństwo otrzymania liczby podzielnej przez 25?
Na jednej kostce sześciennej znajdują się liczby: 2,3,3,6,6,6, a na drugiej: 1,1,4,6,7,7. Gra polega na rzucie wybraną kostką. Wygrywa ten, kto wyrzuci większą liczbę na swojej kostce. Masz prawo wyboru kostki. Którą kostkę należy wybrać, aby mieć większe szanse wygranej?
Zamek szyfrowy składa się z 5 tarcz. Na każdej z tarcz znajduje się 6 cyfr. Zamek otwiera kombinacja cyfr podana w odpowiedniej kolejności. (istotne są cyfry na tarczach oraz kolejność ustawiania tarcz). Jakie jest prawdopodobieństwo otworzenia zamka przy losowym ustawieniu tarcz?
W klasach 3a, 3b i 3c przeprowadzono sprawdzian. Losowo wybieramy klasę, a następnie ucznia z tej klasy. Jakie jest prawdopodobieństwo, że wybrany uczeń otrzymał ocenę co najmniej 4, jeżeli wiadomo, że
w klasie 3a: wszystkich uczniów jest 20, uczniów z oceną co najmiej cztery jest 8;
w klasie 3b: wszystkich uczniów jest 21, uczniów z oceną co najmiej cztery jest 14;
w klasie 3c: wszystkich uczniów jest 18, uczniów z oceną co najmiej cztery jest 6.
Ze zbioru 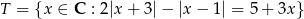 losujemy 3 liczby
losujemy 3 liczby 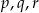 ze zwracaniem i tworzymy funkcję
ze zwracaniem i tworzymy funkcję 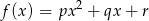 . Oblicz prawdopodobieństwa zdarzeń:
. Oblicz prawdopodobieństwa zdarzeń:
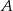 – otrzymana funkcja jest parzysta.
– otrzymana funkcja jest parzysta. 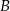 – otrzymana funkcja jest różnowartościowa.
– otrzymana funkcja jest różnowartościowa. 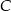 – otrzymana funkcja jest stała.
– otrzymana funkcja jest stała.
Ze zbioru 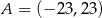 losujemy dwucyfrową liczbę całkowitą
losujemy dwucyfrową liczbę całkowitą  , natomiast ze zbioru
, natomiast ze zbioru 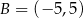 losujemy liczbę całkowitą
losujemy liczbę całkowitą 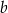 . Te liczby są współczynnikami funkcji
. Te liczby są współczynnikami funkcji 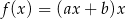 . Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wykres otrzymanej funkcji
. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wykres otrzymanej funkcji 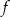 ma co najmniej dwa punkty wspólne z prostą
ma co najmniej dwa punkty wspólne z prostą 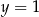 .
.
Niech 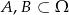 będą zdarzeniami losowymi, takimi że
będą zdarzeniami losowymi, takimi że 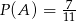 i
i 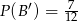 . Uzasadnij, że
. Uzasadnij, że 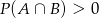 .
.
W jednej szufladzie znajdują się 3 szaliki czarne i 4 szaliki niebieskie, a w drugiej szufladzie są 2 czapki czarne i 1 niebieska. Wyjmujemy losowo jeden szalik i jedną czapkę. Które prawdopodobieństwo jest większe: zdarzenia 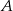 , że otrzymamy komplet w jednym kolorze, czy zdarzenia
, że otrzymamy komplet w jednym kolorze, czy zdarzenia 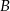 , że otrzymamy czapkę i szalik w różnych kolorach? Odpowiedź uzasadnij, wykonując odpowiednie obliczenia.
, że otrzymamy czapkę i szalik w różnych kolorach? Odpowiedź uzasadnij, wykonując odpowiednie obliczenia.
W każdym z dwóch koszyków znajduje się 5 klocków czerwonych, 10 zielonych i 6 białych. Wyjmujemy losowo po jednym klocku z każdego koszyka. Oblicz prawdopodobieństwo, że:
- wylosujemy dwa klocki białe;
- wylosujemy klocki tego samego koloru.
W dwóch urnach znajdują się kule białe i czarne, przy czym w pierwszej jest 6 kul białych i 4 czarne, a w drugiej urnie 5 białych i 5 czarnych. Rzucamy raz symetryczną kostką do gry. Jeżeli wyrzucimy co najmniej 4 oczka to losujemy 2 kule z pierwszej urny, a jeżeli wyrzucimy co najwyżej 3 oczka to losujemy 2 kule z drugiej urny. Oblicz prawdopodobieństwo wylosowania dwóch kul białych.

