Prawdopodobieństwo/Szkoła średnia - zadania z matematyki

/Szkoła średnia/Prawdopodobieństwo

Oblicz prawdopodobieństwo, że w trzech rzutach symetryczną sześcienną kostką do gry suma kwadratów liczb wyrzuconych oczek będzie podzielna przez 4.

10 kul rozmieszczamy w 10 szuﬂadach. Jakie jest prawdopodobieństwo tego, że każda szuﬂada będzie zajęta?

Dla zdarzeń 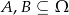A ,B ⊆ Ω spełnione są warunki 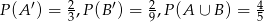′ 2 ′ 2 4 P (A ) = 3,P (B ) = 9 ,P (A ∪ B ) = 5 . Oblicz P (A ∩ B ) .

Ukryj Podobne zadania

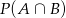Zdarzenia 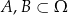A ,B ⊂ Ω spełniają warunki 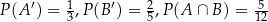′ 1 ′ 2 5- P(A ) = 3,P (B ) = 5,P (A ∩ B ) = 12 . Wyznacz P (A ∪ B) .

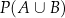Liczba uczniów w klasie jest 812 razy mniejsza od liczby utworzonych z nich uporządkowanych trójek. Oblicz prawdopodobieństwo wylosowania trzech osób, które (w kolejności losowania) są zapisane w dzienniku pod numerami pierwszym, drugim, i trzecim.

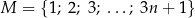Niech będzie ustaloną liczbą naturalną dodatnią. Ze zbioru M = {1; 2; 3; ...; 3n+ 1} losujemy jednocześnie trzy liczby. Zdarzenie 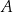odpowiada jednoczesnemu wylosowaniu ze zbioru 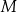trzech liczb, których suma przy dzieleniu przez 3 daje resztę 1. Oblicz prawdopodobieństwo zdarzenia .

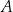Ze zbioru 99 kolejnych liczb naturalnych – od 1 do 99 – losujemy kolejno bez zwracania dwa razy po jednej liczbie. Niech 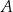oznacza zdarzenie polegające na tym, że suma wylosowanych liczb jest liczbą parzystą. Oblicz prawdopodobieństwo zdarzenia .

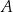Rzucamy dwiema sześciennymi kostkami.

Jakie jest prawdopodobieństwo, że różnica między liczbami oczek wyrzuconych na kostkach (od większej odejmujemy mniejszą) będzie równa 2?
Jaka jest najbardziej prawdopodobna różnica między wynikami na kostkach (od większego odejmujemy mniejszy)?

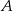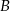O zdarzeniach i wiadomo, że 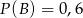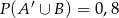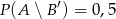P (B) = 0,6 , ′ P (A ∪ B) = 0,8 , P (A ∖ B′) = 0,5 . Oblicz prawdopodobieństwo zdarzenia .

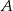Z talii 52 kart wylosowano dwie karty i, nie oglądając ich, włożono do drugiej talii. W ten sposób powstała talia złożona z 54 kart. Oblicz prawdopodobieństwo wylosowania asa z tak utworzonej talii kart.

Wiadomo, że 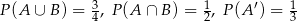3 1 ′ 1 P (A ∪ B ) = 4, P(A ∩ B ) = 2, P(A ) = 3 . Oblicz prawdopodobieństwa zdarzeń 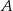i .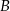

Rzucamy trzema kostkami. Prawdopodobieństwo otrzymania sumy oczek równej 3 wynosi 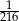1216- , a prawdopodobieństwo otrzymania sumy oczek równej 4 wynosi 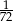-1 72 . jakie jest prawdopodobieństwo tego, że suma otrzymanych oczek będzie mniejsza od 5?

Na loterię przygotowano 30 losów, z których jest wygrywających. Kupujemy 2 razy po jednym losie. Wyznacz , jeśli wiadomo, że prawdopodobieństwo kupienia w ten sposób dwóch losów wygrywających jest równe 219 .

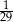Przy okrągłym stole zasiada losowo 8 osób, a wśród nich rodzice z dwojgiem dzieci. Jakie jest prawdopodobieństwo tego, że dzieci usiądą bezpośrednio między rodzicami?

Rzucamy cztery razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że iloczyn liczb oczek otrzymanych we wszystkich czterech rzutach będzie równy 60 .

W pewnej grupie uczniów każdy zna język angielski lub niemiecki. Wiadomo, że prawdopodobieństwo wylosowania z tej grupy ucznia znającego język angielski jest równe , natomiast prawdopodobieństwo wylosowania ucznia znającego język niemiecki jest równe 4 5 . Jakie jest prawdopodobieństwo tego, że losowo wybrany uczeń zna obydwa języki?

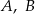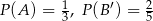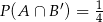O zdarzeniach losowych A , B wiadomo, że: 1 ′ 2 P(A ) = 3, P(B ) = 5 i P (A ∩ B ′) = 14 . Oblicz prawdopodobieństwo warunkowe P(A |B) .

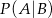Z talii 52 kart wyciągamy losowo jedną. Oblicz prawdopodobieństwo, że wyciągnięta karta będzie damą lub treﬂem.

Ukryj Podobne zadania

Z talii 52 kart wyciągamy losowo jedną. Oblicz prawdopodobieństwo, że wyciągnięta karta będzie królem, asem lub kierem.

Rzucono 8 razy monetą. Oblicz prawdopodobieństwo tego, że co najmniej jeden raz wyrzucono orła.

Ukryj Podobne zadania

Rzucono 8 razy monetą. Oblicz prawdopodobieństwo tego, że dokładnie jeden raz wyrzucono orła.

Spośród wszystkich liczb naturalnych sześciocyfrowych, których wszystkie cyfry należą do zbioru 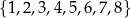{ 1,2,3,4,5,6,7,8} , losujemy jedną. Wylosowanie każdej z tych liczb jest jednakowo prawdopodobne. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy liczbę, która ma następującą własność: kolejne cyfry tej liczby (licząc od lewej strony) tworzą – w podanej kolejności – sześciowyrazowy ciąg malejący.

W magazynie są dwie równe partie elementów produkowanych w fabrykach I i II. Niezawodność (w czasie 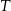) elementów z fabryki I jest równa 0,9, a z fabryki II 0,7. W sposób przypadkowy wzięto jeden element z magazynu i okazało się, że był sprawny przez czas 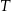. Obliczyć prawdopodobieństwo, że wybrany element pochodzi z fabryki I.

Strona 6 z 22