Udowodnij że jeśli dwie dwusieczne w trójkącie są sobie równe to trójkąt jest równoramienny (twierdzenie Steinera-Lehmusa).
/Konkursy/Zadania/Geometria
Dwa okręgi przecinają się w punktach 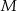 i
i 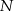 . Przez punkt
. Przez punkt 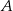 pierwszego okręgu prowadzimy proste
pierwszego okręgu prowadzimy proste 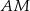 i
i 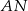 , przecinające drugi okrąg w punktach
, przecinające drugi okrąg w punktach 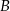 i
i 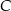 . Udowodnij, że styczna w punkcie
. Udowodnij, że styczna w punkcie 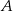 do pierwszego okręgu jest równoległa do prostej
do pierwszego okręgu jest równoległa do prostej 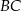 .
.
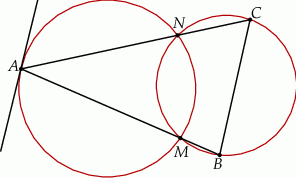
Dwa okręgi przecinają się w punktach 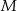 i
i 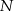 . Przez punkt
. Przez punkt 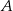 pierwszego okręgu prowadzimy proste
pierwszego okręgu prowadzimy proste 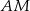 i
i 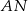 , przecinające drugi okrąg w punktach
, przecinające drugi okrąg w punktach 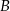 i
i 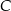 . Udowodnij, że styczna w punkcie
. Udowodnij, że styczna w punkcie 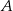 do pierwszego okręgu jest równoległa do prostej
do pierwszego okręgu jest równoległa do prostej 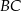 .
.
Wyznacz miary kątów trójkąta, w którym wysokość i środkowa poprowadzona z jednego wierzchołka dzielą kąt przy tym wierzchołku na 3 równe części.
Obwód trójkąta 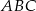 jest równy 8. Oblicz obwód trójkąta
jest równy 8. Oblicz obwód trójkąta 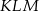 o wierzchołkach będących środkami środkowych trójkąta
o wierzchołkach będących środkami środkowych trójkąta 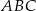 .
.
W pewnym trapezie kąty przy dwóch przeciwległych wierzchołkach mają miary  oraz
oraz 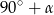 . Jedno z ramion tego trapezu ma długość
. Jedno z ramion tego trapezu ma długość 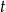 . Wyznacz różnicę długości podstaw tego trapezu.
. Wyznacz różnicę długości podstaw tego trapezu.
Podstawy trapezu 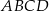 mają długości
mają długości 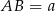 i
i 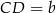 . Oblicz długość odcinka łączącego środki ramion trapezu.
. Oblicz długość odcinka łączącego środki ramion trapezu.
Dany jest czworokąt wypukły 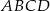 niebędący równoległobokiem. Punkty
niebędący równoległobokiem. Punkty 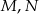 są odpowiednio środkami boków
są odpowiednio środkami boków 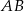 i
i 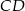 . Punkty
. Punkty 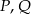 są odpowiednio środkami przekątnych
są odpowiednio środkami przekątnych 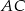 i
i 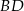 . Uzasadnij, że jeżeli odcinki
. Uzasadnij, że jeżeli odcinki 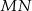 i
i 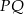 są prostopadłe, to
są prostopadłe, to 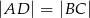 .
.
Wykaż, że jeżeli odcinki łączące środki przeciwległych boków czworokąta są prostopadłe, to przekątne tego czworokąta mają równe długości.
Punkt 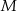 przyprostokątnej
przyprostokątnej 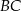 trójkąta prostokątnego
trójkąta prostokątnego 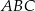 zrzutowano na przeciwprostokątną
zrzutowano na przeciwprostokątną 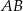 otrzymując punkt
otrzymując punkt 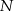 . Wykaż, że
. Wykaż, że 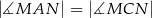 .
.
Dwusieczna kąta 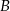 trójkąta
trójkąta 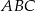 przecina bok
przecina bok 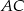 w punkcie
w punkcie 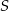 , a dwusieczna kąta
, a dwusieczna kąta 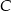 przecina bok
przecina bok 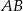 w punkcie
w punkcie 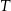 . Dwusieczne przecinają się w punkcie
. Dwusieczne przecinają się w punkcie 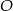 . Znajdź miarę kąta
. Znajdź miarę kąta 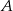 , jeżeli wiadomo, że na czworokącie
, jeżeli wiadomo, że na czworokącie 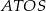 można opisać okrąg.
można opisać okrąg.
Dany jest równoległobok 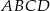 . Okrąg wpisany w trójkąt
. Okrąg wpisany w trójkąt 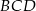 jest styczny do przekątnej
jest styczny do przekątnej 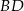 w punkcie
w punkcie 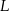 , a okrąg wpisany w trójkąt
, a okrąg wpisany w trójkąt 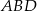 ma środek
ma środek 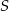 i jest styczny do boku
i jest styczny do boku 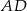 w punkcie
w punkcie  .
.
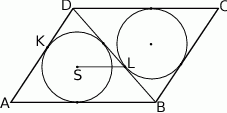
Wykaż, że jeżeli odcinek 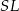 jest równoległy do prostej
jest równoległy do prostej  , to
, to 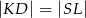 .
.
Dane są cztery okręgi. Każdy z nich jest styczny zewnętrznie do dokładnie dwóch spośród trzech pozostałych okręgów. Udowodnij, że punkty styczności tych okręgów są wierzchołkami czworokąta, na którym można opisać okrąg.
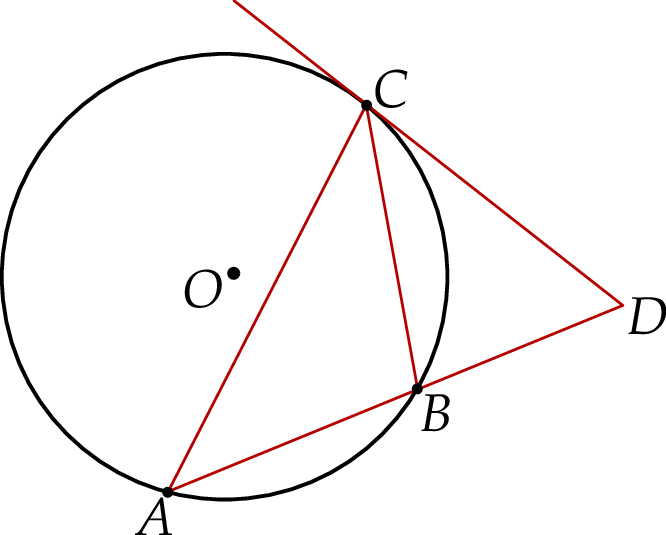
Prosta 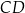 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 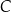 . Uzasadnij, że jeśli
. Uzasadnij, że jeśli 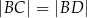 , to
, to 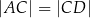 .
.
Na bokach 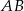 i
i 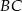 trójkąta ostrokątnego
trójkąta ostrokątnego 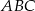 opisano, jako na średnicach, dwa okręgi. Gdzie leży punkt przecięcia się tych okręgów (różny od punktu B)?
opisano, jako na średnicach, dwa okręgi. Gdzie leży punkt przecięcia się tych okręgów (różny od punktu B)?
Cztery miasta 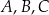 i
i 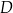 znajdują się w wierzchołkach kwadratu o boku 300 km. Pewna firma dostała zlecenie na zaprojektowanie sieci dróg, która będzie łączyć każde dwa z tych miast. Sieć ma posiadać dwa węzły, a łączna długość dróg w sieci ma być możliwie najmniejsza. Jeden z węzłów ma ma być połączony z miastami
znajdują się w wierzchołkach kwadratu o boku 300 km. Pewna firma dostała zlecenie na zaprojektowanie sieci dróg, która będzie łączyć każde dwa z tych miast. Sieć ma posiadać dwa węzły, a łączna długość dróg w sieci ma być możliwie najmniejsza. Jeden z węzłów ma ma być połączony z miastami 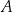 i
i  , a drugi węzeł z miastami
, a drugi węzeł z miastami  i
i  (zobacz rysunek).
(zobacz rysunek).
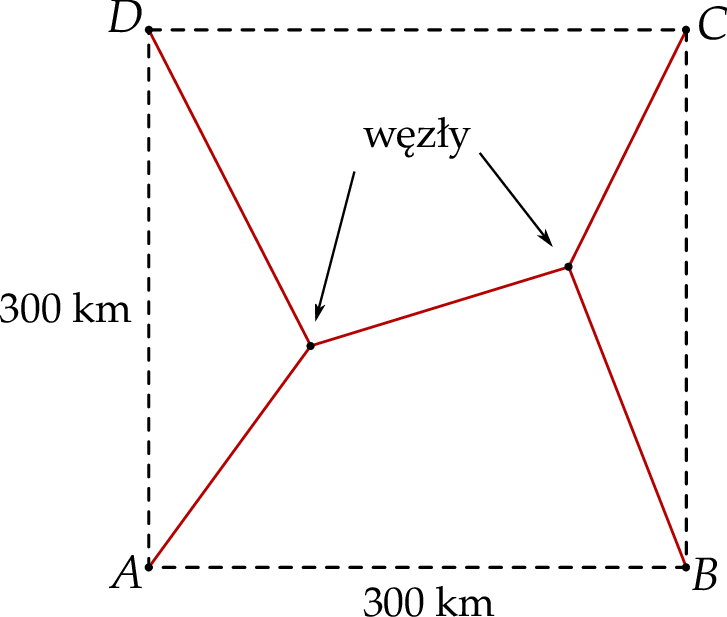
Oblicz, jaka musi być długość najkrótszej takiej sieci dróg i gdzie muszą być zlokalizowane węzły tej sieci.
Przekątne trapezu przecinają się w punkcie 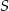 . Przez punkt
. Przez punkt 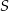 poprowadzono prostą równoległą do podstaw trapezu, która przecina ramiona trapezu w punktach
poprowadzono prostą równoległą do podstaw trapezu, która przecina ramiona trapezu w punktach 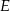 i
i 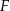 . Wykaż, że
. Wykaż, że 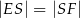 .
.
W trapezie 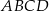 o podstawach
o podstawach 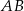 i
i 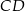 przez punkt
przez punkt 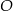 przecięcia się przekątnych poprowadzono dwie proste równoległe do boków
przecięcia się przekątnych poprowadzono dwie proste równoległe do boków 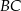 i
i 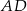 . Prosta równoległa do boku
. Prosta równoległa do boku 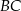 przecina bok
przecina bok 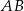 w punkcie
w punkcie 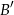 , a prosta równoległa do boku
, a prosta równoległa do boku 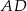 przecina bok
przecina bok 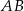 w punkcie
w punkcie 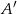 . Wykaż, że
. Wykaż, że 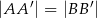 .
.
W kwadrat 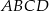 o boku długości
o boku długości 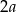 wpisano okrąg. Oblicz długość cięciwy wyciętej przez ten okrąg z odcinka łączącego wierzchołek
wpisano okrąg. Oblicz długość cięciwy wyciętej przez ten okrąg z odcinka łączącego wierzchołek 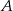 ze środkiem boku
ze środkiem boku 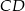 .
.
W trójkąt 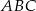 , w którym
, w którym 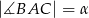 oraz
oraz 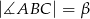 , wpisano okrąg. Punkty
, wpisano okrąg. Punkty 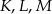 są punktami styczności okręgu odpowiednio z bokami
są punktami styczności okręgu odpowiednio z bokami 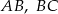 i
i 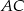 . Wykaż, że
. Wykaż, że 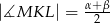 .
.
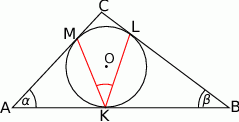
W półkole o średnicy 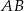 wpisano okrąg styczny do średnicy
wpisano okrąg styczny do średnicy 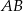 w jej środku. Znajdź promień okręgu stycznego jednocześnie do półokręgu
w jej środku. Znajdź promień okręgu stycznego jednocześnie do półokręgu 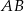 , do wpisanego okręgu oraz do średnicy
, do wpisanego okręgu oraz do średnicy 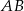 jeżeli
jeżeli 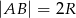 .
.
Dwa okręgi przecinają się w punktach 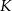 i
i 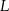 . Przez punkty
. Przez punkty 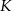 i
i 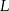 poprowadzono proste, które przecinają dane okręgi w punktach
poprowadzono proste, które przecinają dane okręgi w punktach 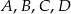 tak, jak pokazano to na poniższym rysunku. Wykaż, że
tak, jak pokazano to na poniższym rysunku. Wykaż, że 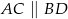 .
.
Udowodnij, że w trapezie, który ma dwa kąty ostre przy jednej z podstaw, suma kwadratów przekątnych równa jest sumie podwojonego iloczynu dwóch boków równoległych i kwadratów pozostałych boków.

