Dwa okręgi o promieniach  i
i 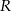 (
(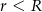 ) są styczne zewnętrznie. Prosta
) są styczne zewnętrznie. Prosta 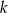 nie przechodzi przez punkt wspólny tych okręgów i jest styczna do każdego z nich. Znajdź promień okręgu stycznego zewnętrznie do danych okręgów i stycznego do prostej
nie przechodzi przez punkt wspólny tych okręgów i jest styczna do każdego z nich. Znajdź promień okręgu stycznego zewnętrznie do danych okręgów i stycznego do prostej 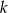 . Rozważ dwa przypadki.
. Rozważ dwa przypadki.
/Konkursy/Zadania/Geometria
Dane są dwa kąty wpisane oparte na tym samym łuku. Wykaż, że dwusieczne tych kątów przetną się w punkcie należącym do okręgu.
Pole trapezu jest równe 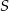 , a stosunek długości jego podstaw wynosi
, a stosunek długości jego podstaw wynosi 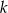 . Przekątne dzielą trapez na cztery trójkąty. Oblicz pole każdego z tych trójkątów.
. Przekątne dzielą trapez na cztery trójkąty. Oblicz pole każdego z tych trójkątów.
W kole o środku 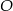 poprowadzono dwie prostopadłe średnice
poprowadzono dwie prostopadłe średnice 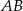 i
i 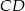 oraz cięciwę
oraz cięciwę 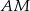 przecinającą średnicę
przecinającą średnicę 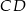 w punkcie
w punkcie 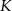 . Oblicz miarę kąta
. Oblicz miarę kąta 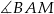 wiedząc, że w czworokąt
wiedząc, że w czworokąt 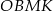 można wpisać okrąg.
można wpisać okrąg.
W trójkącie 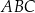 dwusieczna kąta
dwusieczna kąta 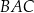 przecina bok
przecina bok 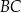 trójkąta w punkcie
trójkąta w punkcie 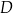 . Wykaż, że
. Wykaż, że
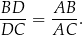
Trójkąty 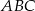 i
i 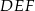 wpisano w ten sam okrąg. Udowodnij, że równość obwodów tych trójkątów jest równoważna równości sum sinusów ich kątów wewnętrznych.
wpisano w ten sam okrąg. Udowodnij, że równość obwodów tych trójkątów jest równoważna równości sum sinusów ich kątów wewnętrznych.
Dany jest trójkąt 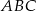 , w którym
, w którym 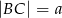 . Z wierzchołka
. Z wierzchołka 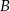 poprowadzono środkową
poprowadzono środkową 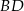 do boku
do boku 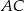 . Punkt
. Punkt 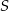 jest środkiem odcinka
jest środkiem odcinka 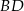 . Przez punkty
. Przez punkty 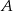 i
i 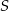 poprowadzono prostą, która przecięła bok
poprowadzono prostą, która przecięła bok 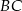 w punkcie
w punkcie 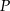 . Wykaż, że długość odcinka
. Wykaż, że długość odcinka 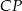 jest równa
jest równa 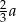 .
.
Dany jest trójkąt 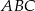 oraz punkt
oraz punkt 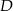 na jego boku
na jego boku 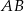 taki, że
taki, że 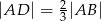 . Z wierzchołka
. Z wierzchołka 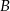 poprowadzono środkową
poprowadzono środkową 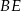 do boku
do boku 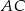 . Punkt
. Punkt 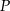 jest punktem wspólnym odcinków
jest punktem wspólnym odcinków 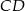 i
i 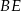 . Wykaż, że punkt
. Wykaż, że punkt 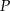 jest środkiem odcinka
jest środkiem odcinka 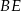 .
.
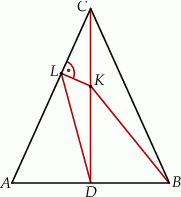
Odcinek 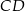 jest wysokością przedstawionego na rysunku trójkąta równoramiennego
jest wysokością przedstawionego na rysunku trójkąta równoramiennego 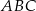 , w którym
, w którym 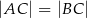 . Punkt
. Punkt 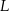 jest rzutem punktu
jest rzutem punktu 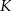 wysokości
wysokości 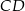 na bok
na bok 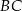 . Udowodnij, że
. Udowodnij, że 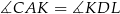 .
.
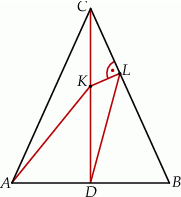
Odcinek 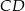 jest wysokością przedstawionego na rysunku trójkąta równoramiennego
jest wysokością przedstawionego na rysunku trójkąta równoramiennego 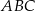 , w którym
, w którym 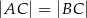 . Punkt
. Punkt 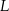 jest rzutem punktu
jest rzutem punktu 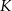 wysokości
wysokości 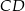 na bok
na bok 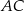 . Udowodnij, że trójkąt
. Udowodnij, że trójkąt 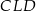 jest podobny do trójkąta
jest podobny do trójkąta 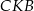 .
.
Wykaż, że w trójkącie prostokątnym suma długości obu przyprostokątnych jest równa sumie długości średnic okręgów wpisanego i opisanego na tym trójkącie.
Przyprostokątne trójkąta prostokątnego mają długości  i
i 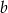 , a jego przeciwprostokątna ma długość
, a jego przeciwprostokątna ma długość  . Wykaż, że promień okręgu wpisanego w ten trójkąt ma długość
. Wykaż, że promień okręgu wpisanego w ten trójkąt ma długość 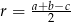 .
.
Wewnątrz kąta o mierze 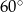 leży punkt
leży punkt 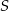 . Odległość tego punktu od ramion kąta wynosi odpowiednio
. Odległość tego punktu od ramion kąta wynosi odpowiednio 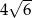 i
i 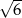 . Oblicz odległość tego punktu od wierzchołka kąta.
. Oblicz odległość tego punktu od wierzchołka kąta.
Punkt 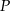 należy do okręgu opisanego na kwadracie
należy do okręgu opisanego na kwadracie 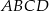 . Wykaż, że wyrażenie
. Wykaż, że wyrażenie 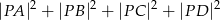 ma stałą wartość, niezależną od wyboru punktu
ma stałą wartość, niezależną od wyboru punktu 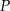 .
.
W trapezie 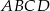 o podstawach
o podstawach 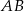 i
i 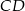 punkt
punkt 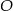 jest punktem wspólnym przekątnych. Oblicz pole trapezu wiedząc, że pole trójkąta
jest punktem wspólnym przekątnych. Oblicz pole trapezu wiedząc, że pole trójkąta 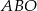 jest równe 5, a pole trójkąta
jest równe 5, a pole trójkąta 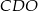 jest równe 4.
jest równe 4.
Oblicz jaka może być najmniejsza możliwa długość przeciwprostokątnej trójkąta prostokątnego o polu 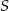 .
.
Z przeciwległych wierzchołków prostokąta poprowadzono odcinki prostopadłe do przekątnej. Odcinki te dzielą przekątną na trzy części. Każda z nich jest odcinkiem o długości 4 cm. Oblicz pole tego prostokąta.
Uzasadnij, że suma długości wysokości w dowolnym trójkącie jest mniejsza od jego obwodu.
Dany jest trapez 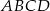 o podstawach
o podstawach 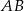 i
i 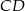 . Przekątne tego trapezu przecinają się w punkcie
. Przekątne tego trapezu przecinają się w punkcie 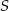 . Wykaż, że
. Wykaż, że 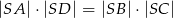 .
.
W trapezie 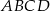 o podstawach
o podstawach 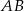 i
i 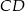 punkt
punkt 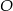 jest punktem wspólnym przekątnych. Oblicz pole trapezu wiedząc, że pole trójkąta
jest punktem wspólnym przekątnych. Oblicz pole trapezu wiedząc, że pole trójkąta 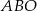 jest równe
jest równe 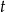 , a pole trójkąta
, a pole trójkąta 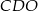 jest równe
jest równe  .
.
W trójkącie 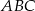 na boku
na boku 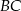 zaznaczono punkt
zaznaczono punkt 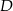 , na boku
, na boku 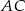 zaznaczono punkt
zaznaczono punkt 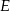 , na boku
, na boku 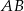 punkt
punkt 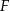 . Poprowadzono okręgi
. Poprowadzono okręgi 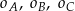 , w ten sposób, że do okręgu
, w ten sposób, że do okręgu 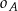 należą punkty
należą punkty 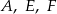 , do
, do 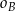 – punkty
– punkty 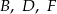 , a do
, a do 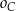 – punkty
– punkty 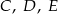 . Wykaż, że te trzy okręgi przecinają się w jednym punkcie.
. Wykaż, że te trzy okręgi przecinają się w jednym punkcie.
Okrąg 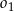 przechodzi przez wierzchołek
przechodzi przez wierzchołek 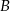 trójkąta
trójkąta 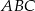 i przecina jego boki
i przecina jego boki 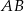 i
i 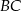 odpowiednio w punktach
odpowiednio w punktach 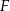 i
i 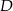 . Okrąg
. Okrąg 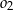 przechodzi przez wierzchołek
przechodzi przez wierzchołek 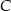 , przecina okrąg
, przecina okrąg 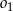 w punkcie
w punkcie 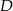 oraz w punkcie
oraz w punkcie 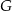 leżącym wewnątrz trójkąta
leżącym wewnątrz trójkąta 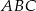 . Ponadto okrąg
. Ponadto okrąg 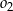 przecina bok
przecina bok 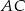 trójkąta w punkcie
trójkąta w punkcie 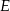 .
.
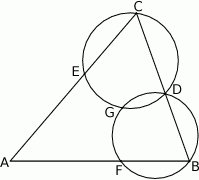
Udowodnij, że punkt 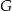 leży na okręgu opisanym na trójkącie
leży na okręgu opisanym na trójkącie 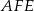 .
.
Oblicz pole trapezu, którego podstawy mają długości 2 i 3, a przekątne długości 3 i 4.
W trójkącie 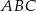 na boku
na boku 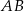 wybrano takie punkty
wybrano takie punkty 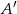 i
i 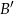 , że
, że
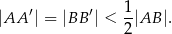
Przez punkty 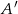 i
i 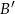 poprowadzono proste równoległe do boków odpowiednio
poprowadzono proste równoległe do boków odpowiednio 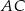 i
i 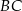 . Proste te przecięły się w punkcie
. Proste te przecięły się w punkcie 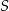 . Wykaż, że odcinek
. Wykaż, że odcinek 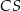 jest zawarty w środkowej trójkąta
jest zawarty w środkowej trójkąta 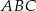 .
.

