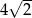Wykaż, że jeżeli przy dzieleniu przez 7 jedna liczba daję resztę 3, a druga resztę 4, to iloczyn tych liczb daje przy dzieleniu przez 7 resztę 5.
/Szkoła podstawowa
Udowodnij, że jeżeli przy dzieleniu przez 5 liczba całkowita  daje resztę 2, a liczba całkowita
daje resztę 2, a liczba całkowita 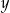 daje resztę 3, to iloczyn liczb
daje resztę 3, to iloczyn liczb  i
i 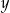 przy dzieleniu przez 5 daje resztę 1.
przy dzieleniu przez 5 daje resztę 1.
Liczba naturalna  przy dzieleniu przez 5 daje resztę 3, liczba
przy dzieleniu przez 5 daje resztę 3, liczba 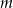 również przy dzieleniu przez 5 resztę 2. Udowodnij, że reszta z dzielenia iloczynu liczb
również przy dzieleniu przez 5 resztę 2. Udowodnij, że reszta z dzielenia iloczynu liczb 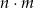 przez 5 daje resztę 1.
przez 5 daje resztę 1.
Wykaż, że jeżeli przy dzieleniu przez 5 jedna liczba daję resztę 2, a druga resztę 3, to iloczyn tych liczb daje przy dzieleniu przez 5 resztę 1.
Wśród uczniów klas ósmych przeprowadzono ankietę. Jedno z pytań tej ankiety zamieszczono poniżej.

Każdy z uczniów wypełniających ankietę zaznaczył tylko jedną odpowiedź. Czworo spośród ankietowanych zaznaczyło odpowiedź żadne z wymienionych. Procentowy rozkład udzielonych odpowiedzi uczniów przedstawiono na poniższym diagramie.
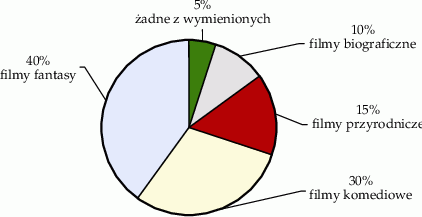
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| W ankiecie wzięło udział 80 uczniów. | P | F |
| Filmy fantasy wybrało o 20 uczniów więcej niż uczniów, którzy wybrali filmy przyrodnicze. | P | F |
Wśród uczniów klas ósmych przeprowadzono ankietę – uczniowie odpowiadali na pytanie „Jaki jest twój ulubiony sport?”. Każdy uczeń podawał tylko jedną dyscyplinę sportu. Grę w tenisa wskazało 24 uczniów. Procentowy rozkład udzielonych odpowiedzi uczniów przedstawiono na poniższym diagramie.
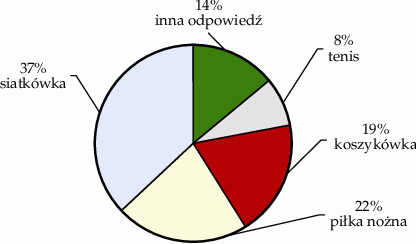
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Koszykówkę wybrało 57 uczniów. | P | F |
| Siatkówkę wybrało wybrało o 46 uczniów więcej niż uczniów, którzy wybrali piłkę nożną. | P | F |
Wśród uczniów klas siódmych przeprowadzono ankietę. Jedno z pytań tej ankiety zamieszczono poniżej.

Każdy z uczniów wypełniających ankietę zaznaczył tylko jedną odpowiedź. Odpowiedź filmy przyrodnicze otrzymała o 2 głosy więcej niż odpowiedź żadne z wymienionych. Procentowy rozkład wszystkich udzielonych odpowiedzi uczniów przedstawiono na poniższym diagramie.
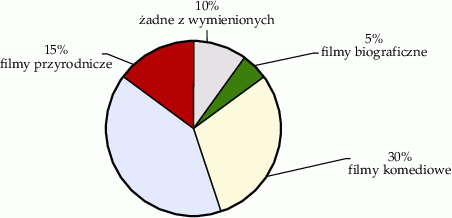
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Filmy komediowe wybrało 10 uczniów. | P | F |
| Liczba uczniów, którzy wybrali filmy fantasy była o 14 większa niż liczba uczniów, którzy wybrali filmy biograficzne. | P | F |
Oblicz obwód czworokąta o wierzchołkach: 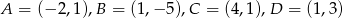 .
.
Która liczba jest większa: 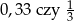 ?
?
Która liczba jest większa: 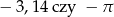 ?
?
Która liczba jest większa: 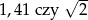 ?
?
Która liczba jest większa: 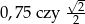 ?
?
Która liczba jest większa: 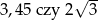 ?
?
Która liczba jest większa: 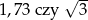 ?
?
Która liczba jest większa: 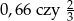 ?
?
Która liczba jest większa: 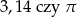 ?
?
Prostokątna ramka ma szerokość 2 cm oraz 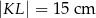 ,
, 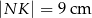 (patrz rysunek).
(patrz rysunek).
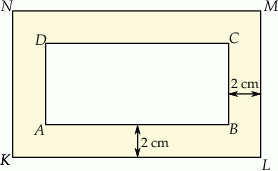
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Prostokąty 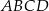 i i 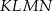 są podobne. są podobne. | P | F |
Obwód prostokąta 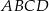 jest o 8 cm mniejszy od obwodu prostokąta jest o 8 cm mniejszy od obwodu prostokąta 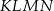 . . | P | F |
Zdanie: „Liczba  jest o 8 większa od potrojonego kwadratu liczby
jest o 8 większa od potrojonego kwadratu liczby  ” zapisane w postaci równania to
” zapisane w postaci równania to
A) 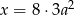 B)
B) 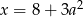 C)
C) 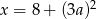 D)
D) 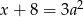
Zdanie: „Liczba  jest o 5 mniejsza od podwojonego kwadratu liczby
jest o 5 mniejsza od podwojonego kwadratu liczby 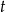 ” zapisane w postaci równania to
” zapisane w postaci równania to
A) 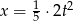 B)
B) 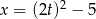 C)
C) 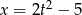 D)
D) 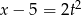
Zdanie: „Liczba  jest 3 razy większa od połowy sześcianu liczby
jest 3 razy większa od połowy sześcianu liczby 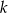 ” zapisane w postaci równania to
” zapisane w postaci równania to
A) 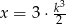 B)
B) 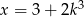 C)
C) 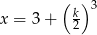 D)
D) 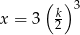
W sobotę Patrycja wyruszyła z Ptasiej Doliny na górski spacer, w trakcie którego odwiedziła kolejno dwa pobliskie szczyty: Kaczą Górę i Łąbędzią Górę. Na schematycznej mapce przedstawiono drogę jaką pokonała Patrycja, a na wykresie – jak zmieniała się w trakcie spaceru jej względna wysokość (w metrach) mierzona od poziomu Ptasiej Doliny.
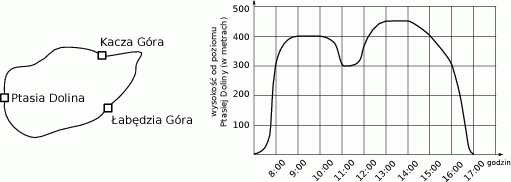
Jaka jest różnica wysokości między Łabędzią Górą, a Kaczą Górą?
A) 50 m B) 100 m C) 150 m D) 400 m
W sobotę Patrycja wyruszyła z Ptasiej Doliny na górski spacer, w trakcie którego odwiedziła kolejno dwa pobliskie szczyty: Kaczą Górę i Łąbędzią Górę. Na schematycznej mapce przedstawiono drogę jaką pokonała Patrycja, a na wykresie – jak zmieniała się w trakcie spaceru jej względna wysokość (w metrach) mierzona od poziomu Ptasiej Doliny.
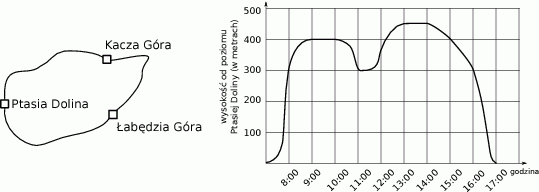
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Na każdym ze szczytów Patrycja zrobiła godzinną przerwę. | P | F |
| Od momentu zejścia z Kaczej Góry do momentu wejścia na Łąbędzią Górę upłynęły 4 godziny. | P | F |
| Patrycja wróciła do punktu wyjścia po 9 godzinach. | P | F |
| W ciągu przedostatniej godziny spaceru Patrycja zeszła w dół o 100 metrów. | P | F |
Suma wyrażeń 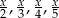 jest równa
jest równa
A) 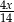 B)
B) 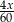 C)
C) 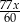 D)
D) 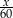
W pojemniku są wyłącznie kule białe, czerwone, niebieskie i żółte. Kul białych jest tyle samo co kul niebieskich, kul czerwonych jest dwa razy więcej niż kul żółtych, a stosunek liczby kul żółtych do liczby kul niebieskich jest równy 4 : 5. Z pojemnika losujemy jedną kulę. Prawdopodobieństwo wylosowania kuli, która nie jest czerwona jest równe
A) 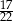 B)
B) 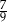 C)
C) 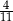 D)
D) 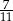
Zależność między liczbą przekątnych (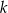 ) a liczbą boków (
) a liczbą boków ( ) wielokąta wypukłego określa wzór
) wielokąta wypukłego określa wzór 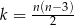 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Liczba przekątnych w dwunastokącie wypukłym jest trzy razy większa od liczby przekątnych w czworokącie wypukłym. | P | F |
| Liczba przekątnych w ośmiokącie wypukłym jest o 11 większa od liczby przekątnych w sześciokącie wypukłym. | P | F |
Zależność między liczbą przekątnych (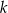 ) a liczbą boków (
) a liczbą boków ( ) wielokąta wypukłego określa wzór
) wielokąta wypukłego określa wzór 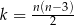 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Liczba przekątnych w dwunastokącie wypukłym jest sześć razy większa od liczby przekątnych w sześciokącie wypukłym. | P | F |
| Liczba przekątnych w siedmiokącie wypukłym jest o 10 większa od liczby przekątnych w czworokącie wypukłym. | P | F |
Suma pięciu kolejnych liczb całkowitych jest równa 195. Najmniejszą z tych liczb jest
A) 37 B) 38 C) 39 D) 40
Suma sześciu kolejnych liczb całkowitych jest równa 189. Najmniejszą z tych liczb jest
A) 32 B) 31 C) 30 D) 29
Obwód rombu wynosi 18 cm, a jego pole 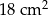 . Oblicz wysokość tego rombu.
. Oblicz wysokość tego rombu.
Ania otrzymała z pięciu sprawdzianów z matematyki następujące oceny: 5, 2, 3, 2, 5. Po kolejnych dwóch sprawdzianach średnia ocen Ani ze wszystkich sprawdzianów wyniosła 4. Jakie oceny mogła otrzymać Ania z ostatnich dwóch sprawdzianów?
A) 4 i 5 B) 5 i 5 C) 6 i 6 D) 5 i 6
Tomek otrzymał z sześciu sprawdzianów z matematyki następujące oceny: 5, 4, 2, 3, 2, 3. Po kolejnych dwóch sprawdzianach średnia ocen Tomka ze wszystkich sprawdzianów wyniosła 3,5. Jakie oceny mógł otrzymać Tomek z ostatnich dwóch sprawdzianów?
A) 4 i 4 B) 4 i 5 C) 3 i 4 D) 5 i 3
W pierwszej urnie znajduje się 5 kul białych i 17 kul czarnych. W drugiej urnie znajduje się 16 kul białych i 34 kule czarne. Ile kul białych należy przełożyć z drugiej urny do pierwszej, aby wylosowanie kuli białej z obu urn było jednakowo prawdopodobne?
W pierwszej urnie znajdują się 4 kule białe i 13 kul czarnych. W drugiej urnie znajduje się 17 kul białych i 26 kul czarnych. Ile kul białych należy przełożyć z drugiej urny do pierwszej, aby wylosowanie kuli białej z obu urn było jednakowo prawdopodobne?
Niech 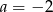 ,
, 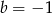 i
i 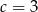 . Wartość wyrażenia
. Wartość wyrażenia 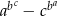 jest równa
jest równa
A) 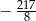 B)
B) 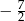 C)
C) 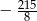 D)
D) 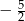
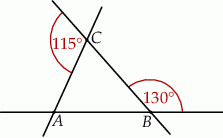
Trzy proste przecinające się w sposób przedstawiony na rysunku tworzą trójkąt 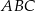 . Uzasadnij, że trójkąt
. Uzasadnij, że trójkąt 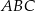 jest równoramienny.
jest równoramienny.
Na rysunku przedstawiono ostrosłup prawidłowy czworokątny i sześcian. Bryły mają jednakowe podstawy i równe wysokości, a suma objętości tych brył jest równa 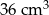 .
.
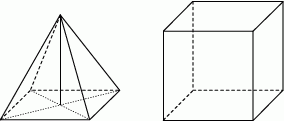
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Objętość sześcianu jest trzy razy większa od objętości ostrosłupa. | P | F |
| Krawędź sześcianu ma długość 3 cm. | P | F |
Na rysunku przedstawiono ostrosłup prawidłowy trójkątny oraz graniastosłup prawidłowy trójkątny. Bryły mają jednakowe podstawy i równe wysokości, a iloczyn objętości tych brył jest równy 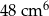 .
.
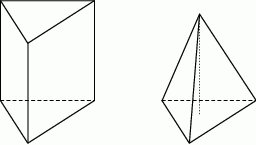
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Objętość ostrosłupa jest równa 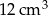 . . | P | F |
| Objętość graniastosłupa jest trzy razy większa od objętości ostrosłupa. | P | F |
Na rysunku przedstawiono sześcian i ostrosłup prawidłowy czworokątny. Bryły mają jednakowe podstawy i równe wysokości, a różnica objętości tych brył jest równa 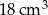 .
.
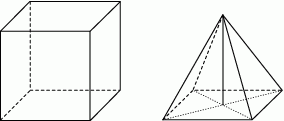
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Objętość ostrosłupa jest sześć razy mniejsza od objętości sześcianu. | P | F |
| Wysokość ostrosłupa ma długość 6 cm. | P | F |
Suma cyfr pewnej liczby dwucyfrowej wynosi 9. Jeśli między cyfrę dziesiątek a cyfrę jedności wstawimy zero, to otrzymamy liczbę o 90 większą. Jaka to liczba?
Piotrek ma 17 lat, a jego tata ma o 34 lata więcej. Wynika stąd, że tata ma od syna
A) 3 razy więcej lat B) 0 100% więcej lat C) 2 razy więcej lat D) o 50% więcej lat
Zenek ma 19 lat, a jego tata ma o 38 lat więcej. Wynika stąd, że tata ma od syna
A) o 300% więcej lat B) 0 100% więcej lat C) 2 razy więcej lat D) 3 razy więcej lat
Ewa ma 11 lat, a jej tata ma o 33 lata więcej. Wynika stąd, że tata ma od córki
A) 3 razy więcej lat B) 0 200% więcej lat C) 4 razy więcej lat D) o 100% więcej lat
Kwadrat jest wpisany w okrąg o średnicy 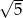 . Bok kwadratu jest równy
. Bok kwadratu jest równy
A) 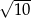 B)
B) 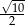 C)
C) 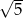 D)
D) 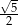
Okrąg opisany na kwadracie ma promień 8. Długość boku tego kwadratu jest równa
A) 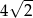 B)
B) 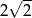 C)
C) 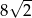 D) 8
D) 8
Kwadrat jest wpisany w okrąg o średnicy 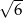 . Bok kwadratu jest równy
. Bok kwadratu jest równy
A) 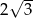 B)
B) 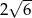 C)
C) 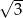 D) 3
D) 3
Okrąg opisany na kwadracie ma promień 6. Długość boku tego kwadratu jest równa
A) 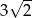 B)
B) 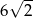 C) 12 D) 6
C) 12 D) 6
Okrąg opisany na kwadracie ma promień 4. Długość boku tego kwadratu jest równa
A) 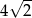 B)
B) 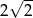 C) 8 D) 4
C) 8 D) 4
Kwadrat jest wpisany w okrąg o średnicy 4. Bok kwadratu jest równy
A) 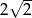 B)
B) 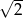 C)
C) 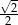 D)
D)