Podstawą ostrosłupa 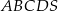 jest prostokąt
jest prostokąt 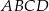 o bokach długości
o bokach długości  i
i 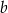 . Krawędź
. Krawędź 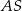 jest prostopadła do płaszczyzny podstawy. Odległość wierzchołka
jest prostopadła do płaszczyzny podstawy. Odległość wierzchołka 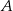 od krawędzi
od krawędzi 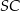 jest równa
jest równa 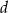 . Wyznacz objętość tego ostrosłupa.
. Wyznacz objętość tego ostrosłupa.
/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Dowolny
W czworościanie 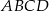 krawędź
krawędź 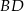 ma długość 2, a wszystkie pozostałe krawędzie mają długość 4.
ma długość 2, a wszystkie pozostałe krawędzie mają długość 4.
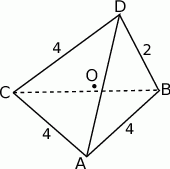
- Oblicz odległość krawędzi
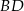 od krawędzi
od krawędzi 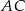 .
. - Wiedząc, że punkt
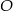 jest równoodległy od wszystkich wierzchołków czworościanu, oblicz długość odcinka
jest równoodległy od wszystkich wierzchołków czworościanu, oblicz długość odcinka 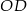 .
.
Podstawą ostrosłupa 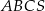 jest trójkąt równoboczny
jest trójkąt równoboczny 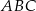 o boku długości 8. Punkt
o boku długości 8. Punkt 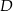 jest środkiem krawędzi
jest środkiem krawędzi 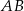 , odcinek
, odcinek 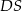 jest wysokością ostrosłupa. Krawędzie
jest wysokością ostrosłupa. Krawędzie 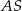 i
i 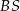 mają długość 7. Oblicz długość krawędzi
mają długość 7. Oblicz długość krawędzi 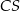 tego ostrosłupa.
tego ostrosłupa.
Podstawą ostrosłupa 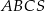 jest trójkąt równoboczny
jest trójkąt równoboczny 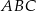 o boku długości 6. Punkt
o boku długości 6. Punkt 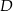 jest środkiem krawędzi
jest środkiem krawędzi 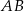 , odcinek
, odcinek 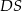 jest wysokością ostrosłupa. Krawędzie
jest wysokością ostrosłupa. Krawędzie 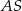 i
i 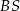 mają długość 8. Oblicz długość krawędzi
mają długość 8. Oblicz długość krawędzi 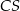 tego ostrosłupa.
tego ostrosłupa.
Podstawą ostrosłupa 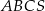 jest trójkąt równoboczny
jest trójkąt równoboczny 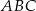 o boku długości 6. Punkt
o boku długości 6. Punkt 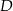 jest środkiem krawędzi
jest środkiem krawędzi 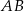 , odcinek
, odcinek 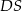 jest wysokością ostrosłupa. Krawędzie
jest wysokością ostrosłupa. Krawędzie 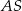 i
i 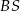 mają długość
mają długość 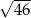 . Oblicz długość krawędzi
. Oblicz długość krawędzi 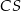 tego ostrosłupa.
tego ostrosłupa.
Podstawą ostrosłupa 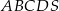 jest czworokąt wypukły
jest czworokąt wypukły 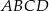 , w którym
, w którym 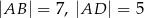 oraz
oraz 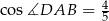 . Każda z krawędzi bocznych ostrosłupa ma długość
. Każda z krawędzi bocznych ostrosłupa ma długość 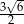 . Oblicz wysokość ostrosłupa.
. Oblicz wysokość ostrosłupa.
Podstawą ostrosłupa 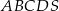 jest czworokąt wypukły
jest czworokąt wypukły 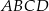 , w którym
, w którym 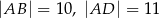 oraz
oraz 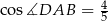 . Każda z krawędzi bocznych ostrosłupa ma długość 6. Oblicz wysokość ostrosłupa.
. Każda z krawędzi bocznych ostrosłupa ma długość 6. Oblicz wysokość ostrosłupa.
Podstawą ostrosłupa 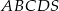 jest romb
jest romb 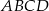 o boku długości 4. Kąt
o boku długości 4. Kąt 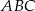 rombu ma miarę
rombu ma miarę 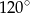 oraz
oraz 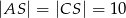 i
i 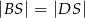 . Oblicz sinus kąta nachylenia krawędzi
. Oblicz sinus kąta nachylenia krawędzi 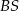 do płaszczyzny podstawy ostrosłupa.
do płaszczyzny podstawy ostrosłupa.
Podstawą ostrosłupa prawidłowego czworokątnego 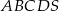 jest kwadrat
jest kwadrat 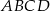 . Pole trójkąta równoramiennego
. Pole trójkąta równoramiennego 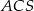 jest równe 120 oraz
jest równe 120 oraz 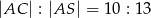 . Oblicz pole powierzchni bocznej tego ostrosłupa.
. Oblicz pole powierzchni bocznej tego ostrosłupa.
W ostrosłupie 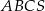 podstawa
podstawa 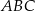 jest trójkątem równobocznym o boku długości
jest trójkątem równobocznym o boku długości  . Krawędź
. Krawędź 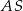 jest prostopadła do płaszczyzny podstawy. Odległość wierzchołka
jest prostopadła do płaszczyzny podstawy. Odległość wierzchołka 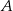 od ściany
od ściany 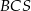 jest równa
jest równa 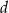 . Wyznacz objętość tego ostrosłupa.
. Wyznacz objętość tego ostrosłupa.
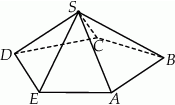
Dany jest ostrosłup o podstawie pięciokątnej 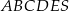 (zobacz rysunek). Każda ze ścian bocznych tego ostrosłupa jest trójkątem o polu trzy razy mniejszym niż pole pięciokąta
(zobacz rysunek). Każda ze ścian bocznych tego ostrosłupa jest trójkątem o polu trzy razy mniejszym niż pole pięciokąta 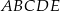 . Pole powierzchni całkowitej tego ostrosłupa jest równe 136. Oblicz pole jego podstawy.
. Pole powierzchni całkowitej tego ostrosłupa jest równe 136. Oblicz pole jego podstawy.
Podstawą ostrosłupa jest romb o boku długości 18 cm. Każda ze ścian bocznych tworzy z płaszczyzną podstawy kąt 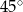 . Pole powierzchni bocznej ostrosłupa jest równe
. Pole powierzchni bocznej ostrosłupa jest równe 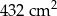 . Oblicz jego objętość.
. Oblicz jego objętość.
Oblicz objętość ostrosłupa trójkątnego 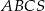 , którego siatkę przedstawiono na rysunku.
, którego siatkę przedstawiono na rysunku.
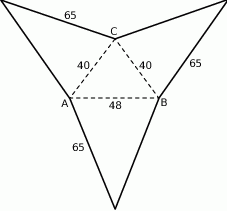
Podstawą ostrosłupa jest trójkąt o danych kątach  i
i 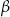 . Wszystkie krawędzie boczne mają długość
. Wszystkie krawędzie boczne mają długość 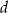 i są nachylone do płaszczyzny podstawy pod kątem o mierze
i są nachylone do płaszczyzny podstawy pod kątem o mierze 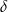 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Podstawą ostrosłupa 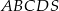 jest romb o boku długości 6. Krawędź boczna
jest romb o boku długości 6. Krawędź boczna 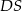 ma długość 8 i jest jednocześnie wysokością tego ostrosłupa. Długości pozostałych trzech krawędzi bocznych są równe (zobacz rysunek).
ma długość 8 i jest jednocześnie wysokością tego ostrosłupa. Długości pozostałych trzech krawędzi bocznych są równe (zobacz rysunek).
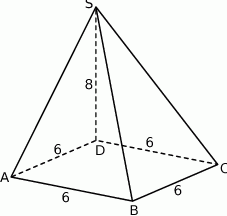
Oblicz objętość tego ostrosłupa.
Podstawą ostrosłupa 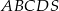 jest prostokąt
jest prostokąt 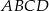 , a krawędź boczna
, a krawędź boczna 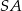 jest jego wysokością. Wykaż, że suma kwadratów pól ścian
jest jego wysokością. Wykaż, że suma kwadratów pól ścian 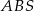 i
i 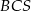 jest równa sumie kwadratów pól ścian
jest równa sumie kwadratów pól ścian 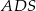 i
i 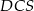 .
.
Trójkąt 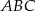 jest podstawą ostrosłupa
jest podstawą ostrosłupa 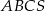 . Punkt
. Punkt 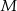 jest środkiem boku
jest środkiem boku 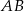 i
i 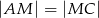 . Odcinek
. Odcinek 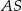 jest wysokością tego ostrosłupa. Wykaż, że kąt
jest wysokością tego ostrosłupa. Wykaż, że kąt 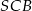 jest prosty.
jest prosty.
Podstawą ostrosłupa 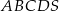 jest prostokąt, którego boki pozostają w stosunku 3:4, a pole jest równe 192 (zobacz rysunek). Punkt
jest prostokąt, którego boki pozostają w stosunku 3:4, a pole jest równe 192 (zobacz rysunek). Punkt 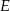 jest wyznaczony przez przecinające się przekątne podstawy, a odcinek
jest wyznaczony przez przecinające się przekątne podstawy, a odcinek 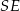 jest wysokością ostrosłupa. Każda krawędź boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem
jest wysokością ostrosłupa. Każda krawędź boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem 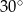 . Oblicz objętość ostrosłupa.
. Oblicz objętość ostrosłupa.
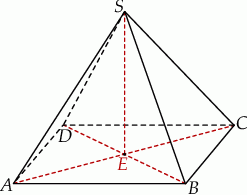
Podstawą ostrosłupa 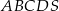 jest prostokąt o polu równym 432, a stosunek długości boków tego prostokąta jest równy 3:4. Przekątne podstawy
jest prostokąt o polu równym 432, a stosunek długości boków tego prostokąta jest równy 3:4. Przekątne podstawy 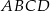 przecinają się w punkcie
przecinają się w punkcie 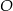 . Odcinek
. Odcinek 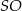 jest wysokością ostrosłupa (zobacz rysunek). Kąt
jest wysokością ostrosłupa (zobacz rysunek). Kąt 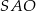 ma miarę
ma miarę 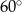 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
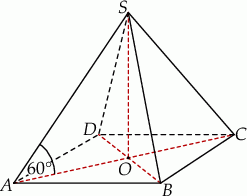
Podstawą ostrosłupa 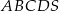 jest prostokąt, którego boki pozostają w stosunku 5:12, a pole jest równe 240 (zobacz rysunek). Punkt
jest prostokąt, którego boki pozostają w stosunku 5:12, a pole jest równe 240 (zobacz rysunek). Punkt 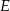 jest wyznaczony przez przecinające się przekątne podstawy, a odcinek
jest wyznaczony przez przecinające się przekątne podstawy, a odcinek 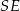 jest wysokością ostrosłupa. Każda krawędź boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem
jest wysokością ostrosłupa. Każda krawędź boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem 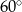 . Oblicz objętość ostrosłupa.
. Oblicz objętość ostrosłupa.
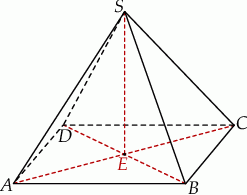
Podstawą ostrosłupa 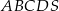 jest prostokąt
jest prostokąt 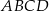 , którego boki mają długości
, którego boki mają długości 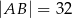 i
i 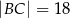 . Ściany boczne
. Ściany boczne 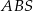 i
i 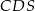 są trójkątami przystającymi i każda z nich jest nachylona do płaszczyzny podstawy ostrosłupa pod kątem
są trójkątami przystającymi i każda z nich jest nachylona do płaszczyzny podstawy ostrosłupa pod kątem  . Ściany boczne
. Ściany boczne 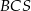 i
i 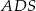 są trójkątami przystającymi i każda z nich jest nachylona do płaszczyzny podstawy pod kątem
są trójkątami przystającymi i każda z nich jest nachylona do płaszczyzny podstawy pod kątem 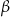 . Miary kątów
. Miary kątów  i
i 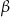 spełniają warunek:
spełniają warunek: 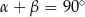 . Oblicz
. Oblicz 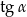 oraz pole powierzchni całkowitej tego ostrosłupa.
oraz pole powierzchni całkowitej tego ostrosłupa.
W graniastosłupie prawidłowym czworokątnym 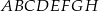 przekątna
przekątna 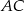 podstawy ma długość 4. Kąt
podstawy ma długość 4. Kąt 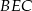 jest równy
jest równy 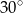 . Oblicz objętość ostrosłupa
. Oblicz objętość ostrosłupa 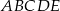 przedstawionego na poniższym rysunku.
przedstawionego na poniższym rysunku.
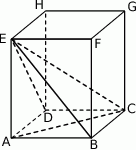
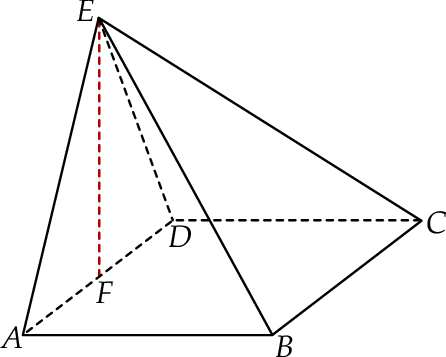
Podstawą ostrosłupa 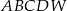 jest prostokąt
jest prostokąt 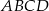 . Krawędź boczna
. Krawędź boczna 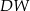 jest wysokością tego ostrosłupa. Krawędzie boczne
jest wysokością tego ostrosłupa. Krawędzie boczne 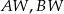 i
i 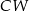 mają następujące długości:
mają następujące długości: 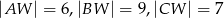 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
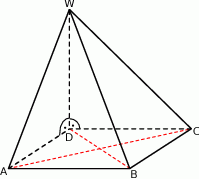
Podstawą ostrosłupa 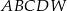 jest kwadrat
jest kwadrat 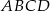 . Krawędź boczna
. Krawędź boczna 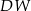 jest wysokością tego ostrosłupa. Krawędzie boczne
jest wysokością tego ostrosłupa. Krawędzie boczne 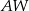 i
i 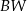 mają następujące długości:
mają następujące długości: 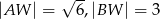 . Oblicz pole powierzchni całkowitej tego ostrosłupa.
. Oblicz pole powierzchni całkowitej tego ostrosłupa.
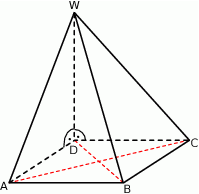
Podstawą ostrosłupa 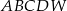 jest kwadrat
jest kwadrat 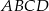 o polu 2. Krawędź boczna
o polu 2. Krawędź boczna 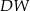 jest wysokością tego ostrosłupa. Długości krawędzi bocznych
jest wysokością tego ostrosłupa. Długości krawędzi bocznych 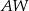 i
i 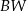 spełniają warunek
spełniają warunek 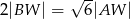 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
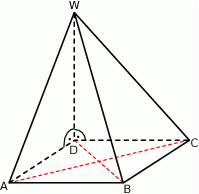
W ostrosłupie trójkątnym wszystkie krawędzie boczne i dwie krawędzie podstawy mają długość 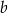 , a kąt między równymi bokami podstawy ma miarę
, a kąt między równymi bokami podstawy ma miarę  . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Podstawą ostrosłupa 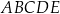 jest kwadrat o boku długości 12. Spodek
jest kwadrat o boku długości 12. Spodek 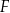 wysokości
wysokości 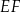 ostrosłupa jest środkiem krawędzi
ostrosłupa jest środkiem krawędzi 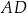 . Wiedząc, że dwie krótsze krawędzie boczne mają tę samą długość, równą 10, oblicz tangens kąta nachylenia krawędzi
. Wiedząc, że dwie krótsze krawędzie boczne mają tę samą długość, równą 10, oblicz tangens kąta nachylenia krawędzi 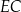 do płaszczyzny podstawy.
do płaszczyzny podstawy.