Podstawą ostrosłupa jest równoramienny trójkąt prostokątny. Każda krawędź boczna ma długość 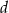 i jest nachylona do płaszczyzny podstawy pod kątem
i jest nachylona do płaszczyzny podstawy pod kątem  . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Dowolny
Podstawą ostrosłupa 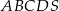 jest prostokąt
jest prostokąt 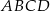 , w którym
, w którym 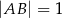 ,
, 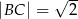 . Wszystkie krawędzie boczne tego ostrosłupa mają długość 1. Wyznacz cosinus kąta między dwiema sąsiednimi ścianami bocznymi tego ostrosłupa.
. Wszystkie krawędzie boczne tego ostrosłupa mają długość 1. Wyznacz cosinus kąta między dwiema sąsiednimi ścianami bocznymi tego ostrosłupa.
Podstawą ostrosłupa  jest trójkąt równoramienny
jest trójkąt równoramienny 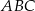 , w którym
, w którym 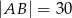 ,
, 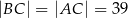 . Spodek wysokości ostrosłupa należy do jego podstawy, a każda wysokość ściany bocznej poprowadzona z wierzchołka
. Spodek wysokości ostrosłupa należy do jego podstawy, a każda wysokość ściany bocznej poprowadzona z wierzchołka 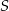 ma długość 26. Oblicz objętość tego ostrosłupa.
ma długość 26. Oblicz objętość tego ostrosłupa.
Podstawą ostrosłupa 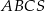 jest trójkąt równoramienny
jest trójkąt równoramienny 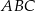 , w którym
, w którym 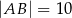 ,
, 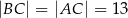 i spodek wysokości ostrosłupa należy do jego podstawy. Każda wysokość ściany bocznej poprowadzona z wierzchołka
i spodek wysokości ostrosłupa należy do jego podstawy. Każda wysokość ściany bocznej poprowadzona z wierzchołka 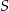 ma długość
ma długość 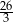 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Podstawą ostrosłupa jest romb, którego pole wynosi 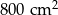 , a kąt ostry rombu ma miarę
, a kąt ostry rombu ma miarę 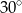 . Wysokość ostrosłupa jest równa 24 cm, a spodek tej wysokości jest środkiem okręgu wpisanego w podstawę. Oblicz:
. Wysokość ostrosłupa jest równa 24 cm, a spodek tej wysokości jest środkiem okręgu wpisanego w podstawę. Oblicz:
- promień tego okręgu,
- pole powierzchni bocznej ostrosłupa.
Podstawą ostrosłupa 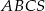 jest trójkąt równoramienny
jest trójkąt równoramienny 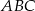 , w którym
, w którym 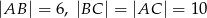 , a wszystkie krawędzie boczne tworzą z płaszczyzną podstawy kąt
, a wszystkie krawędzie boczne tworzą z płaszczyzną podstawy kąt 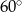 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Podstawą ostrosłupa 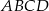 jest trójkąt
jest trójkąt 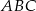 , a krawędź
, a krawędź 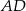 jest wysokością ostrosłupa. Oblicz pole powierzchni całkowitej ostrosłupa
jest wysokością ostrosłupa. Oblicz pole powierzchni całkowitej ostrosłupa 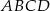 , jeśli wiadomo, że jego objętość jest równa 48 oraz
, jeśli wiadomo, że jego objętość jest równa 48 oraz 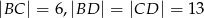 . Podaj wszystkie możliwe odpowiedzi.
. Podaj wszystkie możliwe odpowiedzi.
Podstawą ostrosłupa 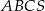 jest trójkąt równoramienny
jest trójkąt równoramienny 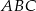 . Krawędź
. Krawędź 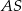 jest wysokością ostrosłupa oraz
jest wysokością ostrosłupa oraz 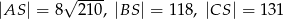 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
W ostrosłupie, którego podstawą jest trójkąt równoboczny o boku  , jedna z krawędzi bocznych jest prostopadła do podstawy. Dwie pozostałe krawędzie tworzą z podstawą kąty o mierze
, jedna z krawędzi bocznych jest prostopadła do podstawy. Dwie pozostałe krawędzie tworzą z podstawą kąty o mierze  . Znajdź pole największej ściany bocznej oraz tangens kąta nachylenia tej ściany do płaszczyzny podstawy.
. Znajdź pole największej ściany bocznej oraz tangens kąta nachylenia tej ściany do płaszczyzny podstawy.
Podstawą ostrosłupa 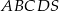 jest czworokąt
jest czworokąt 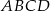 . Przekątna
. Przekątna 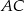 tego czworokąta ma długość
tego czworokąta ma długość 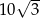 , a kąt
, a kąt 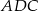 ma miarę
ma miarę 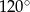 . Każda krawędź boczna tego ostrosłupa ma tę samą długość 26. Oblicz odległość środka wysokości tego ostrosłupa od krawędzi
. Każda krawędź boczna tego ostrosłupa ma tę samą długość 26. Oblicz odległość środka wysokości tego ostrosłupa od krawędzi 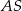 .
.
Podstawą ostrosłupa 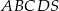 jest czworokąt
jest czworokąt 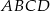 . Przekątna
. Przekątna 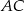 tego czworokąta ma długość
tego czworokąta ma długość 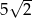 , a kąt
, a kąt 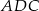 ma miarę
ma miarę 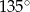 . Każda krawędź boczna tego ostrosłupa ma tę samą długość 13. Oblicz sumę odległości spodka wysokości ostrosłupa od krawędzi bocznych
. Każda krawędź boczna tego ostrosłupa ma tę samą długość 13. Oblicz sumę odległości spodka wysokości ostrosłupa od krawędzi bocznych 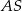 ,
, 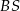 ,
, 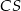 i
i 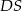 .
.
Podstawą ostrosłupa jest trójkąt równoramienny o ramieniu długości 10 i podstawie długości 12. Wszystkie krawędzie boczne ostrosłupa mają długość 7. Oblicz objętość i pole powierzchni bocznej tego ostrosłupa.
Podstawą ostrosłupa o objętości 30 jest trójkąt równoramienny o ramieniu długości 5 i podstawie długości 6. Oblicz pole powierzchni bocznej ostrosłupa wiedząc, że wszystkie krawędzie boczne mają jednakową długość.
Podstawą ostrosłupa 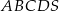 jest równoległobok
jest równoległobok 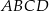 o przekątnej długości
o przekątnej długości 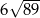 i bokach długości 32 i 34. Pole powierzchni bocznej jednej ze ścian bocznych ostrosłupa jest mniejsze od pola powierzchni sąsiedniej ściany bocznej i jest równe 1808. Spodek wysokości ostrosłupa pokrywa się z punktem przecięcia przekątnych równoległoboku
i bokach długości 32 i 34. Pole powierzchni bocznej jednej ze ścian bocznych ostrosłupa jest mniejsze od pola powierzchni sąsiedniej ściany bocznej i jest równe 1808. Spodek wysokości ostrosłupa pokrywa się z punktem przecięcia przekątnych równoległoboku 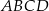 , a jego ściany boczne są trójkątami ostrokątnymi. Oblicz długość krótszej z krawędzi bocznych ostrosłupa
, a jego ściany boczne są trójkątami ostrokątnymi. Oblicz długość krótszej z krawędzi bocznych ostrosłupa 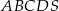 .
.
Dany jest ostrosłup, którego podstawą jest trójkąt równoboczny o boku 6. Jedna z krawędzi bocznych tego ostrosłupa ma długość 8 i jest prostopadła do płaszczyzny podstawy. Oblicz objętość tego ostrosłupa.
Podstawą ostrosłupa 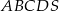 jest romb
jest romb 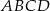 . Krawędź
. Krawędź 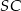 jest prostopadła do płaszczyzny podstawy, krawędź
jest prostopadła do płaszczyzny podstawy, krawędź 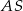 ma długość 4 i jest nachylona do płaszczyzny podstawy pod kątem
ma długość 4 i jest nachylona do płaszczyzny podstawy pod kątem 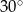 . Krawędź
. Krawędź 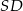 ma długość
ma długość 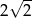 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Podstawą ostrosłupa jest prostokąt o polu 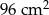 kwadratowych. Stosunek długości boków tego prostokąta wynosi 2:3. Krawędzie boczne ostrosłupa są nachylone do płaszczyzny podstawy pod kątem
kwadratowych. Stosunek długości boków tego prostokąta wynosi 2:3. Krawędzie boczne ostrosłupa są nachylone do płaszczyzny podstawy pod kątem 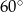 . Oblicz pole powierzchni całkowitej tej bryły.
. Oblicz pole powierzchni całkowitej tej bryły.
Podstawą ostrosłupa 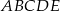 jest kwadrat
jest kwadrat 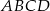 . Punkt
. Punkt 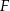 jest środkiem krawędzi
jest środkiem krawędzi 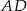 , odcinek
, odcinek 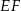 jest wysokością ostrosłupa. Oblicz objętość ostrosłupa, jeśli wiadomo, że
jest wysokością ostrosłupa. Oblicz objętość ostrosłupa, jeśli wiadomo, że 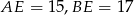 .
.
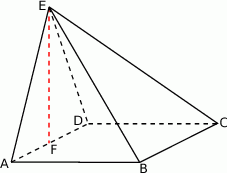
Podstawą ostrosłupa  jest trapez
jest trapez  . Przekątna
. Przekątna 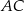 tego trapezu ma długość
tego trapezu ma długość 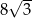 , jest prostopadła do ramienia
, jest prostopadła do ramienia 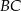 i tworzy z dłuższą podstawą
i tworzy z dłuższą podstawą 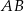 tego trapezu kąt o mierze
tego trapezu kąt o mierze 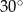 . Każda krawędź boczna tego ostrosłupa ma tę samą długość
. Każda krawędź boczna tego ostrosłupa ma tę samą długość 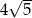 . Oblicz odległość spodka wysokości tego ostrosłupa od jego krawędzi bocznej
. Oblicz odległość spodka wysokości tego ostrosłupa od jego krawędzi bocznej 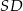 .
.
Podstawą ostrosłupa 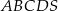 jest trapez
jest trapez 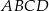 . Przekątna
. Przekątna 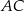 tego trapezu ma długość
tego trapezu ma długość 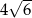 , jest prostopadła do ramienia
, jest prostopadła do ramienia 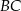 i tworzy z dłuższą podstawą
i tworzy z dłuższą podstawą 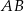 tego trapezu kąt o mierze
tego trapezu kąt o mierze 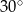 . Każda krawędź boczna tego ostrosłupa ma tę samą długość 9. Oblicz odległość spodka wysokości tego ostrosłupa od jego krawędzi bocznej
. Każda krawędź boczna tego ostrosłupa ma tę samą długość 9. Oblicz odległość spodka wysokości tego ostrosłupa od jego krawędzi bocznej 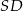 .
.
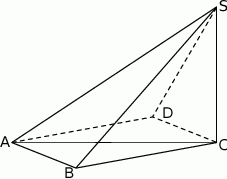
Podstawą ostrosłupa 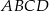 jest trójkąt
jest trójkąt 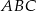 . Krawędź
. Krawędź 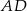 jest wysokością ostrosłupa (zobacz rysunek).
jest wysokością ostrosłupa (zobacz rysunek).
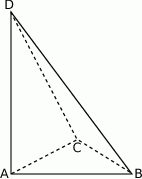
Oblicz objętość ostrosłupa 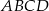 , jeśli wiadomo, że
, jeśli wiadomo, że 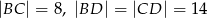 oraz pole podstawy jest równe 24.
oraz pole podstawy jest równe 24.
Podstawą ostrosłupa jest trójkąt, którego jeden bok ma długość 4, a kąty przyległe do tego boku mają miary 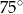 i
i 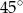 . Wysokość ostrosłupa ma długość równą długości promienia koła opisanego na podstawie. Oblicz objętość ostrosłupa. Wynik podaj w postaci
. Wysokość ostrosłupa ma długość równą długości promienia koła opisanego na podstawie. Oblicz objętość ostrosłupa. Wynik podaj w postaci 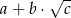 , gdzie
, gdzie  ,
, 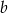 ,
,  są liczbami wymiernymi.
są liczbami wymiernymi.
Podstawą ostrosłupa jest trójkąt, którego jeden z boków ma długość 6, a kąty przyległe do niego mają miary 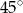 i
i 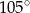 . Wysokość ostrosłupa ma długość równą długości promienia okręgu opisanego na podstawie. Oblicz objętość ostrosłupa. Wynik podaj w postaci
. Wysokość ostrosłupa ma długość równą długości promienia okręgu opisanego na podstawie. Oblicz objętość ostrosłupa. Wynik podaj w postaci 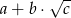 , gdzie
, gdzie  ,
, 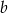 ,
,  są liczbami wymiernymi.
są liczbami wymiernymi.
Ostrosłup 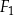 jest podobny do ostrosłupa
jest podobny do ostrosłupa 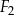 . Objętość ostrosłupa
. Objętość ostrosłupa 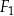 jest równa 64, a objętość ostrosłupa
jest równa 64, a objętość ostrosłupa 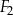 jest równa 512. Oblicz stosunek pola powierzchni całkowitej ostrosłupa
jest równa 512. Oblicz stosunek pola powierzchni całkowitej ostrosłupa 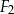 do pola powierzchni całkowitej ostrosłupa
do pola powierzchni całkowitej ostrosłupa 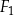 .
.
Podstawą ostrosłupa 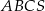 jest trójkąt
jest trójkąt  , w którym
, w którym 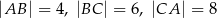 . Wszystkie ściany boczne tworzą z płaszczyzną podstawy kąt
. Wszystkie ściany boczne tworzą z płaszczyzną podstawy kąt 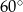 . Oblicz objętość ostrosłupa.
. Oblicz objętość ostrosłupa.

