Wysokość 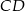 trójkąta
trójkąta 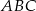 ma długość 6cm i dzieli bok
ma długość 6cm i dzieli bok 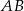 na odcinki o długościach
na odcinki o długościach 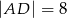 i
i 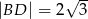 .
.
- Oblicz tangens i cosinus kąta
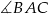 .
. - Znajdź miarę kąta
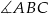 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wysokość 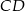 trójkąta
trójkąta 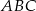 ma długość 6cm i dzieli bok
ma długość 6cm i dzieli bok 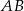 na odcinki o długościach
na odcinki o długościach 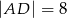 i
i 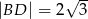 .
.
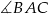 .
. 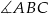 .
.Dwusieczne kątów 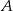 i
i 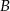 trójkąta
trójkąta 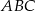 przecinają okrąg opisany na nim odpowiednio w punktach
przecinają okrąg opisany na nim odpowiednio w punktach 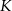 i
i 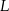 . Oblicz miary kątów czworokąta
. Oblicz miary kątów czworokąta 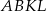 wiedząc, że
wiedząc, że 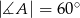 i
i 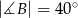 .
.
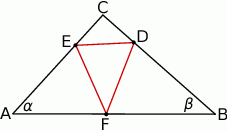
Dany jest trójkąt 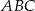 , w którym
, w którym 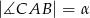 i
i 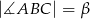 (zobacz rysunek). Na bokach
(zobacz rysunek). Na bokach 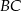 ,
, 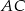 i
i 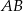 tego trójkąta wybrano odpowiednio punkty
tego trójkąta wybrano odpowiednio punkty 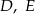 i
i 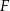 w taki sposób, że
w taki sposób, że 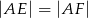 ,
, 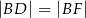 i
i 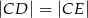 . Oblicz miary kątów trójkąta
. Oblicz miary kątów trójkąta 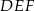 .
.
W okrąg wpisano trójkąt 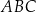 , w którym
, w którym 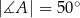 i
i 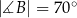 . Przez wierzchołek kąta
. Przez wierzchołek kąta 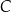 poprowadzono styczną do okręgu, przecinającą przedłużenie boku
poprowadzono styczną do okręgu, przecinającą przedłużenie boku 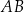 w punkcie
w punkcie 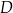 . Oblicz miary kątów trójkąta
. Oblicz miary kątów trójkąta 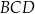 .
.
Wysokość 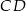 trójkąta
trójkąta 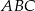 tworzy z bokami
tworzy z bokami 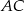 i
i 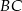 kąty o miarach równych odpowiednio
kąty o miarach równych odpowiednio 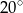 i
i 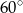 . Punkt
. Punkt 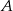 należy do odcinka
należy do odcinka 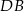 .
.
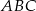 i jego wysokość
i jego wysokość 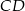 .
. 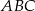 .
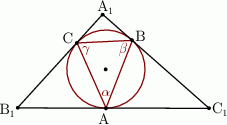
.Boki trójkąta 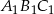 są styczne do okręgu w punktach
są styczne do okręgu w punktach 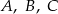 , a kąty trójkąta
, a kąty trójkąta 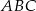 są odpowiednio równe
są odpowiednio równe 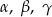 . Oblicz miary kątów trójkąta
. Oblicz miary kątów trójkąta 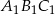 .
.
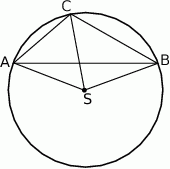
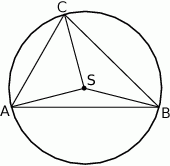
Punkt 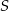 jest środkiem okręgu opisanego na trójkącie ostrokątnym
jest środkiem okręgu opisanego na trójkącie ostrokątnym 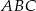 . Kąt
. Kąt 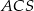 jest trzy razy większy od kąta
jest trzy razy większy od kąta 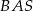 , a kąt
, a kąt 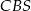 jest dwa razy większy od kąta
jest dwa razy większy od kąta 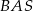 . Oblicz kąty trójkąta
. Oblicz kąty trójkąta 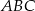 .
.
Punkt 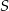 jest środkiem okręgu opisanego na trójkącie rozwartokątnym
jest środkiem okręgu opisanego na trójkącie rozwartokątnym 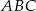 . Kąt
. Kąt 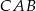 jest dwa razy większy od kąta
jest dwa razy większy od kąta 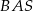 , a kąt
, a kąt 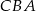 jest o
jest o 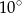 większy od kąta
większy od kąta 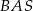 . Oblicz kąty trójkąta
. Oblicz kąty trójkąta 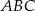 .
.