Oblicz cosinus najmniejszego kąta  trójkąta o bokach 2 cm, 4 cm, 5 cm.
trójkąta o bokach 2 cm, 4 cm, 5 cm.
/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny/Kąty
Dany jest trójkąt 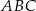 o bokach długości 6, 7 oraz 8. Oblicz cosinus największego kąta tego trójkąta.
o bokach długości 6, 7 oraz 8. Oblicz cosinus największego kąta tego trójkąta.
Dany jest trójkąt 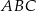 o bokach długości 6, 7 oraz 8. Oblicz cosinus najmniejszego kąta tego trójkąta.
o bokach długości 6, 7 oraz 8. Oblicz cosinus najmniejszego kąta tego trójkąta.
W trójkącie 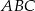 środkowa
środkowa 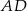 jest prostopadła do boku
jest prostopadła do boku 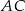 oraz
oraz 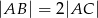 . Oblicz miarę kąta
. Oblicz miarę kąta 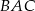 .
.
W trójkącie 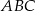 , w którym
, w którym 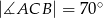 połączono środek okręgu wpisanego
połączono środek okręgu wpisanego 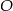 z wierzchołkami
z wierzchołkami 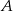 i
i 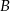 . Oblicz miarę kąta
. Oblicz miarę kąta 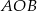 .
.
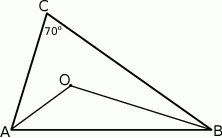
W trójkącie 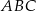 długość boku
długość boku 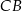 stanowi
stanowi 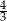 długości boku
długości boku 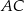 , a kąt
, a kąt 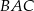 ma miarę
ma miarę 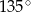 . Oblicz cosinus kąta
. Oblicz cosinus kąta 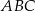 .
.
Środkowa 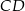 trójkąta
trójkąta 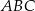 jest równa bokowi
jest równa bokowi 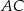 . Wyznacz kąty trójkąta
. Wyznacz kąty trójkąta 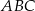 wiedząc, że
wiedząc, że 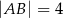 i
i 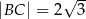 .
.
Środkowa 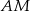 trójkąta
trójkąta 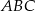 ma długość równą połowie długości boku
ma długość równą połowie długości boku 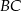 . Miara kąta między tą środkową a wysokością
. Miara kąta między tą środkową a wysokością 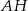 jest równa
jest równa 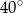 . Wyznacz miary kątów trójkąta
. Wyznacz miary kątów trójkąta 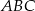 .
.
W okrąg wpisany jest trójkąt 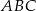 , przy czym
, przy czym 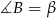 i
i 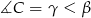 . Oblicz miarę kąta między prostą
. Oblicz miarę kąta między prostą 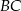 i styczną do okręgu w punkcie
i styczną do okręgu w punkcie 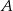 .
.
Wierzchołki 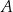 i
i 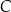 trójkąta
trójkąta 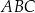 leżą na okręgu o promieniu
leżą na okręgu o promieniu  . Środek
. Środek 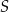 tego okręgu leży na boku
tego okręgu leży na boku 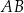 tego trójkąta (zobacz rysunek poniżej). Długości boków
tego trójkąta (zobacz rysunek poniżej). Długości boków 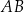 i
i 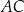 są równe odpowiednio
są równe odpowiednio 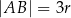 oraz
oraz 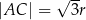 .
.
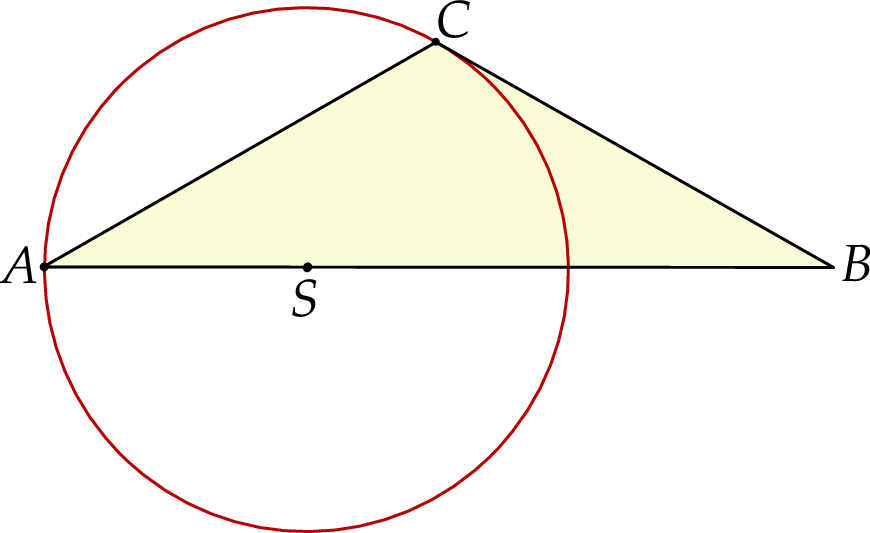
Oblicz miary wszystkich kątów wewnętrznych trójkąta 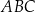 .
.
Długości boków trójkąta są w stosunku 2 : 3 : 4. Oblicz cosinus największego kąta tego trójkąta.
W trójkącie 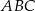 bok
bok 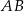 jest 3 razy dłuższy od boku
jest 3 razy dłuższy od boku 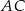 , a długość boku
, a długość boku 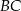 stanowi
stanowi  długości boku
długości boku 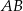 . Oblicz cosinus najmniejszego kąta trójkąta
. Oblicz cosinus najmniejszego kąta trójkąta 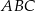 .
.
W trójkącie 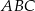 bok
bok 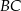 jest 3 razy krótszy od boku
jest 3 razy krótszy od boku 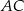 , a długość boku
, a długość boku 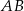 stanowi
stanowi  długości boku
długości boku 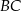 . Oblicz cosinus największego kąta trójkąta
. Oblicz cosinus największego kąta trójkąta 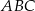 .
.
Dany jest trójkąt 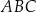 o bokach długości:
o bokach długości: 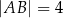 ,
, 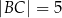 ,
, 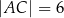 . Oblicz sinus najmniejszego kąta wewnętrznego trójkąta
. Oblicz sinus najmniejszego kąta wewnętrznego trójkąta 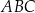 .
.
Miary dwóch kątów trójkąta wynoszą 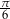 i
i 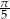 . Oblicz miarę trzeciego kąta. Odpowiedź podaj w stopniach.
. Oblicz miarę trzeciego kąta. Odpowiedź podaj w stopniach.
Dwusieczna kąta 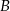 trójkąta
trójkąta 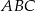 przecina bok
przecina bok 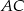 w punkcie
w punkcie 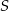 , a dwusieczna kąta
, a dwusieczna kąta 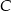 przecina bok
przecina bok 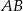 w punkcie
w punkcie 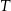 . Dwusieczne przecinają się w punkcie
. Dwusieczne przecinają się w punkcie 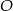 . Znajdź miarę kąta
. Znajdź miarę kąta 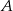 , jeżeli wiadomo, że na czworokącie
, jeżeli wiadomo, że na czworokącie 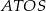 można opisać okrąg.
można opisać okrąg.
Boki trójkąta mają długości 4, 8 i 10.
- Oblicz cosinus i tangens kąta leżącego naprzeciwko najkrótszego boku.
- Oblicz długość środkowej poprowadzonej do najdłuższego boku.
Jeden z kątów trójkąta jest trzy razy większy od mniejszego z dwóch pozostałych kątów, które różnią się o 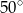 . Oblicz kąty tego trójkąta.
. Oblicz kąty tego trójkąta.
Jeden z kątów trójkąta jest trzy razy większy od drugiego oraz o 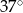 większy od trzeciego kąta. Oblicz miary wszystkich kątów tego trójkąta.
większy od trzeciego kąta. Oblicz miary wszystkich kątów tego trójkąta.
Jeden z kątów trójkąta jest cztery razy mniejszy od mniejszego z dwóch pozostałych kątów, które różnią się o 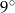 . Oblicz kąty tego trójkąta.
. Oblicz kąty tego trójkąta.
Jeden z kątów trójkąta jest cztery razy większy od drugiego oraz o 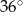 mniejszy od trzeciego kąta. Oblicz miary wszystkich kątów tego trójkąta.
mniejszy od trzeciego kąta. Oblicz miary wszystkich kątów tego trójkąta.
Długości boków trójkąta są w stosunku 2 : 3 : 4. Oblicz wartość wyrażenia
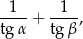
gdzie  oznacza największy, a
oznacza największy, a 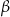 najmniejszy kąt tego trójkąta.
najmniejszy kąt tego trójkąta.
Dany jest trójkąt o bokach długości 1,  , 2. Oblicz cosinus i sinus kąta leżącego naprzeciw najkrótszego boku tego trójkąta.
, 2. Oblicz cosinus i sinus kąta leżącego naprzeciw najkrótszego boku tego trójkąta.
Kąty 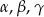 trójkąta
trójkąta 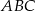 spełniają zależność
spełniają zależność
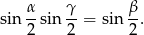
Oblicz wartość wyrażenia 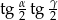 .
.
W trójkącie 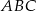 , w którym
, w którym 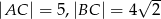 i
i 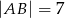 na boku
na boku 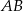 wybrano taki punkt
wybrano taki punkt 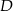 , że
, że 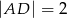 . Oblicz sinus kąta
. Oblicz sinus kąta 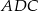 .
.
W trójkącie 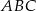 mamy dane
mamy dane 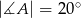 oraz
oraz 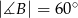 . Punkt
. Punkt 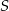 jest środkiem okręgu opisanego na tym trójkącie. Oblicz miary kątów
jest środkiem okręgu opisanego na tym trójkącie. Oblicz miary kątów 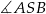 ,
, 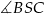 i
i 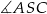 .
.
Dane są miary łukowe dwóch kątów trójkąta: 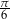 i
i 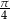 . Wyznacz miarę trzeciego kąta w stopniach i radianach.
. Wyznacz miarę trzeciego kąta w stopniach i radianach.
Dane są miary łukowe dwóch kątów trójkąta: 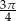 i
i 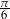 . Wyznacz miarę trzeciego kąta w stopniach i radianach.
. Wyznacz miarę trzeciego kąta w stopniach i radianach.
Dane są miary łukowe dwóch kątów trójkąta: 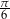 i
i 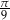 . Wyznacz miarę trzeciego kąta w stopniach i radianach.
. Wyznacz miarę trzeciego kąta w stopniach i radianach.
Dane są miary łukowe dwóch kątów trójkąta: 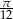 i
i 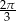 . Wyznacz miarę trzeciego kąta w stopniach i radianach.
. Wyznacz miarę trzeciego kąta w stopniach i radianach.

